蓝桥杯 试题 历届试题 最大子阵 前缀和

问题描述

　　给定一个n*m的矩阵A，求A中的一个非空子矩阵，使这个子矩阵中的元素和最大。

　　其中，A的子矩阵指在A中行和列均连续的一块。

输入格式

　　输入的第一行包含两个整数n, m，分别表示矩阵A的行数和列数。
　　接下来n行，每行m个整数，表示矩阵A。

输出格式

　　输出一行，包含一个整数，表示A中最大的子矩阵中的元素和。

样例输入

3 3
-1 -4 3
3 4 -1
-5 -2 8

样例输出

10

样例说明

　　取最后一列，和为10。

数据规模和约定

　　对于50%的数据，1<=n, m<=50；
　　对于100%的数据，1<=n, m<=500，A中每个元素的绝对值不超过5000。

---

解题思路：前缀和是一种预处理，可以降低求区间和的时间。

---

 一维前缀和 : sum[ i ] : a[ 1 ] + a[ 2 ] + ... + a[ i ] //数组a [ ] 下标从1开始。区间 [ L, R ]的和 = sum[ R ] - sum[ L-1 ] 

---

二维前缀和 sum[ i ][ j ] : 下标( i', j' )<=( i, j ) 的子矩阵和

　　•二维前缀和的计算：

　

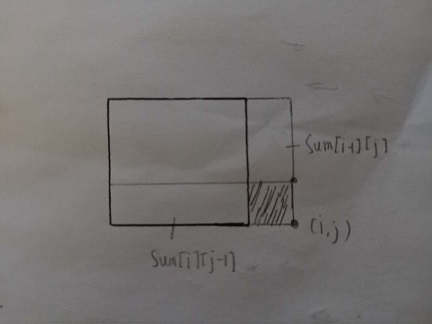
由图可以知道大矩形的和 = 两个相邻矩形和 - 重合部分 + 阴影部分矩形，用代码表示即

    for(int i=1; i<=n; i++)
    {
        for(int j=1; j<=m; j++)
        {
            Sum[i][j] = Sum[i-1][j] + Sum[i][j-1] + A[i][j] - Sum[i-1][j-1];    
        }    
    }

时间复杂度O(n^4)的解法：

有了二维前缀和，就可以遍历所以矩形的左上端点和右下端点，找到最大的矩形和。

int res = -INF;
for(int x1=0; x1<n; x1++)
    {
        for(int y1=0; y1<m; y1++)
        {
            for(int x2=x1+1; x2<=n; x2++)
            {
                for(int y2=y1+1; y2<=m; y2++)
                {
                    int t = Sum[x2][y2] - Sum[x1][y2] - Sum[x2][y1] + Sum[x1][y1];//矩形和 画张图就可以理解了
                    res = res>t ? res : t;
                }
            }
        }
    }    

但用这个方法提交后之后60分。

---

时间复杂度下降为O( n^3 )的解法。

为了更好理解二维最大和矩阵解法，首先看一维怎么计算。即求一维连续序列最大区间和。

贪心：遍历 sum [ R ] ,每一步都取最小的 sum[ L-1 ] , 求差值更新res的值。

int Min = 0 , res = -INF;
for(int i=1; i<=n; i++ ){
　  Min = min( Min, sum[ L-1 ]);
    res = max( res, sum[ R ] - Min );                  
}

二维最大区间和：

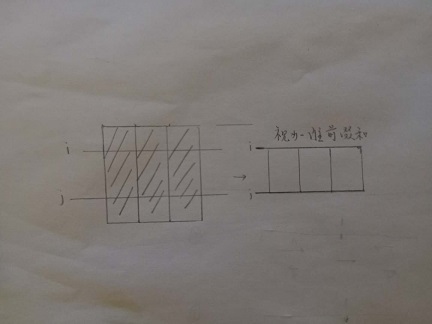
先求每一列的一维区间和，再遍历行号(0 - n ) , 这时把 行号为 i - j 的视为一维区间，再用上面的方法求最大值。

//代码实现

#include<cstdio>
#include<algorithm>
using namespace std;

const int Max_N = 500;
const int Max_M = 500;
const int INF = 100000;

//输入
int n,m;
int A[Max_N+1][Max_M+1];

int f[Max_N+1][Max_M+1];//求一列的前缀和
int sum[Max_N+1]; //求一维最大区间和的方法

void solve()
{
    for(int i=1; i<=n; i++)
    {
        for(int j=1; j<=m; j++){
            f[i][j] = f[i-1][j] + A[i][j];//一列前缀和 
        }    
    }    
    
    int res = -INF;
    for(int i=0; i<n; i++)
    {
        for(int j=i+1; j<=n; j++)//遍历行号 
        {
            for(int k=1; k<=m; k++)//先求一维前缀和 
            {
                sum[k] = f[j][k] - f[i][k] + sum[k-1];
            }
            
            int Min = 0;
            for(int k=1; k<=m; k++)//求一维最大区间和 
            {
                Min = min( Min,sum[k-1] );
                res = max( res,sum[k]-Min );
            }
            
        }
    }
    printf("%d
",res);
} 

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1; i<=n; i++){
        for(int j=1; j<=m; j++){
            scanf("%d",&A[i][j]);
        }
    }
    
    solve();
    
    return 0;
}