0.PTA得分截图

1.本周学习总结
1.1 总结线性表内容
1.顺序表结构体定义、顺序表插入、删除的代码操作
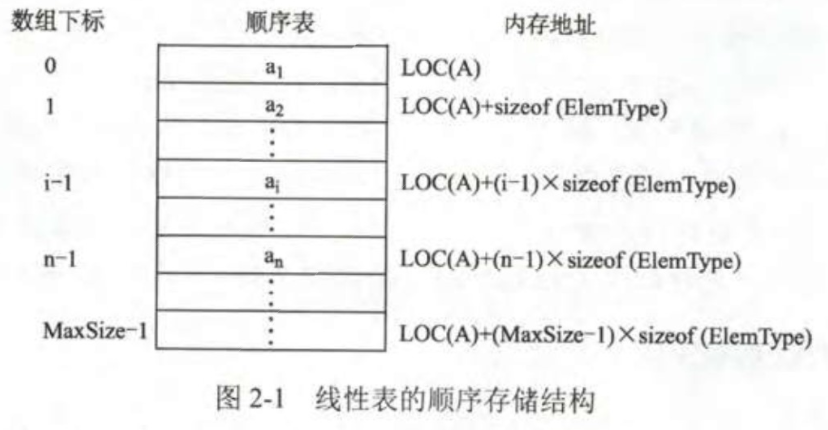
顺序表的定义:
线性表的顺序存储又称为顺序表。
它用一组地址连续的存储单元,依次存储线性表中的数据元素,从而使得逻辑上相邻的两个元素在物理位置上也相邻。
第 1 个元素存储在线性表的起始位置,第 i 个元素的存储位置后面紧接着存储的是第 i+1 个元素。
因此,顺序表的特点是表中元素的逻辑顺序与其物理顺序相同。
顺序表结构体的定义:typedef int ElemType即是定义数据元素类型,可以适应更多类型;
typedef struct的内容就是定义了定义顺序表类型,只是定义了一个类型,而不是变量;
顺序表结构的定义,对于在代码的后续操作起着关键性作用,所以在结构体的定义中要仔细。

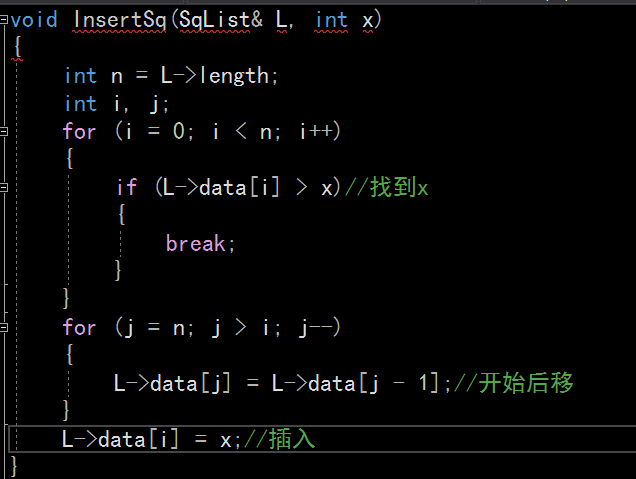
顺序表插入、删除的代码操作:顺序表的插入和删除操作,在顺序表开始寻找到相对性的数值,
就开始执行操作。删除操作针对于区间删除来说,先从第一个for循环开始执行,定义三个变量,
找到重复元素就开始删除操作。顺序表的插入删除都是要遍历链表,找到相对应的元素进行操作。

2.链表结构体定义、头插法、尾插法、链表插入、删除操作
链表结构体的定义:对于单链表而言,先定义的一个结构体用来描述单链表的结点。从这个结构
定义中,我们知道,结点由存放数据元素的数据域存放后继结点地址的指针域组成。对于ElemType
就是定义一个结构体成员,struct Node* next的语句对于链表的结点指向的操作,其中每个数据
分为两部分,一部分是数据存储的位置,称为数据域,另外指针所存储的地方,称为指针域。

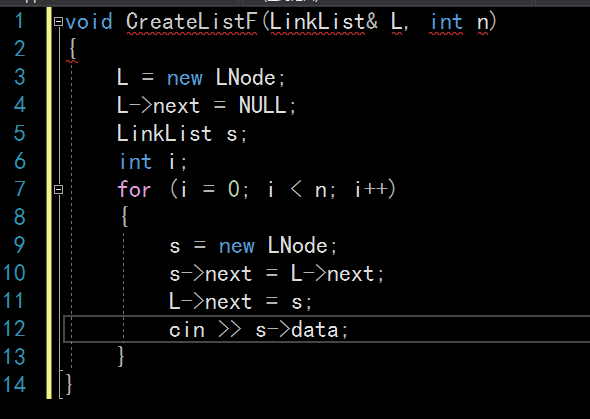
头插法建链表操作:从一个空表开始,重复读入数据,生成新结点,将读入数据存放到新结点的数据域中,
然后将新结点插入到当前链表的表头结点之后,直至读入结束标志为止。首先对于链表L申请空间,再
L->next=NULL指向空指针,LinkList s,申请新的链表s,用s来保留L的->next,再通过s插入数据
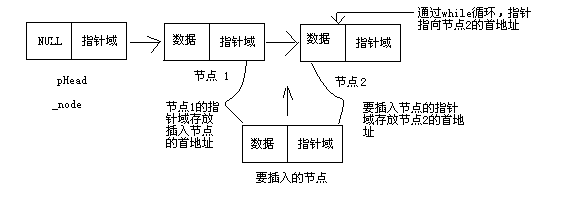
尾插法建链表:将新结点插到当前链表的表尾上,增加一个尾指针,使之指向当前链表的表尾。
尾插法建链表比从头插法建链表操作多一个尾结点tail,用tail->next尾部插入数据

链表插入:
链表删除:

3.有序表,尤其有序单链表数据插入、删除,有序表合并
有序单链表数据插入,删除:所谓有序表,其中所有元素以递增或者递减方式有序排列;有序表
包含于线性表;有序表和线性表中元素之间的逻辑关系相同,其区别是运算实现的不同。
有序单链表插入:
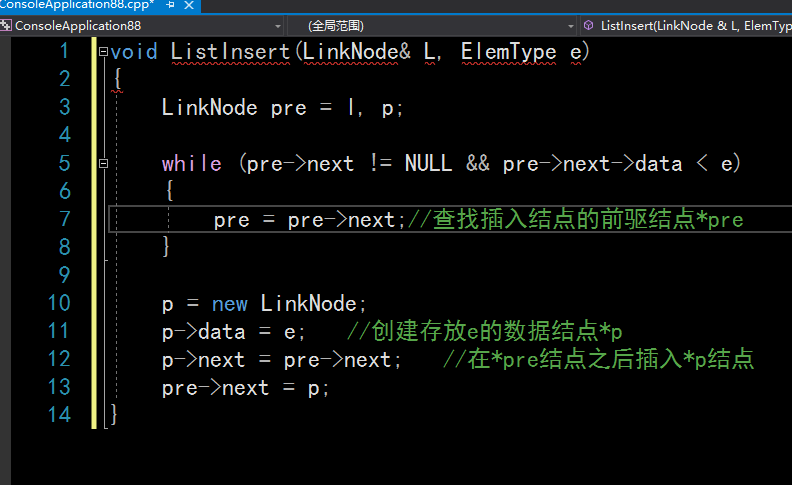
有序单链表删除:

有序表合并:
伪代码:
新建顺序表LC;
i表示LA的下标,j表示LB的下标
while(i<LA.length&&j<LB.length)
{
if(LA->data[i]<LB->data[j]) 则LC中插入元素LA->data[i],i++;
else 插入元素LB->data[j],j++
LC数组长度加1;
}
查看LA或者LB是否扫描完毕,没扫描玩把剩余元素复制插入LC
归并(没有显示重复数据)
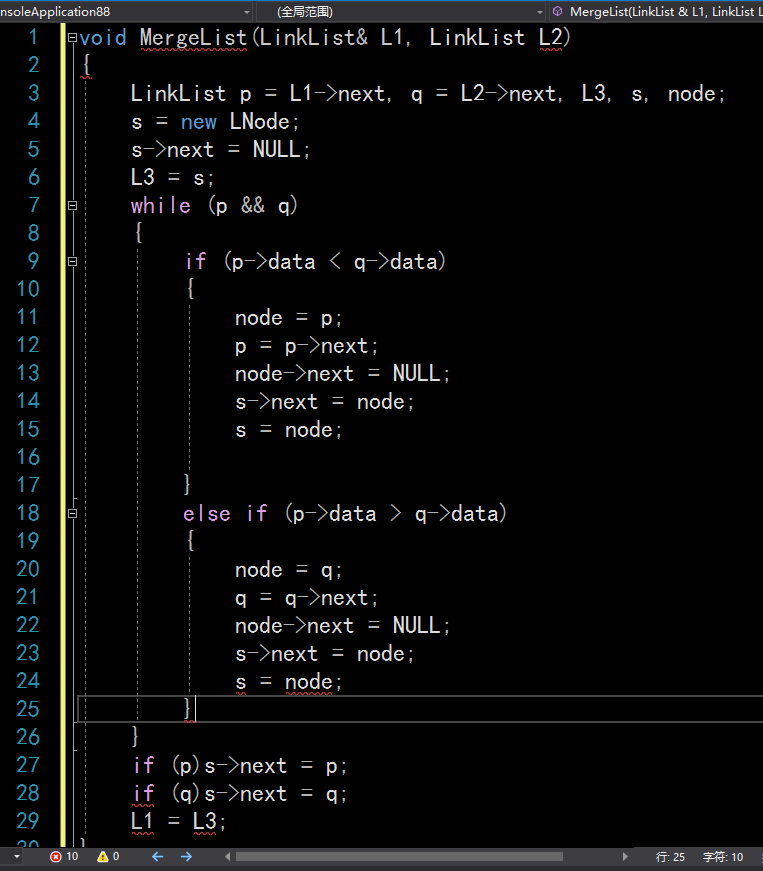
4. 循环链表、双链表结构特点
双链表:双链表每个节点有2个指针域。一个指向后续节点,一个指向前驱结点。

类型定义:
typedef struct DNode { //定义双链表结点类型
ElemType data; //数据域
struct DNode *prior,*next; //前驱和后继指针
} DNode *DLinklist;
双链表中的插入结点操作语句:
s->next=p->next;
p->next->prior=s;
s->prior=p;
p->next=s;
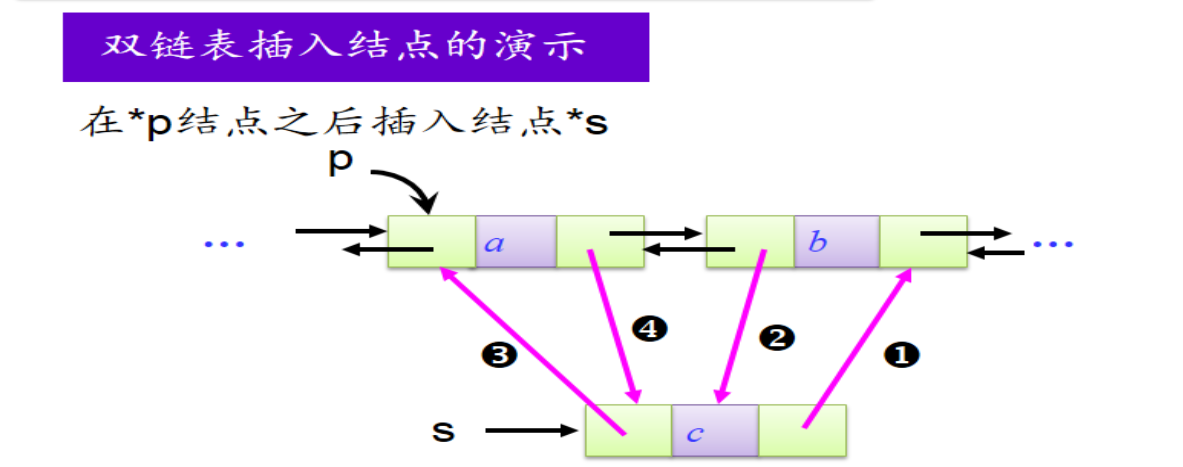
双链表删除结点操作:
p->next->next->prior=p;
p->next=p->next->next;

循环链表:循环链表是另一种形式的链式存储结构形式。将表中尾结点的指针域改为
指向表头结点,整个链表形成一个环。由此从表中任意节点出发均可以找到链表中其他
节点。循环双链表与非循环相比,链表中没有空指针域;p所指结点为尾结点的条件:
p->next==L;一步操作既可以找到尾结点


5.线性表特点
表中元素的个数有限。
表中元素具有逻辑上的顺序性,在序列中各元素排序有其先后次序。
表中元素都是数据元素,每一个元素都是单个元素。
表中元素的数据类型相同,这意味着每一个元素占有相同大小的存储空间。
表中元素具有抽象性。即仅讨论元素间的逻辑关系,不考虑元素究竟表示什么内容。
线性表是一种逻辑结构,表示元素之间一对一的相邻关系。
顺序表和链表是指存储结构,两者属于不同层面的概念
6.线性表基本操作
InitList(&L):初始化表。构造一个空的线性表。
Length(L):求表长。返回线性表 L 的长度,即 L 中数据元素的个数。
LocateElem(L,e):按值查找操作。在表 L 中査找具有给定关键字值的元素。
GetElem(L,i):按位査找操作。获取表 L 中第 i 个位置的元素的值。
ListInsert(&L,i,e):插入操作。在表 L 中第 i 个位置上插入指定元素 e。
ListDelete(&L,i,&e):删除操作。删除表 L 中第 i 个位置的元素,并用 e 返回删除元素的值。
PrintList(L):输出操作。按前后顺序输出线性表 L 的所有元素值。
isEmpty(L):判空操作。若 L 为空表,则返回true,否则返回false。
DestroyList(&L):销毁操作。销毁线性表,并释放线性表 L 所占用的内存空间。
1.2谈谈你对线性表的认识及学习体会。
线性表因存储结构的不同,分为顺序表和链表。顺序表适合于查找、修改第i个结点的值(其时间复杂度为O(1)),
但插入或者删除结点就要每次都移动数组,比较麻烦。链表适合用于插入删除某个结点,比较灵活,也比较绕。
在打pta的过程中,由于大多数都没有注意到一些基础函数,在打编程题的时候就一直各种错误,尤其是初始化链表,
一直出现段错误,在链表中还要注意不能出现野指针,所以要提高正确率,最好要学会背代码....
2.PTA实验作业
2.1.题目1:有序链表合并
2.1.1代码截图


2.1.2本题PTA提交列表说明。

Q1:最开始的时候出现段错误。
A1:没有对L3进行初始化
Q2:中间部分出现部分正确
A2:因为在复制上一段代码的时候,在重复数据出现时候忘记p=p->next
2.2.题目2:链表倒数第m个数
2.2.1代码截图
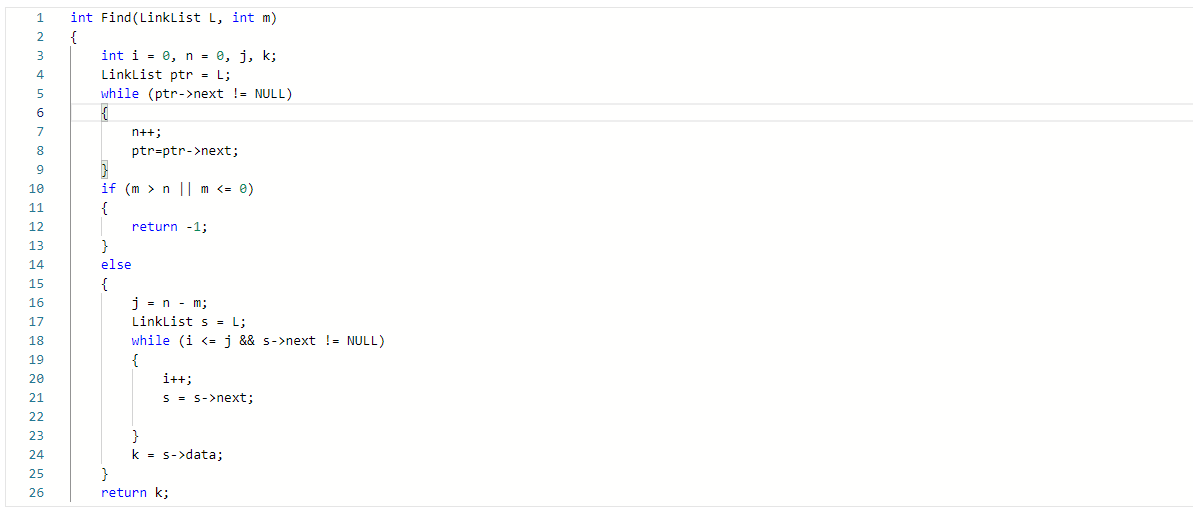
2.2.2本题PTA提交列表说明

Q1:编译错误从VS转移代码的时候最后漏掉}
A1:加上}
Q2:一开始的运行超时是while里面忘记让用来遍历的pre指针往后移了,导致while出不来,就运行超时了。
A2:添加了一个pre=pre->next
Q3:编译错误就是承接上一个错误,添加了pre=pre->next,变量时ptr
A3:pre=pre->next改成ptr=ptr->next
2.3.题目3:一元多项式的乘法与加法运算
2.3.1代码截图
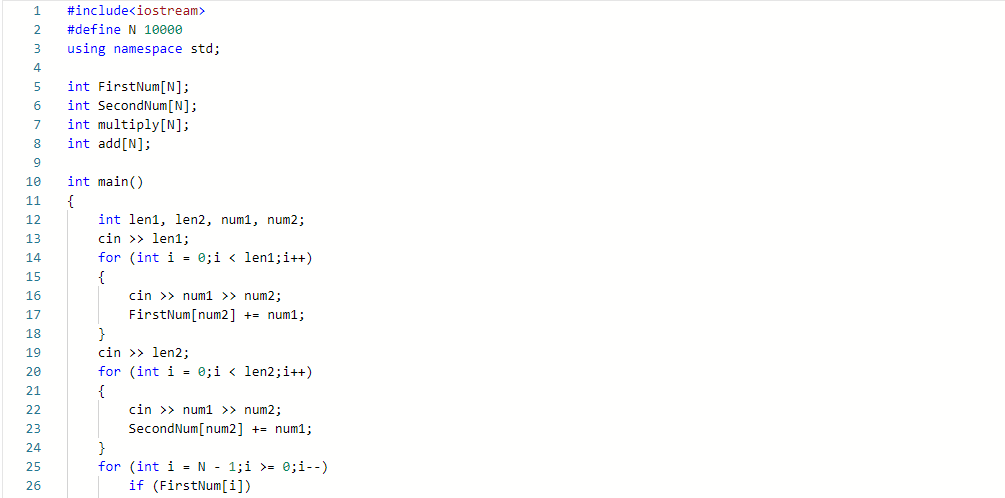


2.3.2本题PTA提交列表说明

Q1:编译错误
A1:加逗号
Q2:段错误,在for循环发生错误,for (int i = N - 1;i >= 0;i++)编写错误
A2:改为for (int i = N - 1;i >= 0;i--)
Q3:部分正确,就是答案的格式错误
A3:结尾改为cout << "0 0"
3.阅读代码
3.1 题目及解题代码
题目:

解题代码:
#include <iostream>
#include <stdlib.h>
using namespace std;
# define MAXSIZE 1000
typedef int ElemType;
typedef struct {
ElemType data[MAXSIZE];
int length;
}Vector;
Vector* CircleLeftMove(Vector* v, int p) {
Vector* v_temp = (Vector*)malloc(sizeof(Vector));
v_temp->length = p;
int i;
for (i = 0; i < v->length; i++) {
v_temp->data[i] = v->data[i];
v->data[i] = v->data[i + p];
}
for (i = 0; i < p; i++) {
v->data[v->length - p + i] = v_temp->data[i];
}
return v;
}
3.1.1 该题的设计思路
借助辅助数组v_temp存储原表的前p个元素,并把原顺序表中p之后的元素顺序前移,
然后将v_temp中暂存的p个数的元素依次放回到原顺序表的后续单元。
时间复杂度为O(n)
空间复杂度为O (p)
3.1.2 该题的伪代码
定义data的数组空间大小,链表长度
申请v_temp空间
v_temp->length = p存储前p个元素
for(原顺序表中p之后的元素顺序前移)
v_temp中暂存的p个数的元素依次放回到原顺序表的后续单元;
return v;
3.1.3 运行结果

3.1.4分析该题目解题优势及难点。
1.使用静态分配的方式创建一维数组:数组的大小和空间固定,一旦占满再加入新的数据会导致程序崩溃
2.运用辅助数组v_temp来存储元素,再进行前移再放回,思路很清晰
3.2题目及解题代码
题目:

解题代码:
#include <iostream>
#include <stdlib.h>
using namespace std;
# define MAXSIZE 1000
typedef int ElemType;
typedef struct {
ElemType data[MAXSIZE];
int length;
}Vector;
int getMidByCompare(Vector v1, Vector v2) {
int num1 = 0, num2 = 0;
int end1 = v1.length - 1;
int end2 = v2.length - 1;
int mid1, mid2;
while (num1 != end1 || num2 != end2) {
mid1 = (num1 + end1) / 2;
mid2 = (num2 + end2) / 2;
if (v1.data[mid1] == v2.data[mid2]) {
return v1.data[mid1];
}
if (v1.data[mid1] < v2.data[mid2]) {
if ((num1 + end1) % 2 == 0) {
num1 = mid1;
end2 = mid2;
}
else {
num1 = mid1 + 1;
end2 = mid2;
}
}
else {
if ((num2 + end2) % 2 == 0) {
end1 = mid1;
num2 = mid2;
}
else {
end1 = mid1;
num2 = mid2 + 1;
}
}
}
return v1.data[num1] < v2.data[num2] ? v1.data[num1] : v2.data[num2];
}
3.2.1该题的设计思路
1.若v1.data[mid1] == v2.data[mid2],则mid1和mid2即为所求中位数,立即返回。
2.若v1.data[mid1] < v2.data[mid2]2,则序列1中比mid1还要小数必不可能为所求中位数,故舍弃序列1中较小的一半;同理,这时也要舍弃序列2中较大的一半。
3.若v1.data[mid1] > v2.data[mid2], 则舍弃序列1中大于mid1的数,同时也要舍弃序列2中较小的一半,直到逻辑上的序列只含一个元素时,较小者即为所求中位数。
4.时间复杂度:O(log2n)。
5.空间复杂度:O(1)。
3.2.2该题的伪代码
定义data的数组空间大小,链表长度
int num1,num2;
num结点始终指向序列中的第一个元素的下标
定义end结点始终指向序列中的最后一个元素的下标
int mid1,mid2;
while(还没找到最后一个元素循环)
{
找到中位数下标;
if(相等) return ;
if(v1.data[mid1] < v2.data[mid2])
{
if(v1的元素个数为奇数) 舍弃序列1中位数前的元素;
else 弃序列1中位数及中位数前的元素;
}
else 序列1的中位数大于序列2的中位数
{
if(v2的元素个数为奇数) 舍弃序列1中比中位数大的元素;
else 舍弃序列2的中位数及比中位数小的元素 ;
}
}
return v1.data[num1] < v2.data[num2] ? v1.data[num1] : v2.data[num2];
3.2.3运行结果

3.2.4分析该题目解题优势及难点。
该题要找出中位数,先用了num来指向序列中的第一个元素的下标 ,和end指向序列中的最后
一个元素的下标 ;感觉看起来还是有点麻烦,不是很能懂;难点在于找到序列1和2对比,
还要再舍弃。