一看到“2D矩阵”这个高大上的名词,有的同学可能会有种畏惧感,“矩阵”,看起来好高深的样子,我还是看点简单的吧。其实本文就很简单,你只需要有一点点css3 transform的基础就好。
没有前戏,直奔主题
2D矩阵指的是元素在2D平面内发生诸如缩放、平移、旋转、拉伸四种变化,在css3中对应4个方法分别是scale()、translate()、rotate()和skew(),可以说这4个方法是css3矩阵matrix的快捷方式,因为这4个方法本质都是由matrix实现的。类似地,在canvas中,与前3种变化对应的3个方法分别是scale()、translate()、rotate(),canvas对象没有skew()方法。css3中的矩阵和canvas矩阵原理是相通的,所以这里只说css3的矩阵matrix,两者有一些区别,后面会说。
matrix方法有六个参数matrix(a, b, c, d, x, y),六个参数默认值是matrix(1, 0, 0, 1, 0, 0),这六个参数分别控制不同的变换
a 水平缩放
b 水平拉伸
c 垂直拉伸
d 垂直缩放
x 水平位移
y 垂直位移
可以运行下面的demo,改动对应的参数查看效果
如果把以上css3的4个方法还原成矩阵的写法,它们是这样的:
- 缩放:scale(sx, sy) 等同于 matrix(sx, 0, 0, sy, 0, 0);
- 平移:translate(tx, ty) 等同于 matrix(1, 0, 0, 1, tx, ty);
- 旋转:rotate(deg) 等同于 matrix(cos(deg), sin(deg), -sin(deg), cos(deg), 0, 0);
- 拉伸:skew(degx, degy) 等同于 matrix(1, tan(degy), tan(degx), 1, 0, 0);
一目了然,matrix原始写法看起来更复杂一些,大家一般使用左边的快捷方式就好了。
计算变换后的transform-origin
其实矩阵基本上就上面这些内容,网上大部分介绍矩阵的教程一般都会搬出下面这张图来吓唬人
图1:

a c e分别和x y 1相乘并相加得出结果x' = ax + cy + e;
b d f分别和x y 1相乘并相加得出结果y' = bx + dy + f;
其中的x y是元素变换之前的中心点,即transform-origin的值,x' y'是元素变换之后的transform-origin值。
假设一个元素的中心点为100,100,将该元素向右平移200px,向下平移100px后,中心点坐标为:
x' = ax + cy + e = 1*100 + 0*100 + 200 = 300
y' = 0*100 + 1*100 + 100 = 200
平移后的中心点坐标为300,200
图2:
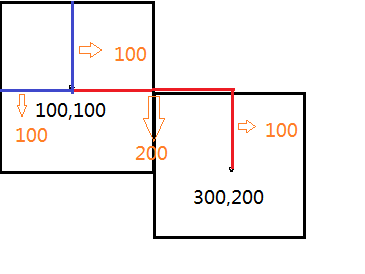
图1的作用仅仅是告诉我们如何计算元素变换后的中心点,没什么特别的。
css3 matrix和canvas transform的区别
大家都知道css3 transform-origin默认是元素的中点,css3旋转就是绕着这个点转动,而canvas的transform的rotate方法是默认绕着canvas的原点(即左上角)旋转。
OK,以上就是2D矩阵的全部内容,对文中的公式建议自己做个demo测试一下以加深印象,否则看完一会准会忘记。
水平有限,有疏漏之处欢迎交流。
by:王美建 from http://www.cnblogs.com/wangmeijian/p/4713722.html转载注明出处。