实现平衡二叉树后接着实现红黑树,红黑树接近平衡的二叉树,插入,删除函数跟平衡二叉树一样,只是平衡函数不同,平衡二叉树严格按照子树高度差,使最长路径-最短路径=0/1;
1,而红黑树的特性:
(1) 每个节点或者是黑色,或者是红色。
(2) 根节点是黑色。
(3) 每个叶子节点是黑色。 [注意:这里叶子节点,是指为空的叶子节点!]
(4) 如果一个节点是红色的,则它的子节点必须是黑色的。
(5) 从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
是通过两个红色节点不能相邻,而每条路径上的黑色点数要相同,所要求的结果就是:
使最长路径不会超过最短路经两倍,如图:右边路径有4个节点,左边路径两个;节点9后面不能再有节点了,添加红违反特性(4),添加黑违法特性(5);
(红色节点就是用来补充在 黑色节点之间只控制每条路径黑色节点相同即达到平衡,来减少平衡二叉树,频繁的平衡操作)
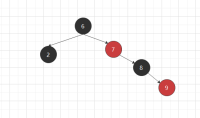
2,红黑树的平衡
- 插入和删除函数和平衡二叉树一样。这里就不说了,详情看前面博客
- 红黑树的插入节点默认是红色的,
2.1,插入后平衡
- 插入节点要看叔叔脸色(颜色),比如红黑树就是一个家族,平衡操作就是分遗产,每条路径就相当于每个小户,遗产按男丁(黑节点)分,又要每户平均,当父节点,生孩子(添加节点)
- 要与叔叔们平衡,不均衡的时候调色,(过继男孩??),233,这个比喻有点牵强,233但并没有重男轻女的意思!!!。
①如果树空,根结点指向新节点,颜色涂黑
②如果插在黑色节点后面,不需要平衡,因为不影响红黑树的特性(红色节点就是用来补充再 黑色节点间来减少平衡二叉树,频繁平衡操作的)
③如果要插入的父节点是红色,这里违反了特性(3)需要进行平衡,重新上色:
https://www.jianshu.com/p/96e652ccf720这篇博客讲的很清楚,
- 因为父节点是红色,有因为根节点是黑色,所以父节点肯定还有父节点,即祖父节点,插入的时候要根据,父节点和叔叔节点(祖父的另一个节点,即父节点的兄弟节点)
- 来判定平衡操作
- G-gradpa ,F-fathr, U-uncle, NEW-新增节点 黑色表示黑节点,灰色表示可红可黑,暗红表示红节点,亮红表示添加/变动节点或者当前节点
③.1 父红,叔红: 将父节点和叔叔节点涂黑,祖父节点涂红,以祖父节点为New回溯平衡,为什么需要回溯,
是因为图中l路径新增了黑节点,而r路径相对就少了黑节点,依次往后类推直到根节点。(对称的情况类似)


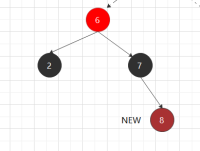
对称: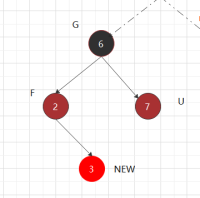

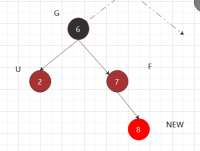
③.2 父红(祖父必黑),叔黑:
③.2.1 新增和父节同边 -以祖父节点右旋;然后将F涂黑,将G涂红。---使原有路径如(U,?,new)所经过的黑节点数不变
不需要回溯。 (对称操作相反)。
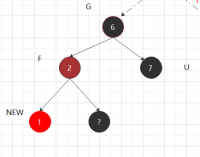
 对称
对称 
③.2.2 新增和父节不同边 先以父节点左旋,以P为新的new节点 ,进入③.2.1状态
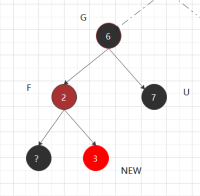
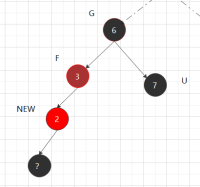 对称处理相反,先右旋再进入对应③.2.1状态:
对称处理相反,先右旋再进入对应③.2.1状态:
插入平衡函数:

1 /**插入后修改 2 * 父节点为黑-不需要修改 3 * 父节点为红,则其肯定有黑祖父节点(其父节点肯定不为根节点,因为根节点为黑) 4 * ①叔叔为红-爷爷肯定黑 5 * ②叔叔为黑,他是父节点的右儿子 6 * ③叔叔黑,他是父节点的左儿子 7 */ 8 9 public void fixAfterInseart(Node newNode){ 10 while (newNode.father!=null&&newNode.father.color==true){ 11 //System.out.println("in fixAfterInsert"); 12 //父节点为红,必有祖父节点 13 Node father =newNode.father; 14 Node grandpa=newNode.father.father; 15 Node uncle; 16 if(father==grandpa.lchild){ 17 uncle=grandpa.rchild; 18 //①叔叔为红 19 if(isRed(uncle)){ 20 //System.out.println("fixAfterInsert case1"); 21 uncle.color=false; 22 father.color=false; 23 grandpa.color=true; 24 newNode=grandpa; 25 continue; 26 } 27 //叔黑, 28 //②当前节点为右孩子 29 if(newNode==father.rchild){ 30 //System.out.println("fixAfterInsert case2"); 31 newNode=father; 32 leftRotation(newNode); 33 Node p=father; 34 father=newNode; 35 newNode=p; 36 //②执行完触发③ 37 } 38 //System.out.println("fixAfterInsert case3"); 39 //③当前节点为左孩子 40 father.color=false; 41 grandpa.color=true; 42 rightRotation(grandpa); 43 //System.out.println("afterfix case3 newNode: "+newNode.data); 44 45 } 46 //对称的情况 47 else{ 48 uncle=grandpa.lchild; 49 if(isRed(uncle)==true){ 50 //System.out.println("fixAfterInsert case4"); 51 uncle.color=false; 52 father.color=false; 53 grandpa.color=true; 54 newNode=grandpa; 55 continue; 56 } 57 if(newNode==father.lchild){ 58 //System.out.println("fixAfterInsert case5"); 59 //newNode=father; 60 rightRotation(father); 61 Node p=father; 62 father=newNode; 63 newNode=p; 64 //执行完5,会触发6 65 } 66 //System.out.println("fixAfterInsert case6"); 67 father.color=false; 68 grandpa.color=true; 69 leftRotation(grandpa); 70 } 71 72 73 } 74 //根节点黑化 75 this.root.color=false; 76 //System.out.println("afterfixinseart newNode: "+newNode.data); 77 }
2.2 删除后平衡:
2.2.1将删除平衡之前先讲一下删除函数,也就是平衡二叉树删除函数,
[1],待删节点无子节点,直接待删节点的父节点的对应子树为空即可,若是红黑树,D若是红节点,不需要平衡,若是黑节点,则以D的子节点(null)为new节点回溯遍历平衡调色
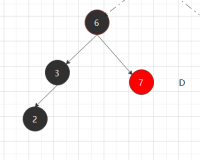
[2]待删节点有子节点(子树),我实现平衡二叉树用的是若待删节点有右子树,就从右子树上找最小值替代,若无右子树则找左子树最大值代替
[2.1]如图以左子树最大值为例,用m节点的值替换被删节点的值,再由m的左子数根节点(可能为空)上来补位,因为是左子树最大值,不可能有右节点,也就是相当于
删除的其实是替代节点m(D只是把值换一下,指针关系没有变)。因为红黑树用的就是平衡二叉树的删除函数,所以在红黑树中,如果m是红节点,则不需要平衡,
删除红节点不影响红黑树特性,若m是黑节点,则ml,及其子树路径上就少了一个黑节点,需要以ml为new节点回溯遍历,平衡调色。

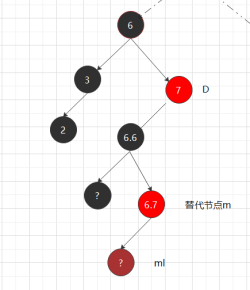
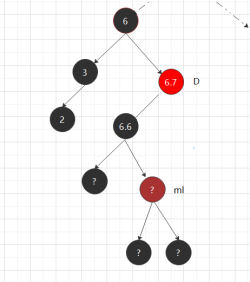
[2.2]有右子树的情况:

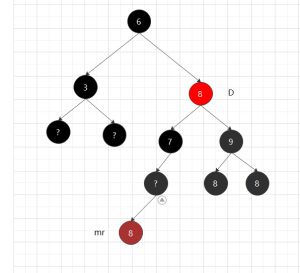
2.2.2 删除后平衡:
删除节点是要看兄弟节点的脸色(颜色),可以理解为,子节点要断绝与父亲的关系(假设赡养责任也断了)要看他的兄弟(和他一起赡养父亲)的脸色
- 如果删除的是 红节点,则不影响红黑树特性,不需要平衡,
- 删除黑节点,并补位后(补充的可能是null),以补充节点所在位置ml开始,回溯遍历,平衡调色。
- B-brother BL-兄弟左孩子 BR-兄弟右孩子 F-father new(新增/变动 节点)
①兄红(其子比黑,父必黑) ----- ( r路径上,删除了一个黑节点,记为-1,) 以F右旋,BF换色,---进入②.1.1 兄黑,兄子全黑 父黑


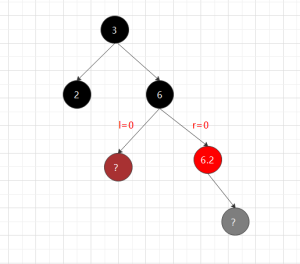
对称: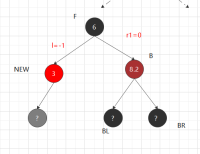 处理相反
处理相反
②兄黑
②.1 兄黑,兄子全黑
②.1.1 兄黑,兄子全黑 父黑 兄变红,以父节点为new回溯,兄变红,两条路径都少了黑节点,以父节点回溯,调整父节点的兄弟节点。
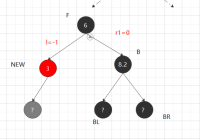
 对称
对称
②.1.2 兄黑,兄子全黑 父红 兄弟涂红,父涂黑-不用递归 --r,与l路径上黑节点与其他相同
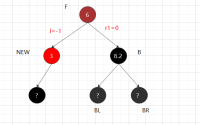
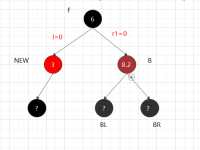
对称: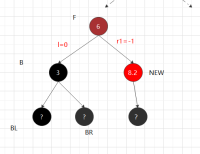
②.2 兄黑,兄子不全黑
②.2.1,兄黑,兄子靠外侧的红,内侧颜色任意 B涂父节点颜色,父节点涂黑,以父节点左旋,B靠外的节点涂黑,
平衡结束后各子树,黑节点个数与其他相同,不用递归
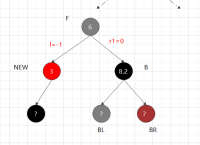
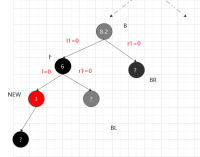 对称:
对称: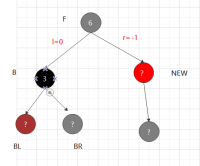
②.2.2,兄黑,兄子靠内侧的红,外侧颜色黑 先以兄弟节点,右旋,进入②.2.1 兄黑,兄子靠外侧的红,内侧颜色任意
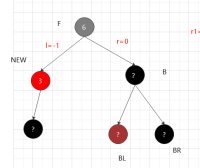
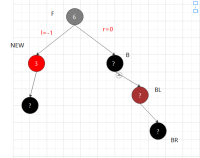 对称:
对称:
删除修正代码:

1 /**删除后修改 2 * //因为我自己实现二叉搜索树删除节点时,是用的下面规则,所以顺延过来 3 * 4 * ①删除节点无子节点,不需要修改 5 * 6 * ②有右子树-用右子树最小值X节点替换被删节点(保留删除节点的颜色和指针,只对值替换,其实只动了替换节点X那里,动了之后新顶替x.child上来一个或者为null为X,以此回溯,调色) 7 * ,只有替换节点X是黑色才需要调色: 8 * 因为从子树抽调一个红色节点,并不影响红黑树特性 9 * 调色节点:(X,X.father) 10 * ③只有左子树-用左子树最大值节点替换被删节点X(保留删除节点的颜色和指针,只讲值替换,其实只动了替换节点X那里,动了之后新顶替x.child上来一个或者为null为X,以此回溯,调色) 11 * ,,只有该节点X是黑色才需要调色: 12 * 因为从子树抽调一个红色节点,并不影响红黑树特性 13 * 需要调色:(X,X.father) 14 * 15 * 调色的4种情况 16 * ①兄弟节点红 17 * ②兄弟节点黑,兄弟的两个孩子也黑 18 * ③兄弟黑,兄左孩子红,右孩子黑 19 * ④兄弟黑,兄弟有孩子红,左孩子颜色任意 20 */ 21 public void fixAfterdelete(Node p,Node father){ 22 Node brother=null; 23 while((p!=this.root)){ 24 //System.out.println("顶替节点:p"+p.data); 25 System.out.println("顶替节点父节点:p"+father.data); 26 System.out.println(father.lchild==p); 27 System.out.println(father.rchild==p); 28 if(father.lchild==p){ 29 brother=father.rchild; 30 //System.out.println("brother: "+brother.data); 31 //①兄红 32 if(isRed(brother)){ 33 System.out.println("fixAfterdelete case1"); 34 brother.color=false; 35 father.color=true; 36 leftRotation(father); 37 brother=father.rchild; 38 } 39 //兄黑 40 //②兄子全黑 41 if((!isRed(brother.lchild))&&(!isRed(brother.rchild))){ 42 System.out.println("fixAfterdelete case2"); 43 brother.color=true; 44 p=father; 45 //父红,涂黑,不用回溯 46 if(father.color){ 47 father.color=false; 48 break; 49 } 50 father=father.father; 51 }//兄子不全黑, 52 else{ 53 //③兄左孩子红,有孩子黑-先右旋--进入④状态 54 if(!isRed(brother.rchild)){ 55 System.out.println("fixAfterdelete case3"); 56 brother.lchild.color=false; 57 brother.color=true; 58 rightRotation(brother); 59 brother=father.rchild; 60 } 61 //④兄右孩子红,左孩子颜色任意-左旋 62 System.out.println("fixAfterdelete case4"); 63 brother.color=father.color; 64 father.color=false; 65 brother.rchild.color=false; 66 leftRotation(father); 67 break; 68 } 69 } 70 else{ 71 brother=father.lchild; 72 //①兄红 73 if(isRed(brother)){ 74 System.out.println("fixAfterdelete case5"); 75 brother.color=false; 76 father.color=true; 77 rightRotation(father); 78 brother=father.lchild; 79 } 80 //兄黑 81 //②兄子全黑 82 if((!isRed(brother.lchild))&&(!isRed(brother.rchild))){ 83 System.out.println("fixAfterdelete case6"); 84 brother.color=true; 85 p=father; 86 //父红,涂黑,不用回溯 87 if(father.color){ 88 father.color=false; 89 break; 90 } 91 //father.color=false; 92 father=father.father; 93 //回溯 94 }//兄子不全黑, 95 else{ 96 //③兄右孩子红,左孩子黑-先右旋--进入④状态 97 if(isRed(brother.lchild)==false){ 98 System.out.println("fixAfterdelete case7"); 99 brother.lchild.color=false; 100 brother.color=true; 101 leftRotation(brother); 102 brother=father.rchild; 103 } 104 //④兄左孩子红,右孩子颜色任意-右旋 105 System.out.println("fixAfterdelete case8"); 106 brother.color=father.color; 107 father.color=false; 108 brother.lchild.color=false; 109 rightRotation(father); 110 break; 111 } 112 } 113 } 114 }
完整代码
1 /** 2 * 参考:https://www.cnblogs.com/lycroseup/p/7324229.html 3 * https://blog.csdn.net/u012149181/article/details/88789595 4 * 5 * 这个总结的最好: 6 * https://www.jianshu.com/p/96e652ccf720 7 * https://www.jianshu.com/p/84416644c080 8 * 9 * 红黑树-接近平衡的二叉树 10 * 11 * 添加,删除,调整(旋转-着色) 12 * 节点:比AVL树多一个颜色属性 13 * 14 * 主体主要还是复制AVL树---见上一篇 15 * 16 */ 17 18 import java.util.LinkedList; 19 import java.util.Queue; 20 public class RedBlackTree { 21 public class Node{ 22 private Node father=null; 23 private Node lchild=null; 24 private Node rchild=null; 25 26 private int data=Integer.MAX_VALUE; 27 private boolean color=false;//true 红 false 黑 28 29 public Node(){} 30 public Node(int data){ 31 this.data=data; 32 this.color=true;//默认红色---新增节点 33 } 34 } 35 //RedBlackTree成员变量--根节点; 36 private Node root=null; 37 38 39 /** 40 * 复制上一篇, 41 * 插入,删除后重新调整树(重新上色)做调整 42 */ 43 //是否存在 44 public boolean isExist(Node root,int data){ 45 if(root==null)//树空 46 return false; 47 if(root.data==data) 48 return true; 49 else if(data<root.data){ 50 if(root.lchild==null) 51 return false; 52 else 53 return isExist(root.lchild,data); 54 }else{ 55 if(root.rchild==null) 56 return false; 57 else 58 return isExist(root.rchild,data); 59 } 60 } 61 //插入-建树 62 public void inseart(Node root,int data){ 63 //System.out.println("now inseart "+data); 64 Node newNode=new Node(data); 65 if(isExist(root,data)){ 66 System.out.println(data+"已经存在树中"); 67 return; 68 } 69 //树空插入根节点--不用回溯,直接return 70 if(root==null){ 71 this.root=new Node(data); 72 this.root.color=false; 73 return; 74 } 75 else{ 76 //元素不能重复, 77 if(data<root.data){ 78 if(root.lchild==null){ 79 root.lchild=newNode; 80 newNode.father=root; 81 //System.out.println("newNode1: "+newNode.data); 82 //System.out.println("newNode.father: "+newNode.father.data); 83 } 84 else{ 85 inseart(root.lchild,data); 86 } 87 } 88 else{ 89 if(root.rchild==null){ 90 root.rchild=newNode; 91 newNode.father=root; 92 //System.out.println("newNode1: "+newNode.data); 93 //System.out.println("newNode.father: "+newNode.father.data); 94 }else 95 inseart(root.rchild,data); 96 } 97 } 98 //插入完了要回溯,平衡 99 //System.out.println("newNode1: "+newNode.data); 100 //System.out.println("newNode.father: "+newNode.father.data); 101 fixAfterInseart(newNode); 102 } 103 104 /**删除-复制上一篇 105 * 先实现删除最大值最小值, 106 * 107 * 删除后-平衡-重新上色 108 * 109 * 只有删除黑节点才会影响到平衡 110 */ 111 112 public void deleteMin(Node root){ 113 //空树 114 if(root==null){ 115 System.out.println("树空,无最小值"); 116 return; 117 } 118 //只有一个根节点 119 else if(root.lchild==null&&root.rchild==null){ 120 this.root=null; 121 return; 122 } 123 //根节点无左子树(删除根节点) 124 else if(root.lchild==null){ 125 this.root=root.rchild; 126 root.rchild.father=null; 127 } 128 //有左子树且非空 129 while(root.lchild!=null){ 130 root=root.lchild; 131 } 132 root.father.lchild=root.rchild; 133 if(root.rchild!=null) 134 root.rchild.father=root.father; 135 if(!root.color){ 136 // System.out.println("顶替节点: "+p.data); 137 // System.out.println("顶替节点父节点: "+p.father.data); 138 // if(p.father.rchild==null) 139 // System.out.println("候补节点: "+"空"); 140 // else 141 // System.out.println("候补节点: "+p.father.rchild.data); 142 System.out.println("触发fixAfterdelete"); 143 fixAfterdelete(root.rchild,root.father); 144 } 145 root.rchild=null; 146 //banlanceTree(root); 147 } 148 149 public void deleteMax(Node root){ 150 //空树 151 if(root==null){ 152 System.out.println("树空,无最大值"); 153 return; 154 } 155 //只有一个根节点 156 else if(root.lchild==null&&root.rchild==null){ 157 if(root.father==null) 158 this.root=null; 159 return; 160 } 161 //根节点无右子树(删除根节点) 162 else if(root.rchild==null){ 163 this.root=root.lchild; 164 root.lchild.father=null; 165 } 166 //有右子树且非空 167 else if(root.rchild!=null){ 168 while(root.rchild!=null){ 169 root=root.rchild; 170 } 171 root.father.rchild=root.lchild; 172 if(root.lchild!=null) 173 root.lchild.father=root.father; 174 } 175 if(!root.color){ 176 // System.out.println("顶替节点: "+p.data); 177 // System.out.println("顶替节点父节点: "+p.father.data); 178 // if(p.father.rchild==null) 179 // System.out.println("候补节点: "+"空"); 180 // else 181 // System.out.println("候补节点: "+p.father.rchild.data); 182 System.out.println("触发fixAfterdelete"); 183 fixAfterdelete(root.lchild,root.father); 184 } 185 root.lchild=null; 186 //banlanceTree(root); 187 } 188 189 public void delete(Node root,int data){ 190 //在树中(树非空) 191 if(!isExist(root,data)){ 192 System.out.println(data+"值不在树中"); 193 return; 194 } 195 //以下默认在树中 196 System.out.println("now delete "+data); 197 198 //只有一个节点-即删除根节点 199 if(root.lchild==null&&root.rchild==null){ 200 this.root=null; 201 return; 202 } 203 //先遍历到节点,在删除-将替换节点的值赋给该节点, 204 else{ 205 while(root.data!=data){ 206 if(data<root.data){ 207 root=root.lchild; 208 } 209 else if(data>root.data){ 210 root=root.rchild; 211 } 212 } 213 //此时root即待删除节点; 214 System.out.println("now at deletenode:"+root.data); 215 //该节点无子节点 216 if(root.lchild==null&&root.rchild==null){ 217 if(root.father.lchild==root){ 218 root.father.lchild=null; 219 } 220 else{ 221 root.father.rchild=null; 222 } 223 if(root.color==false) 224 fixAfterdelete(null,root.father); 225 } 226 //只有左子节点 227 else if(root.lchild!=null&&root.rchild==null){ 228 //拿到左子树的最大值, 229 //Node replaceNode=deleteMax(root.lchild); 230 Node p=root.lchild; 231 if(p.lchild==null&&p.rchild==null){ 232 if(p.father.lchild==p) 233 p.father.lchild=null; 234 else 235 p.father.rchild=null; 236 } 237 //根节点无右子树(删除根节点) 238 else if(p.lchild!=null&&p.rchild==null){ 239 if(p.father.lchild==p){ 240 p.father.lchild=p.lchild; 241 p.lchild.father=p.father; 242 }else { 243 p.father.rchild=p.lchild; 244 p.lchild.father=p.father; 245 } 246 } 247 //有右子树且非空 248 else if(p.rchild!=null){ 249 while(p.rchild!=null){ 250 p=p.rchild; 251 } 252 p.father.rchild=p.lchild; 253 if(p.lchild!=null) 254 p.lchild.father=p.father; 255 } 256 root.data=p.father.data; 257 System.out.println("左子树最大值: "+p.data); 258 if(!p.color){ 259 System.out.println("触发fixAfterdelete"); 260 fixAfterdelete(p,p.father); 261 } 262 p.lchild=null; 263 264 } 265 //有右子节点 266 else if(root.rchild!=null){ 267 //拿到右子树的最小值 268 //Node replaceNode=deleteMin(root.rchild); 269 Node p=root.rchild; 270 if(p.lchild==null&&p.rchild==null){ 271 System.out.println("根节点无子树"); 272 if(p.father.lchild==p) 273 p.father.lchild=null; 274 else 275 p.father.rchild=null; 276 } 277 //根节点无左子树(删除根节点) 278 else if(p.lchild==null){ 279 System.out.println("根节点无左子树"); 280 if(p.father.lchild==p){ 281 p.father.lchild=p.rchild; 282 p.rchild.father=p.father; 283 }else { 284 p.father.rchild=p.rchild; 285 p.rchild.father=p.father; 286 } 287 System.out.println("p.father"+p.father); 288 } 289 //有左子树且非空 290 else if(p.lchild!=null){ 291 System.out.println("有左子树且非空"); 292 while(p.lchild!=null){ 293 p=p.lchild; 294 } 295 p.father.lchild=p.rchild; 296 if(p.rchild!=null) 297 p.rchild.father=p.father; 298 } 299 root.data=p.data; 300 System.out.println("右子树最小值: "+p.data); 301 if(!p.color){ 302 System.out.println("顶替节点: "+p.data); 303 System.out.println("顶替节点父节点: "+p.father.data); 304 if(p.father.rchild==null) 305 System.out.println("候补节点: "+"空"); 306 else 307 System.out.println("候补节点: "+p.father.rchild.data); 308 System.out.println("触发fixAfterdelete"); 309 fixAfterdelete(p.lchild,p.father); 310 } 311 p.rchild=null; 312 } 313 } 314 } 315 316 /**辅助函数-从前一篇复制-----增加颜色属性 317 * 求树高 318 * 打印树 319 */ 320 //递归求树高-用于打印树 321 //递归 322 public int treeHeightRec(Node root){ 323 if(root==null) 324 return 0; 325 else{ 326 int a =treeHeightRec(root.lchild); 327 int b = treeHeightRec(root.rchild); 328 return (a>b)?(a+1):(b+1); 329 } 330 } 331 //打印树--233,复制前一篇的方法,如果树层数很深时,打印的比较别扭 332 public void printTree(Node root){ 333 int H=treeHeightRec(root); 334 int h=H; 335 //System.out.println("树高:"+H); 336 if(H==0) 337 System.out.println("树空,无打印"); 338 else{ 339 System.out.println("打印树:"); 340 Queue<Node> queue=new LinkedList<>(); 341 queue.add(root); 342 int height=1; 343 //记录每层孩子个数 344 int len=1; 345 while(h>0){ 346 int length=0; 347 String space=""; 348 //3+一个汉字 349 for(int i=0;i<(((Math.pow(2,H)+1)*7)/(Math.pow(2,height)+1));i++) 350 space+=" "; 351 for(int i=0;i<len;i++){ 352 Node curroot=queue.poll(); 353 if(curroot.data==Integer.MAX_VALUE){ 354 System.out.print(space); 355 }else{ 356 //加上颜色 357 if(curroot.color==true) 358 System.out.print(space+curroot.data+"红"); 359 else 360 System.out.print(space+curroot.data+"黑"); 361 } 362 if(curroot.lchild!=null){ 363 queue.add(curroot.lchild); 364 } 365 else 366 queue.add(new Node()); 367 length++; 368 if(curroot.rchild!=null){ 369 queue.add(curroot.rchild); 370 } 371 else 372 queue.add(new Node()); 373 length++; 374 } 375 System.out.println(); 376 System.out.println(); 377 len=length; 378 height++; 379 h--; 380 } 381 System.out.println(); 382 } 383 } 384 //中序遍历 385 public void inOrder(Node root){ 386 if(root==null) 387 return; 388 inOrder(root.lchild); 389 System.out.print(root.data+" "); 390 inOrder(root.rchild); 391 } 392 393 /** 394 * 平衡操作---复制,原理见上一篇 395 * return Node修改了,不return 396 * 上色要从原节点开始 397 */ 398 399 public void rightRotation(Node nodeA){ 400 if(nodeA==null) 401 return; 402 else{ 403 Node nodeB=nodeA.lchild; 404 nodeA.lchild=nodeB.rchild; 405 if(nodeB.rchild!=null) 406 nodeB.rchild.father=nodeA; 407 nodeB.rchild=nodeA; 408 nodeB.father=nodeA.father; 409 if(nodeA.father==null){//根节点涂黑 410 this.root=nodeB; 411 nodeB.color=false; 412 //System.out.println("root: "+nodeB.data); 413 } 414 else{ 415 if(nodeA.father.lchild==nodeA) 416 nodeA.father.lchild=nodeB; 417 else 418 nodeA.father.rchild=nodeB; 419 } 420 nodeA.father=nodeB; 421 //return nodeA; 422 //System.out.println("after rightrotation: "+nodeA.data); 423 } 424 } 425 426 public void leftRotation(Node nodeA){ 427 if(nodeA==null) 428 return ; 429 else{ 430 Node nodeB=nodeA.rchild; 431 nodeA.rchild=nodeB.lchild; 432 if(nodeB.lchild!=null) 433 nodeB.lchild.father=nodeA; 434 nodeB.lchild=nodeA; 435 nodeB.father=nodeA.father; 436 if(nodeA.father==null) 437 this.root=nodeB; 438 else{ 439 if(nodeA.father.lchild==nodeA) 440 nodeA.father.lchild=nodeB; 441 else 442 nodeA.father.rchild=nodeB; 443 } 444 nodeA.father=nodeB; 445 //return nodeA; 446 } 447 } 448 449 450 451 /**修改内容 452 *再平衡-上色 453 */ 454 //p空或p.color==false,为黑,p.color==true;为红 455 public boolean isRed(Node p){ 456 if(p!=null&&p.color==true) 457 return true; 458 return false; 459 } 460 /**插入后修改 461 * 父节点为黑-不需要修改 462 * 父节点为红,则其肯定有黑祖父节点(其父节点肯定不为根节点,因为根节点为黑) 463 * ①叔叔为红-爷爷肯定黑 464 * ②叔叔为黑,他是父节点的右儿子 465 * ③叔叔黑,他是父节点的左儿子 466 */ 467 468 public void fixAfterInseart(Node newNode){ 469 while (newNode.father!=null&&newNode.father.color==true){ 470 //System.out.println("in fixAfterInsert"); 471 //父节点为红,必有祖父节点 472 Node father =newNode.father; 473 Node grandpa=newNode.father.father; 474 Node uncle; 475 if(father==grandpa.lchild){ 476 uncle=grandpa.rchild; 477 //①叔叔为红 478 if(isRed(uncle)){ 479 //System.out.println("fixAfterInsert case1"); 480 uncle.color=false; 481 father.color=false; 482 grandpa.color=true; 483 newNode=grandpa; 484 continue; 485 } 486 //叔黑, 487 //②当前节点为右孩子 488 if(newNode==father.rchild){ 489 //System.out.println("fixAfterInsert case2"); 490 newNode=father; 491 leftRotation(newNode); 492 Node p=father; 493 father=newNode; 494 newNode=p; 495 //②执行完触发③ 496 } 497 //System.out.println("fixAfterInsert case3"); 498 //③当前节点为左孩子 499 father.color=false; 500 grandpa.color=true; 501 rightRotation(grandpa); 502 //System.out.println("afterfix case3 newNode: "+newNode.data); 503 504 } 505 else{ 506 uncle=grandpa.lchild; 507 if(isRed(uncle)==true){ 508 //System.out.println("fixAfterInsert case4"); 509 uncle.color=false; 510 father.color=false; 511 grandpa.color=true; 512 newNode=grandpa; 513 continue; 514 } 515 if(newNode==father.lchild){ 516 //System.out.println("fixAfterInsert case5"); 517 //newNode=father; 518 rightRotation(father); 519 Node p=father; 520 father=newNode; 521 newNode=p; 522 //执行完5,会触发6 523 } 524 //System.out.println("fixAfterInsert case6"); 525 father.color=false; 526 grandpa.color=true; 527 leftRotation(grandpa); 528 } 529 530 531 } 532 //根节点黑化 533 this.root.color=false; 534 //System.out.println("afterfixinseart newNode: "+newNode.data); 535 } 536 537 /**删除后修改 538 * //因为我自己实现二叉搜索树删除节点时,是用的下面规则,所以顺延过来 539 * 540 * ①删除节点无子节点,不需要修改 541 * 542 * ②有右子树-用右子树最小值X节点替换被删节点(保留删除节点的颜色和指针,只对值替换,其实只动了替换节点X那里,动了之后新顶替x.child上来一个或者为null为X,以此回溯,调色) 543 * ,只有替换节点X是黑色才需要调色: 544 * 因为从子树抽调一个红色节点,并不影响红黑树特性 545 * 调色节点:(X,X.father) 546 * ③只有左子树-用左子树最大值节点替换被删节点X(保留删除节点的颜色和指针,只讲值替换,其实只动了替换节点X那里,动了之后新顶替x.child上来一个或者为null为X,以此回溯,调色) 547 * ,,只有该节点X是黑色才需要调色: 548 * 因为从子树抽调一个红色节点,并不影响红黑树特性 549 * 需要调色:(X,X.father) 550 * 551 * 调色的4种情况 552 * ①兄弟节点红 553 * ②兄弟节点黑,兄弟的两个孩子也黑 554 * ③兄弟黑,兄左孩子红,右孩子黑 555 * ④兄弟黑,兄弟有孩子红,左孩子颜色任意 556 */ 557 public void fixAfterdelete(Node p,Node father){ 558 Node brother=null; 559 while((p!=this.root)){ 560 //System.out.println("顶替节点:p"+p.data); 561 System.out.println("顶替节点父节点:p"+father.data); 562 System.out.println(father.lchild==p); 563 System.out.println(father.rchild==p); 564 if(father.lchild==p){ 565 brother=father.rchild; 566 //System.out.println("brother: "+brother.data); 567 //①兄红 568 if(isRed(brother)){ 569 System.out.println("fixAfterdelete case1"); 570 brother.color=false; 571 father.color=true; 572 leftRotation(father); 573 brother=father.rchild; 574 } 575 //兄黑 576 //②兄子全黑 577 if((!isRed(brother.lchild))&&(!isRed(brother.rchild))){ 578 System.out.println("fixAfterdelete case2"); 579 brother.color=true; 580 p=father; 581 //父红,涂黑,不用回溯 582 if(father.color){ 583 father.color=false; 584 break; 585 } 586 father=father.father; 587 }//兄子不全黑, 588 else{ 589 //③兄左孩子红,有孩子黑-先右旋--进入④状态 590 if(!isRed(brother.rchild)){ 591 System.out.println("fixAfterdelete case3"); 592 brother.lchild.color=false; 593 brother.color=true; 594 rightRotation(brother); 595 brother=father.rchild; 596 } 597 //④兄右孩子红,左孩子颜色任意-左旋 598 System.out.println("fixAfterdelete case4"); 599 brother.color=father.color; 600 father.color=false; 601 brother.rchild.color=false; 602 leftRotation(father); 603 break; 604 } 605 } 606 else{ 607 brother=father.lchild; 608 //①兄红 609 if(isRed(brother)){ 610 System.out.println("fixAfterdelete case5"); 611 brother.color=false; 612 father.color=true; 613 rightRotation(father); 614 brother=father.lchild; 615 } 616 //兄黑 617 //②兄子全黑 618 if((!isRed(brother.lchild))&&(!isRed(brother.rchild))){ 619 System.out.println("fixAfterdelete case6"); 620 brother.color=true; 621 p=father; 622 //父红,涂黑,不用回溯 623 if(father.color){ 624 father.color=false; 625 break; 626 } 627 //father.color=false; 628 father=father.father; 629 //回溯 630 }//兄子不全黑, 631 else{ 632 //③兄右孩子红,左孩子黑-先右旋--进入④状态 633 if(isRed(brother.lchild)==false){ 634 System.out.println("fixAfterdelete case7"); 635 brother.lchild.color=false; 636 brother.color=true; 637 leftRotation(brother); 638 brother=father.rchild; 639 } 640 //④兄左孩子红,右孩子颜色任意-右旋 641 System.out.println("fixAfterdelete case8"); 642 brother.color=father.color; 643 father.color=false; 644 brother.lchild.color=false; 645 rightRotation(father); 646 break; 647 } 648 } 649 } 650 } 651 652 public static void main(String args[]) { 653 RedBlackTree t=new RedBlackTree(); 654 t.inseart(t.root,8); 655 t.inseart(t.root,5); 656 t.printTree(t.root); 657 t.inseart(t.root,1); 658 t.printTree(t.root); 659 t.inseart(t.root,11); 660 t.printTree(t.root); 661 t.inseart(t.root,9); 662 t.printTree(t.root); 663 t.inseart(t.root,13); 664 t.printTree(t.root); 665 t.inseart(t.root,7); 666 t.printTree(t.root); 667 t.inseart(t.root,6); 668 //t.printTree(t.root); 669 t.inseart(t.root,12); 670 //t.printTree(t.root); 671 t.inseart(t.root,16); 672 //t.printTree(t.root); 673 t.inseart(t.root,2); 674 //t.printTree(t.root); 675 t.inseart(t.root,3); 676 //t.printTree(t.root); 677 t.inseart(t.root,4); 678 //t.printTree(t.root); 679 680 t.printTree(t.root); 681 t.delete(t.root,11); 682 t.printTree(t.root); 683 684 t.deleteMin(t.root); 685 t.printTree(t.root); 686 t.deleteMin(t.root); 687 t.printTree(t.root); 688 t.deleteMin(t.root); 689 t.printTree(t.root); 690 t.deleteMin(t.root); 691 t.printTree(t.root); 692 t.deleteMin(t.root); 693 t.printTree(t.root); 694 695 696 // t.deleteMax(t.root); 697 // t.printTree(t.root); 698 // t.deleteMax(t.root); 699 // t.printTree(t.root); 700 // t.deleteMax(t.root); 701 // t.printTree(t.root); 702 // t.deleteMax(t.root); 703 // t.printTree(t.root); 704 705 t.inOrder(t.root); 706 } 707 708 }
结语:画图不易,233,可能有很多错误的小细节,欢迎指正。
参考:
https://www.cnblogs.com/lycroseup/p/7324229.html
https://blog.csdn.net/u012149181/article/details/88789595
这个总结的最好:
https://www.jianshu.com/p/96e652ccf720
https://www.jianshu.com/p/84416644c080
