机器学习--逻辑回归

　　逻辑回归主要用于二分类问题中，对于一个样本数据集：{（x1,y1）,(x2,y2),.....(xn,yn)},x表示样本特征，y表示样本类别（通常取值为0,1）。逻辑回归的目标是对算法训练完成之后，输入一个待分类样本，输出该样本的类别（0或者1）。因此引入数学上的sigmoid函数，该函数的形状为为's'型，在x正半轴x越大，函数值越接近1，在x轴负半轴，x越小，函数值越接近0.当x等于0时，函数输出等于0.5.sigmoid函数的这一性质刚好可以用来对数据进行分类，如果输出值为>0.5,则认为该数据样本归入‘1’类;如果输出值<0.5,则将该样本归入‘0’类。函数的表达式如下：

　　                                              

该函数的图像如下：

　　　　　　　　　　　　　　　　　　　　

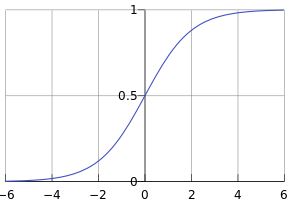
从图中可以看出，函数定义域为实数，值域在（0,1）之间。

假设样本数据中x具有N个特征，则 z = w0*x0+w1*x1+w2*x2+......+wn*xn.

将每个待测样本的x值带入上式，就可以求出该样本的对应的值，比较该值和0.5的大小，就可以确定该样本的类别。

那么问题就转化为，知道一批样本数据，求w0.......wn的参数。这也是机器学习训练的分类器的工作量最大的地方。求参数的过程具体可以使用梯度上升法。主要思想是利用迭代的方式求得回归参数。

求得回归参数后，就可以认为分类器训练完成，接着对训练器进行测试。在《机器学习实战》这本书中，作者详细的介绍了分类器的训练过程和测试过程，但是对相关的理论推导一笔带过，本文不再做详细介绍，后面专门写一篇数学推导的过程。

《机器学习实战》中的代码如下：

# -*- coding: utf-8 -*-
"""
Created on Sat Aug  6 10:23:59 2016

@author: admin
"""
from numpy import *
def loadDataSet():
    dataMat = [];labelMat = []
    fr = open('testSet.txt')
    for line in fr.readlines():
        lineArr = line.strip().split()
        dataMat.append([1.0,float(lineArr[0]),float(lineArr[1])])
        labelMat.append(int(lineArr[2]))
    return dataMat,labelMat
    
def sigmoid(inX):
    return 1.0/(1+exp(-inX))
    
def gradAscent(dataMatIn,classLabels):
    dataMatrix = mat(dataMatIn)
    labelMat = mat(classLabels).transpose()
    m,n = shape(dataMatrix)
    alpha = 0.001
    maxCycles = 500
    weights = ones((n,1))
    for k in range(maxCycles):
        h = sigmoid(dataMatrix*weights)
        error = (labelMat - h)
        weights = weights + alpha * dataMatrix.transpose()*error
    return weights
    
def plotBestFit(wei):
    import matplotlib.pyplot as plt
    weights = wei.getA()
    dataMat,labelMat = loadDataSet()
    dataArr = array(dataMat)
    n = shape(dataArr)[0]
    xcord1 = [];ycord1 = []
    xcord2 = [];ycord2 = []
    for i in range(n):
        if int(labelMat[i]) == 1:
            xcord1.append(dataArr[i,1]);ycord1.append(dataArr[i,2])
        else:
            xcord2.append(dataArr[i,1]);ycord2.append(dataArr[i,2])
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord1,ycord1, s=30, c = 'red',marker = 's')
    ax.scatter(xcord2,ycord2, s=30, c = 'green')
    x = arange(-3.0, 3.0, 0.1)
    y = (-weights[0] - weights[1]*x)/weights[2]
    ax.plot(x,y)
    plt.xlabel('X1');plt.ylabel('X2')
    plt.show()
    
def stocGradAscent0(dataMatrix,classLabels):
    m,n = shape(dataMatrix)
    alpha = 0.01
    weights = ones(n)
    for i in range(m):
        h = sigmoid(sum(dataMatrix[i]*weights))
        error = classLabels[i] - h
        weights = weights + alpha * error * dataMatrix[i]
    return weights
    
def stocGradAscent1(dataMatrix,classLabels,numIter=150):
    m,n = shape(dataMatrix)
    weights = ones(n)
    for j in range(numIter): 
        dataIndex = list(range(m))
        for i in range(m):
            alpha = 4/(1.0+j+i) + 0.1
            randIndex = int(random.uniform(0,len(dataIndex)))
            h = sigmoid(sum(dataMatrix[randIndex]*weights))
            error = classLabels[randIndex] - h
            weights = weights + alpha * error * dataMatrix[randIndex]
            del(dataIndex[randIndex])
    return weights
    
def classifyVector(inX,weights):
    prob = sigmoid(sum(inX*weights))
    if prob > 0.5 : 
        return 1.0
    else:
        return 0.0
        
def colicTest():
    frTrain = open('horseColicTraining.txt')
    frTest = open('horseColicTest.txt')
    trainingSet = []
    trainingLabels = []
    for line in frTrain.readlines():
        currLine = line.strip().split('	')
        lineArr = []
        for i in range(21):
            lineArr.append(float(currLine[i]))
        trainingSet.append(lineArr)
        trainingLabels.append(float(currLine[21]))
    trainWeights = stocGradAscent1(array(trainingSet),trainingLabels,500)
    errorcount = 0;numTestVec = 0.0
    for line in frTest.readlines():
        numTestVec += 1.0
        currLine = line.strip().split('	')
        lineArr = []
        for i in range(21):
            lineArr.append(float(currLine[i]))
        if int(classifyVector(array(lineArr),trainWeights)) != int(currLine[21]):
            errorcount += 1
    errorRate = (float(errorcount)/numTestVec)
    print('the error rate of the average error is :%f' %errorRate)
    return errorRate
    
def multiTest():
    numTests = 10;errorSum = 0.0
    for k in range(numTests):
        errorSum += colicTest()
    print('after %d iterations the average error rate is:%f'%(numTests,errorSum/float(numTests)))

使用书中的样本数据对算法进行训练，可以得到和书中相似的结果。