《排序算法系列6》归并排序

1 思想

归并排序（MERGE-SORT）是利用归并的思想实现的排序方法，该算法采用经典的分治（divide-and-conquer）策略（分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起，即分而治之)。

2 举例

可以看到这种结构很像一棵完全二叉树，本文的归并排序我们采用递归去实现（也可采用迭代的方式去实现）。分阶段可以理解为就是递归拆分子序列的过程，递归深度为log₂n。

合并相邻有序子序列

再来看看治阶段，我们需要将两个已经有序的子序列合并成一个有序序列，比如上图中的最后一次合并，要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列，合并为最终序列[1,2,3,4,5,6,7,8]，来看下实现步骤。

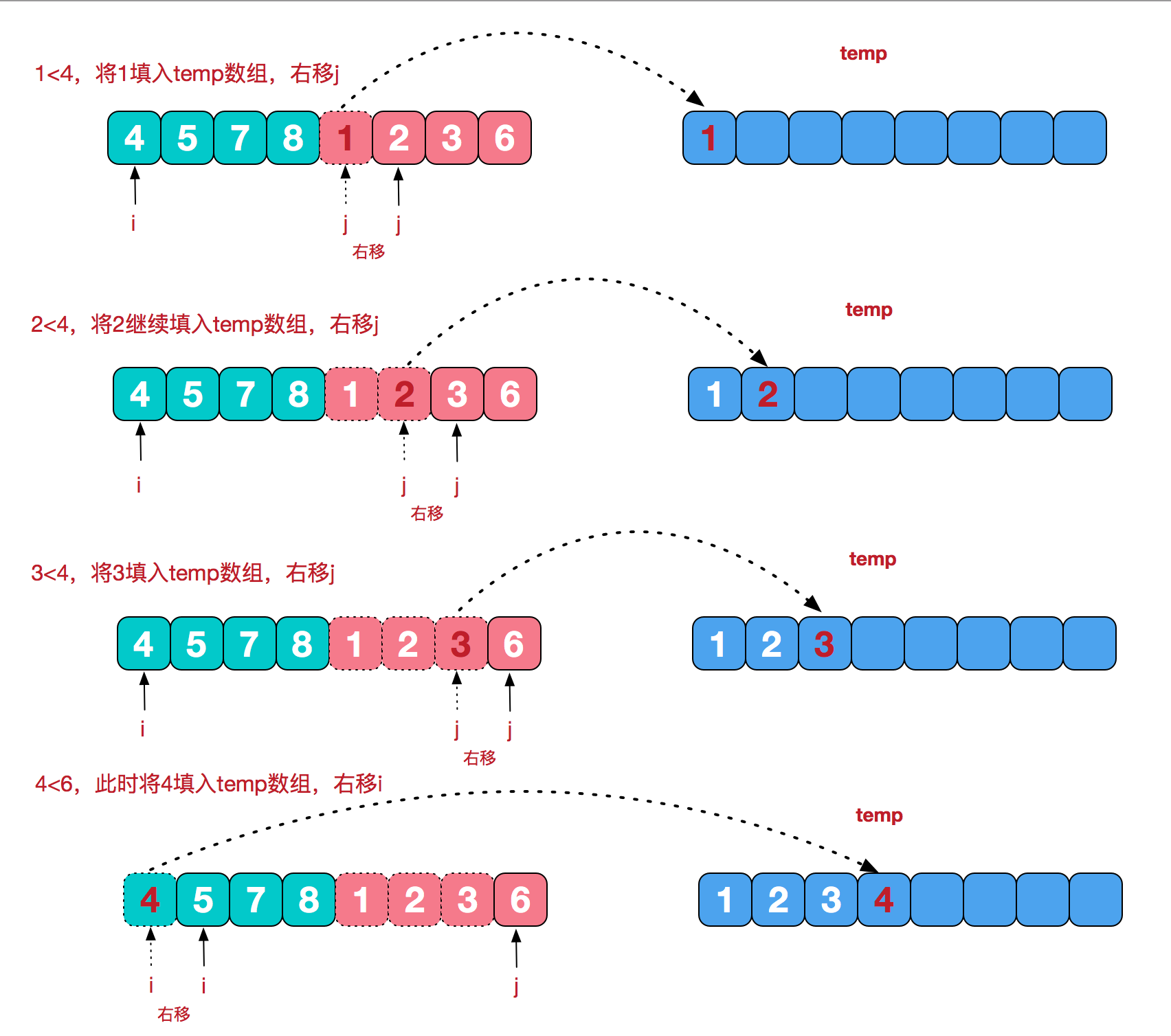
归并排序动态演示

 

3 代码实现

    public static void main(String[] args) {
        int[] arr = { 8, 4, 5, 7, 1, 3, 6, 2 };
        int[] temp = new int[arr.length];// 归并排序需要一个额外的空间
        mergeSort(arr, 0, arr.length - 1, temp);
        System.out.println("归并排序后的结果" + Arrays.toString(arr));
    }
    
    /**
       *  通过递归实现数组的分阶段  然后调用数组合并方法
      * 从而实现归并排序的分而治之思想
     * @param arr   需要排序的数组
     * @param left  排序数组的开始索引
     * @param right 排序数组的结束索引
     * @param temp  辅助数组,用于接受排序的结果
     * void
     */
    public static void mergeSort(int[] arr, int left, int right, int[] temp) {
        if (left < right) {
            int mid = (left + right) / 2;// 中间索引
            // 向左递归进行分解
            mergeSort(arr, left, mid, temp);
            // 向右递归进行分解
            mergeSort(arr, mid + 1, right, temp);
            // 合并
            merge(arr, left, mid, right, temp);
        }
    }

    /**
     *  治阶段： 将分开的2个数组合并s 
     * 
     * @param arr   排序的原始数组
     * @param left  左边有序数组
     * @param mid   中间索引
     * @param right 右边索引
     * @param temp  中转的数组
     */
    public static void merge(int[] arr, int left, int mid, int right, int[] temp) {
        int i = left;// 左边有序序列的初始索引
        int j = mid + 1;// 右边有序序列的初始索引
        int t = 0; // 指向temp数组的当前索引

        // 步骤一:
        // 先把左右两边的数据按照规则填充到temp数组
        // 直接左右两边的数组 有一边处理完毕为止
        while (i <= mid && j <= right) {
            // 如果左边的有序序列的当前元素 小于等于右边有序序列的当前元素
            // 把左边的元素添加到temp数组
            if (arr[i] <= arr[j]) {
                temp[t] = arr[i];
                i++;
                t++;
            } else {
                temp[t] = arr[j];
                j++;
                t++;
            }
        }

        // 步骤二:
        // 把有剩余的数组一边的数据依次填充到temp
        while (i <= mid) {
            temp[t] = arr[i];
            t++;
            i++;
        }
        while (j <= right) {
            temp[t] = arr[j];
            t++;
            j++;
        }

        // 步骤三:
        // 把temp拷贝到arr
        //初始化t 
        t = 0;
        int tempLeft = left;
        // 注意 并不是每次都拷贝所有 因为不需要拷贝temp 只需要拷贝当前的排好序的数组
        while (tempLeft <= right) {
            arr[tempLeft] = temp[t];
            t++;
            tempLeft++;
        }
    }

4 时间复杂度

假如n个元素使用归并排序的时间复杂度为T(n),那么由于归并排序使用的是分治思想，T(n)=2*T(n/2)+n,其中n就是两个子区间合并的时间复杂度，这个从合并函数可以看出来。可以推导出以下公式：

                        T(1) = C；   n=1 时，只需要常量级的执行时间，所以表示为 C。
                         T(n) = 2*T(n/2) + n； n>1

经过进一步推导，可以得到T(n)=2^k * T(n/2^k) + k * n,我们假设T(1)=T(n/2^k),也就是说当n/2^k个元素的进行归并排序，达到递归终止条件时，n/2^k=1,得到：k=logn

于是：

                                             T(n)=Cn+nlog2n

归并排序的时间复杂度就是O(nlogn),跟数组的有序度其实并没有什么关系，是非常稳定的时间复杂度。

 5 时间复杂度速度测试

　　// 归并排序
    public static void main(String[] args) {
        speedTest(8000000);
    }

    /**
       * 创建一个随机数组 然后调用排序方法 得到时间
     * 
     * @param number 创建的随机数组个数
     */
    public static void speedTest(int number) {
        int[] arr = new int[number];
        int[] arr2 = new int[number];
        for (int i = 0; i < arr.length; i++) {
            arr[i] = (int) (Math.random() * 800000);
        }

        SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
        Date date1 = new Date();
        String time1 = simpleDateFormat.format(date1);
        System.out.println("排序前的时间为:" + time1);

        // 调用上面的归并排序方法
        mergeSort(arr, 0, arr.length-1, arr2);

        Date date2 = new Date();
        String time2 = simpleDateFormat.format(date2);
        System.out.println("排序后的时间为:" + time2);
    }

归并排序速度测试结果

8万个数据测试结果大约需要不到1秒

 80万个数据测试结果大约需要不到

 800万个数据测试结果大约需要2秒

8000万个数据测试结果大约16秒