今天是2020年2月7日星期五。分享一个箴言：世界上只有一种英雄主义，那就是认识生活的真相后依然爱它。
好了，开始今天的内容，决策树算法。书中针对该算法，洋洋洒洒讲了很多内容，对初学者不太友好，我初读本章内容时，头大的很。但等到学完，头脑里有了框架之后，该算法的学习就清楚了很多，所以稍后会写一下该算法的脉络主线，带着框架去完成该算法的搭建，这样学习要轻松点。另外，在记录这个学习过程前，我一般会在网上多看几篇相关内容，发现各个内容各有所长，相应的，大家也要各取所需。
脉络主线：(1)总起讲基本决策树模型，阐述决策树基本思路；(2)以ID3、C4.5为例分讲三步骤：特征选择、决策树生成、决策树剪枝；(3)最后以经典CART算法结束决策树的学习，该算法应用决策树基本思路，细品起来还是挺不一样的。
GitHub：https://github.com/wangzycloud/statistical-learning-method
决策树算法
引入
决策树算法是一种呈树形结构的基本分类与回归方法，本内容主要讨论用于分类的决策树，基于特征对实例进行分类。像书中提到的，决策树算法可以认为是if-then规则的集合，即根据特征的不同取值进行分支选择；也可以认为是定义在特征空间与类空间上的条件概率分布，即通过构建决策树将特征空间划分成不同子空间，叶节点上的子空间对应条件概率最大的类，分类时将‘特征符合’的实例点强行分到该空间对应的类上（认为顺着根节点到叶节点，在符合各内部节点特征的条件下，实例点是该类的条件概率最大）。
学习时，该算法利用训练数据集，根据损失函数最小化的原则建立决策树模型；预测时，对新的数据，利用决策树模型进行分类。决策树的学习，通常由三个步骤构成：特征选择、决策树的生成、决策树剪枝。接下来按照提到的脉络主线，记录决策树模型基本思路、三大步骤(ID3、C4.5)、CART算法。
决策树模型
先来看一下定义：
用圆框表示内部节点，用方框表示叶节点，有了树形结构，它是怎么分类的呢？这里我们用判断来诊人员是否需要输液的例子：
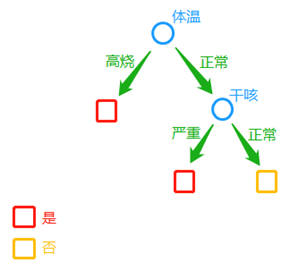内部节点表示特征，用决策树进行分类，就是从根节点开始，对实例的某一特征进行测试。根据测试结果，选择合适的分支，将实例分配到该分支对应的子节点上，这时每一个子节点对应着该特征的一个取值。递归的对实例进行测试，直至到达叶节点，最后将实例分配到叶节点对应的类中。看一下图中的例子，对于新的来诊人员，从我们的生活经验上，医生一般会让我们先测试一下体温，如果体温过高的话，基本上是需要打个退烧针了；测完体温后，医生会进行听诊，然后看咽喉是否发炎，了解下咳嗽情况。也就是说，判断完体温特征后，再判断下一个特征干咳是否严重，每个特征判断完毕，就可以根据不同的分支结果，确定患者是否需要输液了。
对决策树的理解，书中有两个解释。
首先第一个，决策树与if-then规则，也就是与选择分支结构的关系。从判断来诊人员是否需要输液的例子上，我们可以看到决策树模型分类的过程，就是从根节点到叶节点的一条路径。路径上内部节点的特征对应着选择分支的判别条件，子节点对应着条件的不同分支，叶节点的类对应着判别的结果。另外，构成分类决策的所有路径，也就是选择分支的所有条件，具有一个重要的性质：互斥且完备。每个实例从根节点判别开始，到叶节点得到分类结果结束，都有属于自己的一条路径，有且仅有一条路径，并且该决策树能把训练集所有实例判别。
第二个是从条件概率分布的角度，也就是在给定特征条件下类的条件概率来理解决策树算法。书中指出，这一条件概率分布定义在特征空间的一个划分上。在我的理解中，这句话要拆开来看，(1)求谁的概率，在哪个条件上？(2)特征空间是怎样划分的？
第一点很明确，求叶节点类别的概率，条件是各项已知的特征。在输液例子中，要求的类别：是否需要输液；特征有两个：体温情况、干咳程度。要求叶节点的条件概率就是求分别在给定体温高烧、体温正常干咳严重、体温正常干咳正常条件下，是否需要输液的概率。对于第二点，说起特征空间的划分，很容易想到我们之前接触到的kd树算法，它就是对特征空间进行划分，轮流从不同维度取中位数对特征空间进行划分。在决策树算法中，输液的这个例子，如果将各个特征，看成不同维度（几个特征，几个维度坐标轴），进行特征选择的过程，不就是将特征空间逐步划分成小单元的过程。简单讲，将特征数目看成维度数目，将特征值取值的数目看成该维度坐标轴的切分点。从根节点到叶节点的路径，不就是在特征空间中从原点行走到某个小空间单元的过程（决策树中的一条路径对应于划分的一个单元）。
再返回去看第一点在给定特征下的条件概率，也就是根据在不同特征上的取值，将特征空间划分成了小单元。该条件概率就是在各个叶子节点小单元的条件下（条件也就是决策树中从根节点到叶子节点，每层特征取固定的值），将每个单元定义成某个类别的概率。另外，各叶子节点（单元）上的条件概率往往偏向于一个类，即属于某一类的概率较大。比如说，体温高烧这条路径对应的叶子节点，需要输液的条件概率要远远大于体温高烧不需要输液的条件概率；‘体温正常干咳正常’这路径对应的叶子节点，不需要输液的条件概率远远大于‘体温正常干咳正常’需要输液的概率。
决策树学习
从上一部分的分析中，可以看出，决策树学习本质上就是从训练数据集中，通过特征选择归纳出一组分类规则。另外，树形结构每层选择‘作为根节点的特征’不同，构造出来的决策树也就不同。同时能对训练集进行正确分类的决策树可能有多个，也可能一个没有。我们的目标是通过损失函数，学习到一个对训练数据集更好分类前提下，能够对新数据有很好泛化能力的决策树模型。
这里提到了一个最优特征的概念，表示特征之间的重要性是不一样的，构建决策需要从最重要的特征开始考虑，下一层选择次优的特征，下下次选择次次优的特征。这是有实际意义的，以是否输液为例，对于医生来讲，判断一个感冒病人是否需要输液，“体温是不是高”这个特征表现，要远比“干咳严不严重”的特征表现，更能决定是不是需要输液。一旦体温很高，这直接决定了需要输液，“判断”这个过程的不确定性，直接降了下来（体温高烧->需要输液）；而如果先判断“干咳严不严重”，这个特征表现不能全然断定需要输液。还要继续用“体温高不高”这个特征再测试一下才能确定。这个“判断”过程的不确定性，是逐步降下来（干咳正常->体温高烧->需要输液）。
通过上述方法构建的决策树，可能对训练数据集有很好的分类能力，但是对未知的测试数据却未必有很好的分类能力，有可能发生过拟合现象。直观点来说，决策树构建的越细密，训练集特征空间切分也就越微小越明确，有可能邻近个几个小空间都属于一类。完全没必要切分这么细，树形越复杂越容易出现过拟合。这就需要我们对已生成的树进行自下而上的剪枝，将树变的更简单，从而具有更好的泛化能力。具体来讲就是去掉过细的叶节点，使其退回到父节点，让父节点成为新的叶子节点。当然，如果特征的数量较多，在构建决策树的开始，就可以对特征进行选择，只留下对数据集有很好分类能力的特征。
通过上述决策树学习算法的描述，可以发现生成决策树的过程，是一个细分特征空间，对实例点进行局部选择的过程。尽可能让每个实例从原点到达特征空间的某一个具有确定类别的区域，且该区域能够对实例做出正确的判断；如果树形过大过细过复杂，就意味着决策树能够对当前训练数据集有非常非常好的判断（都是长路径）。一旦来新数据（需要新路径进行分类），找不到分类规则就不能判断，因此需要将树形消减，去掉过细的叶节点，让最优的特征发挥作用。从主要特征上对新数据判断（短的路径），将树形修减到合适的程度也就是考虑全局最优。
特征选择
在决策树学习的过程描述里，提到了一个“最优特征”的概念，也就是实例点在特征选择分支的条件判断中，从根节点到叶节点，“特征判断”有一个先后顺序，看一下判断患者是否需要输液的例子，先判断体温？还是先判断干咳？一般经验下，肯定是先判断是不是出现高烧，也就是判断体温这个特征比判断干咳的特征优先级高。
特征选择就是决定用哪个特征来划分特征空间，关键在于选取对训练数据具有分类能力的特征，这样可以提高决策树学习的效率。如果利用一个特征进行分类的结果与随机分类的结果没有很大差别，则称这个特征是没有分类能力的。经验上丢掉这样的特征对决策树学习的精度影响不大，通常特征进行选择的准则是信息增益或信息增益比。这里我们使用书上的例5.1。
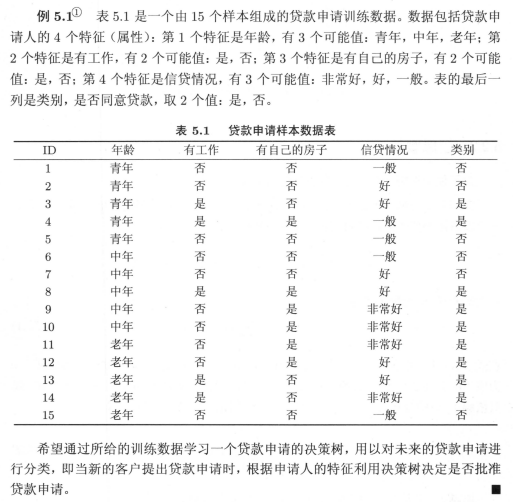
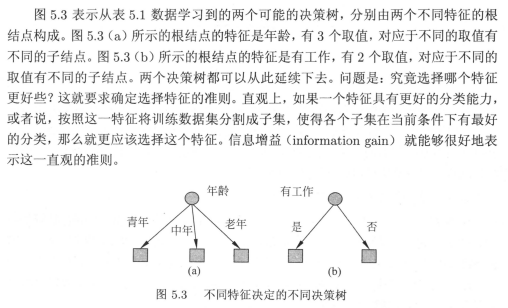
通过该图解，可以看到选择不同的特征作为根节点，可以得到不同的决策树；某特征的不同取值，成为子节点的不同分支。
至于信息增益这个概念，我在刚开始接触这本书的时候，理解起来困难还是蛮大的，概率没怎么学，熵、条件熵也不知道是啥。看到“熵”这个字，脑子里全是高中物理里的“熵”，也就是体系混乱程度的度量，本书里边用“熵”表示随机变量不确定性的度量，这两个定义好像表达的是一个意思。掷出硬币后，在空中翻转是一个旋转不定的过程（动能势能不断的转换），这中间正面朝上是个说不准的事情，不确定性非常高，一会正一会反；硬币正面朝上落在桌子上了，静止不动（相对平衡的体系状态），正面朝上就是一个确定的事情。然后先看“信息增益”的作用是什么，再去理解“信息增益”是个啥。
在我的理解里，“信息增益”是让“熵”减小的能力度量单位。也就是某个东西能让目标整体的不确定性减小，就是指通过特征A的划分让分类目标的不确定性减小的能力度量单位。比如说，判断体温高烧要比判断是否干咳更能决定是否需要输液，即体温特征比干咳特征在是否输液这个分类目标上，具有更好的让不确定性减少的能力。简而言之，信息增益就是得知特征X而使得类Y的信息不确定性减少的程度。
先来看一下熵与条件熵的定义。
之前提到，高中物理里边的熵是体系的混乱程度，反映到信息论与概率统计中，不正好就是随机变量取值的不确定性。由公式5.1，可以看到离散随机变量X的熵与该随机变量具体取什么值没有关系，只与它取值的概率分布有关。看一下掷硬币这种二分类的例子。
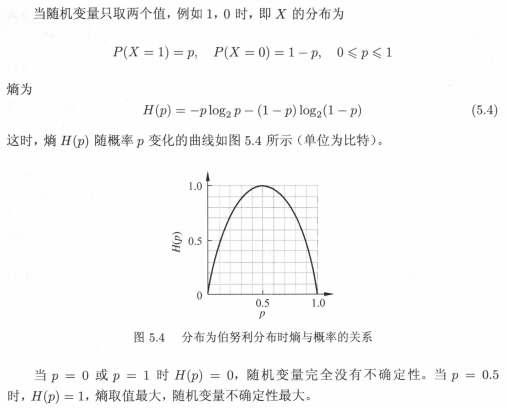
类似于掷硬币的过程，只有正反面两种结果，P(正面)≈P(反面)，如图5.4所示，p=0.5时，掷硬币的结果最不确定（这个时候的熵最大），是正是反都有可能，但是哪一面最有可能呢？谁也说不上，因为正反面的概率一分为二，都是50%的概率。如果改变一下硬币的形状，变成类似圆台的形状，让面积大的一侧是反面，面积小的一侧是正面（同时把高拉长）。这时再掷硬币，谁都知道面积大的面会朝下（90%），这是很确定的事情，反面朝上的概率很小（10%），这个时候再去猜测哪个面会朝上，大家肯定都会说是正面，因为正反面的概率差别很大，这件事情的确定性大（这个时候熵比较小）。
顾名思义，条件熵反映的是随机变量Y在给定随机变量X条件下的不确定性。这里公式5.5有待证明，但在公式的直观表示上（公式右端，每个条件下Y的熵乘以条件出现的概率再加和），可以看出H(Y|X)的求法。Y在Xi的条件下，要把所有Xi、Y联合出现的概率求出条件熵（Y|Xi熵），乘以该Xi条件下Y|Xi熵的概率，最后加和。
当熵和条件熵中的概率由训练数据集通过极大似然估计得到时，对应的熵和条件熵分别称为经验熵、经验条件熵。如果有0概率，令0log0=0。
熵是不确定性的衡量，信息增益是让不确定性减少的程度，在决策树中，也就是得知特征X的信息从而使得类Y的信息的不确定性减少的程度，具体定义如下。
这里假设存在训练数据集D，D中数据共有K个类别Ck，k=1,2,3,…,K，其中：
|D|表示样本容量，即样本个数；
|Ck|表示属于Ck这个类别的样本个数；
设特征A有n个不同的取值{a1,a2,…,an}，根据A的取值将数据集D划分成n个子集D1,D2…Dn，其中：
|Di|表示子集Di样本容量，即子集Di的样本个数；
根据假设，有以下等式成立：
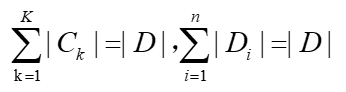
记子集Di中属于类Ck的样本的集合为Dik，即Dik=Di∩Ck，其中：
|Dik|表示Dik样本容量，即集合Dik的样本个数；
汇总如下：
于是得到信息增益算法5.1如下：
例5.2是根据表5.1贷款申请样本数据表计算最优特征的过程。注意到，根据算法5.1，首先计算整个集合D对于分类问题的检验熵，也就是得到当前数据判断类别的不确定性。其次，逐个计算每个特征条件下，对数据集D的检验条件熵。最后分别计算各个特征的信息增益，并进行比较，选择信息增益最大的特征作为最优特征。
在算法5.1部分，各个熵的计算直接给出了计算公式，从公式的直观形式上，通过各事件出现的频率来估计概率，好像是极大似然估计得到的公式，但是书中并没有提及公式来源。
要知道，信息增益是ID3算法中进行最优特征选择的准则，在接下来的决策树生成部分，会详细写一下ID3算法。与ID3算法同时学习的是C4.5算法，自然而然，C4.5算法是ID3算法的改进，改进的地方很简单，就是将特征选择的准则由信息增益改为了信息增益比。先来看一下信息增益比的计算方式，再分析优点。
从公式5.10中可以看到，信息增益比多了一个分母。分母是数据集D关于每个特征取值的熵。也就是对某个特征计算完信息增益后，要比上数据集D关于该特征取值划分成对应子类的熵。
C4.5作为ID3算法的改进，要想了解信息增益比的优点，可以先了解信息增益的缺点。用信息增益作为划分训练数据集的特征，存在偏向于选择取值较多的特征的问题。这一点怎么理解呢？在公式5.8中可以发现，如果某个特征取值较多，该取值的实例数目所占的比例大，导致该特征的条件经验熵高，因此该特征的信息增益值大。其实就是相当于，取该值的特征非常多，该特征成为了去往叶节点的必经路径，形成了往这里划分一定能行这种逻辑，划分后必然降低不确定性，但是该特征不一定具有很好的特征选择能力。
使用信息增益比就可以对这个问题进行改进，注意到公式5.10中HA(D)的描述，针对特征A的取值计算数据集D的熵，这个熵与H(D)的区别在于子集划分规则不同。H(D)是关于类别Y的熵，HA(D)是关于特征A子集的熵。这里有待深入学习，没有解释为什么可以校正。
决策树的生成
本节内容从ID3算法入手，学习一下决策树的生成，上文提到ID3算法的核心是在决策树各个节点上应用信息增益准则选择特征，递归的构建决策树。具体方法是：从根节点开始，对节点计算所有可能的特征的信息增益，选择信息增益最大的特征作为节点的特征，由该特征的不同取值建立子节点；再对子节点递归的调用以上方法，构建决策树；直到所有特征的信息增益均很小或者没有特征可以选择为止。
要知道ID3算法只有树的生成，没有剪枝过程，因此生成的决策树容易发生过拟合。算法如下：ID3 相当于用极大似然法进行概率模型的选择，怎么理解？(不理解...@_@)
算法流程图：
具体示例：
C4.5的生成算法与ID3算法相似，特征选择改进为信息增益比。
决策树剪枝
前文提到，如果构建的决策树非常细密，树形非常复杂，会容易发生过拟合现象。这样的树往往对训练数据的分类很准确，但对未知的测试数据进行分类的时候，却没有那么准确。原因在于学习时过多的考虑如何提高对训练数据的正确分类，从而构建出了复杂的决策树。因此，是否可以考虑决策树的复杂度，对已生成的决策树进行简化。
简化的过程称为剪枝，从已生成的决策树上剪掉一些子树或者叶节点，并将其根节点或父节点作为新的叶节点，从而简化决策树模型。书中提到，决策树的剪枝往往通过极小化决策树整体的损失函数来实现。书中只是描述了公式及算法，并没有阐述为什么这样做可以，这里提出一个不成熟的观点和理解。
首先明确熵是不确定性的度量。构建决策树的过程，是将整个特征空间划分为不同的小区域，通过一系列的特征判断，训练集中的各个数据有了明确的安放位置，特征空间内井井有条。生成决策树，就是能够最快的将不同数据划分到相应叶节点的子空间中，且该子空间内的数据尽可能属于同一类。决策的过程，就是在给定某个特征的条件下，数据集D分类的不确定性减少；那么对应到叶节点，给定叶节点特征路径的条件下，数据集D分类的熵应尽可能小。也就是说叶节点对应的数据，应该尽可能的一致，大家都属于一个类最好了（算法5.2如果信息增益小于阈值，将实例数最大的类作为节点类标记，也就是叶节点对应的数据不一定属于同一个类）。
现在考虑这棵决策树在训练集上构建的好不好，是不是就可以通过叶节点的不确定性程度来反映。如果每个叶节点都是一类，也就是在叶节点特征路径的条件下，数据集D内的数据确定是属于某个类，不确定性为零，就说这棵决策树构建的非常好，但相应的，树形会非常复杂。如果每个叶节点中数据不属于同一个类，也就是在叶节点特征路径的条件下，数据集D内的数据不能完全确定属于这个类，不确定性大，就不能说这是一棵好的决策树，相应的树形会比较简洁。可以发现，叶节点的熵和树形的复杂程度成反比关系，是不是可以利用该关系，设计一个损失函数，让决策树的分类能力和树形的复杂程度做一个平衡。看一下书中的计算公式以及剪枝算法。
设树T的叶节点个数为|T|，t是树T的叶节点，该叶节点上有Nt个样本点，其中k类的样本点数为Ntk个，k=1,2…K，Ht(T)为叶节点t上的经验熵，α≥0为参数，则决策树学习的损失函数可以定义为：
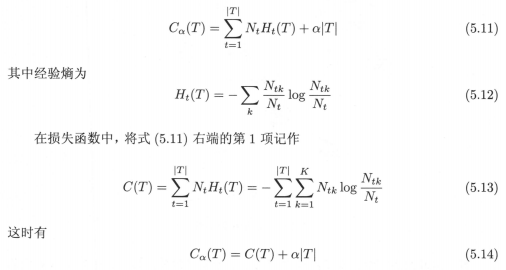
公式5.11右端第一项，每个叶节点的经验熵多乘了一个系数（该节点的样本个数），暂时看不出意义在哪里。在公式5.13上，该系数消去了一个分母，看不出别的门道来，貌似也没有把计算变简单，毕竟log后仍然求分数（小数过小是不是会导致溢出？log里的小数没有溢出问题，不知道是不是这个原因）。
在公式5.14中，可以看到C(T)表示模型对训练数据的预测误差，即模型与训练数据的拟合程度，也就是观点里边该决策树是否将数据集很好分类的能力。|T|表示模型复杂度，α控制两者之间的影响，相当于权重因子（数值大，则该项被优化的力度大）。较大的α促使选择较简单的决策树，较小的α促使选择较复杂的决策树，α=0意味着只考虑模型与训练数据的拟合程度，不考虑模型的复杂度（正则化项）。
可以看出，决策树生成只考虑了通过提高信息增益或者信息增益比对训练数据进行更好的拟合，而决策树剪枝通过优化损失函数还考虑了减小模型复杂度。图5.6是决策树剪枝过程的示意图，看一下剪枝算法：
CART算法
CART算法是分类与回归树(classification and regression tree)的简称，同样由特征选择、树的生成和剪枝组成，既可以用于分类也可以用于回归。与ID3、C4.5算法构建决策树不同的是，CART假设决策树是二叉树，内部节点特征取值为“是”和“否”，左分支是取值为“是”的分支，右分支是取值为“否”的分支，这样的决策树等价于递归的二分每个特征，将输入空间即特征空间划分成有限个单元。该算法同样是给定输入变量X条件下输出随机变量Y的条件概率分布的学习方法，在划分后的每个单元上确定预测的概率分布，也就是在输入给定的条件下输出的条件概率分布。
这里需要注意理解“递归的二分每个特征”，ID3算法构建决策树时，我们没有强调是一棵二叉树。因为每个特征的取值，不固定只有两个取值，我们根据该特征的取值，划分为不同子树，几个取值几个子树。现在“递归的二分每个特征”要构建一棵二叉树，是不是和多个取值的特征发生矛盾呢？没矛盾的话怎么处理呢？比如体温有三个取值：高温、正常、低温，递归的二分每个特征是指细分每个特征的取值。之前体温特征内部节点的判别结果有三个分支，现在内部节点判别条件变为是否高温、是否正常、是否低温，相应内部节点的判别结果分成两个分支。具体做法仍然是生成和剪枝两个部分。
CART-分类树的生成
类似于ID算法的生成过程，CART分类树使用基尼指数来选择最优特征，同时决定该特征的最优二值切分点。先看一下基尼指数的定义：
可以看到公式5.23计算方式是公式5.22在二分类问题下的特殊情况，公式5.24使用频率估计概率，得到样本集合D下判别K类的基尼指数。类似于条件熵，在已知某特征取值下的表示为：
基尼指数Gini(D)表示集合D的不确定性，基尼指数Gini(D,A)表示经A=a分割后集合的不确定性。与熵类似，基尼指数的值越大，样本集合的不确定性也就越大。CART生成算法：
算法流程图：
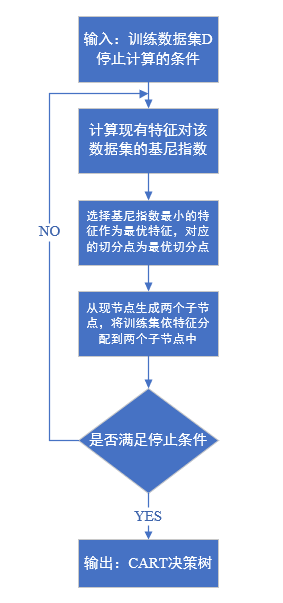
计算例子：
CART-回归树的生成
顾名思义，回归树是决策树算法在回归问题上的应用。
我们先来思考一下，回归问题应该和分类问题有什么差异，再看接下来的内容。
第一个问题，回归树模型是什么样子的。之前提到的决策树模型，都是关于分类问题，通过特征选择对特征空间进行划分，被划分到决策树叶子节点对应子空间上的实例，属于同一类别；我们知道回归问题输出变量应为连续值，是不是就意味着回归问题里，类别数目非常非常多，多到像连续值的排列一样。子空间划分成的各个小单元，标记不再是类别，而是一系列数值。
第二个问题，对什么进行选择，从而划分特征空间。分类树中，各个数据基本上都是非数值型的，存在很多特征分量，我们根据各个特征的取值概率，找最优的特征作为切分数据集的标准；在回归问题中，输入一般为数值型数据，决策树模型需要找到切分点，回归问题中怎么处理呢？
第三个问题，切分点选择的准则是什么。分类树中，我们通过信息增益或者信息增益比来选择最优特征作为子树节点的切分点；在回归树中，要通过什么准则对什么进行选择，从而划分特征空间？
带着这三个问题，我们看一下回归树模型及算法。
这里可以帮助解决第一个问题，公式5.16反映了回归树模型的基本模式。决策树建树的过程，对应了特征空间的划分，划分成的每个子空间，能够安放具有相同特征的数据实例，给他们具体的类别标记。在回归问题上，划分后的子空间单元同样可以用来表示回归模型的输出值。详细看一下公式5.16，指示函数部分表示，属于Rm类时，该值为1，用回归树模型进行预测时，属于该子空间的实例，赋予输出值为Cm。注意该公式的求和函数部分，输入数据x遍历每个子空间单元，遍历到所属的子空间后，得到输出值Cm，遍历其它子空间时不得值（因为指示函数条件不满足时，值为0），f(x)=0+0+…+Cm+…+0=Cm。
该部分提出了平方误差的计算思路，用于衡量训练数据的预测误差很好理解；用于求解每个单元上的最优输出值，类似于分类树中选择实例数量最多的类，目的在于找到该单元所代表的最优值。为什么均值会是最优值？原因就在于平方误差函数，取均值时，与其它值做差，方差最小。
这里可以帮助解决第二、三个问题，采取什么准则对什么进行选择。书中描述为，选取合适的变量（第几个实例）作为切分变量，其值为切分点。也就是说用第n个变量的值来划分特征空间，并且采用平方误差来作为切分点的选择标准。公式5.19很好理解，首先明确该公式希望找到最优的切分变量和最优切分点，此时误差值最小；中括号里分成了两部分，也就是切分点s两侧的情况；我们要使总误差值最小，就要使中括号中s左右两侧的误差都保持最小；先看左侧部分（R1），我们要找到合适的输出值c1使该项误差最小；实际上，左侧部分最合适的c1就是左侧部分所有yi的均值；右侧同理。
公式5.20表示的过程，我们很难直接计算出来，但我们可以采用遍历的笨方法，把所有的输入变量遍历一遍，去找最优的切分变量j。在遍历过程中，每个变量依次将特征空间划分为两个区域，对每个区域重复上述划分过程，直到满足停止条件未知。也就是下边的最小二乘回归树生成算法。
CART剪枝
该部分一个大公式，需要深入学习下~开学后整起。
代码效果
