问题:
对杨辉三角进行一些改造,每个位置的数字可以随意填写,经过某个数字只能到达下面一层相邻的两个数字。现在站在第一层往下移动,我们把移动到最底层所经过的所有数字之和
定义为路径的长度,请求出从最高层到最底层的最短路径。
三角如下:
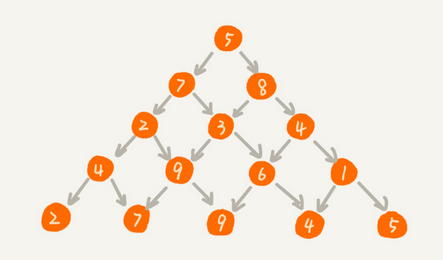
每一层对应一个阶段,每个阶段对应一个状态集合,问题的最优解包含子问题的最优解。包含重复字问题。例如,对于第三层的节点3,可能从7到达,也可能从8到达,这就是两个重复的子问题,我们可以用动态规划来合并重复的子问题从而减少状态数,选取达到当前节点路径最短的那个。
1 #include <iostream> 2 #include <string.h> 3 4 int main() 5 { 6 // 把三角形逆时针旋转 7 unsigned int value[5][5] = { 8 5, 0, 0, 0, 0, 9 7, 8, 0, 0, 0, 10 2, 3, 4, 0, 0, 11 4, 9, 6, 1, 0, 12 2, 7, 9, 4, 5 13 }; 14 15 // 每一层索引为i的节点可以到达下一层的i和i+1节点 16 17 unsigned int states[5][5] = {0}; 18 memset(states, 0xff, sizeof(int) * 5 * 5); 19 20 states[0][0] = 5; 21 22 for(int i = 0; i < 5 - 1; i++) // 循环到倒数第二层 23 { 24 for(int j = 0; j <= i; j++) 25 { 26 if(states[i][j] + value[i + 1][j] < states[i + 1][j]) 27 states[i + 1][j] = states[i][j] + value[i + 1][j]; 28 if(states[i][j] + value[i + 1][j+1] < states[i + 1][j + 1]) 29 states[i + 1][j + 1] = states[i][j] + value[i + 1][j+1]; 30 } 31 } 32 33 unsigned int min_value = 0xffffffff; 34 for(int i = 0; i < 5; i++) 35 if(states[4][i] < min_value) 36 min_value = states[4][i]; 37 38 std::cout << "min : " << min_value << std::endl; 39 40 return 0; 41 }
运行结果:
