学习目标
- 讨论有向图和无向图
- 定义带权图并讨论它们的应用
- 定义图的广度优先遍历和深度优先遍历
- 定义最小生成树
- 讨论图的实现策略
书中图的基本定义
- 图是由结点及结点间的连接组成的,结点称为顶点,结点间的连接称为边,顶点通常由名字或标号来表示,边由它所连接的顶点来表示。
无向图:
- 无向图中,表示边的顶点对是无序的,例如,标记顶点A,B,C,D,一条边可以表示为(A,B)。无向图表示顶点对是无序的,所以边(A,B)意味着A和B之间的连接是双向的,在一个无向图中,(A,B)和(B,A)所代表的边的含义完全一样。
- 如果图中两个顶点之间有边连接,则称这两个顶点是邻接的(邻居),自己连接到自己的边称为自循环或悬挂。
- 含有最多条边的无向图称为完全图:Edges=(n-1)*n/2.
- 路径是连接图中两个顶点的边的序列,路径长度为路径所含边的数目(顶点个数减一)
- 如果无向图中任意两个顶点间都有路径,则无向图称为连通的。
- 第一个顶点和最后一个顶点是同一个顶点且没有重复边的路径,称为一个环。
有向图
- 顶点是有序对的图称为有向图,有向图的每条边都带有一个移动方向,这个方向有顶点的顺序指定,所以(A,B)表示只允许从A移动到B,但不允许另一个方向的移动。
- 树就是图,树的大部分工作是针对有向树。有向树是一个有向图。
带权图
- 带权图每条边都对应一个权值,也称之为网络,根据需要带权图可以是无向也可以是有向的。
- 对于带权图来说,使用由起始结点,结束点及权构成的三元组来表示每个边。
图的实现
书中关于图的介绍,感觉有点颠倒,书中先介绍常用的图算法:遍历和判断最小路径等,而后才是介绍了图的实现策略。所以在一开始的时候有点懵的。
邻接表
- 因为树就是图,所以实现图的最好方式也许是采用实现树已用过的机制。使用一组结点,每个结点包含一个元素及可能和链接其他结点的一个链表。
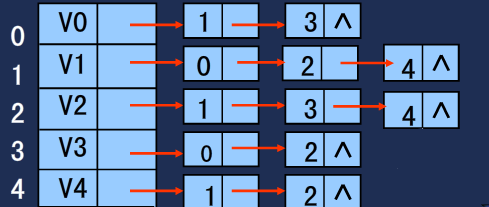
- 代码实现:僵硬!还未实现这个!请看下一个。
邻接矩阵
- 为了更好的表示结点与结点之间的关系,我们可以用二维数组来表示,也就是一个矩阵形式的表示方法。我们假设一个二维数组,它的顶点有:A ,B,C,D,E,那么数组中的一个元素aij不仅体现出了结点vi和结点vj的关系,而且aij的值正可以表示权值的大小。
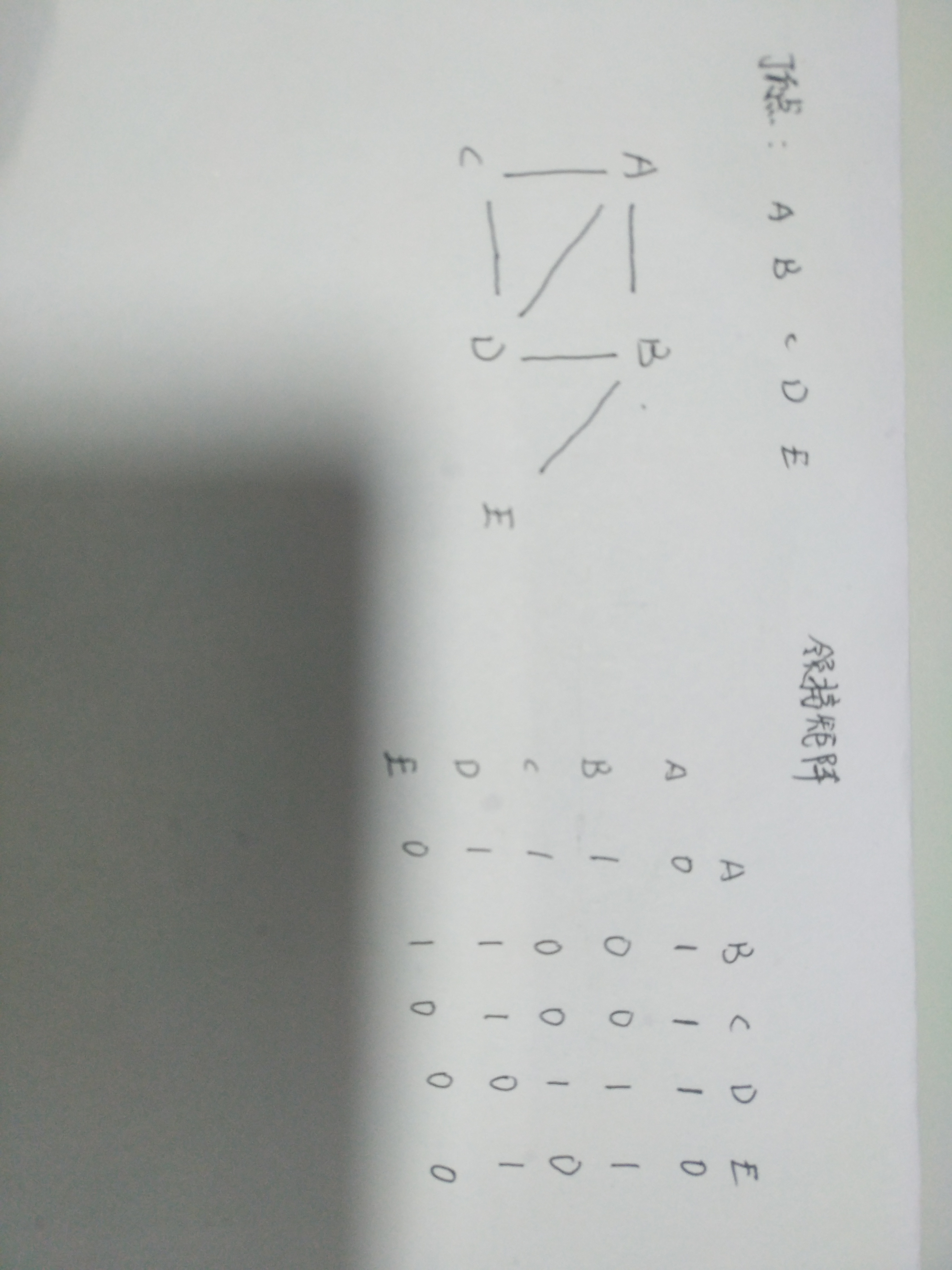
如果要让aij的值表示权值的话只需要将数值重新赋值就行。
- 算法实现