1,
复杂度:O (n log n)
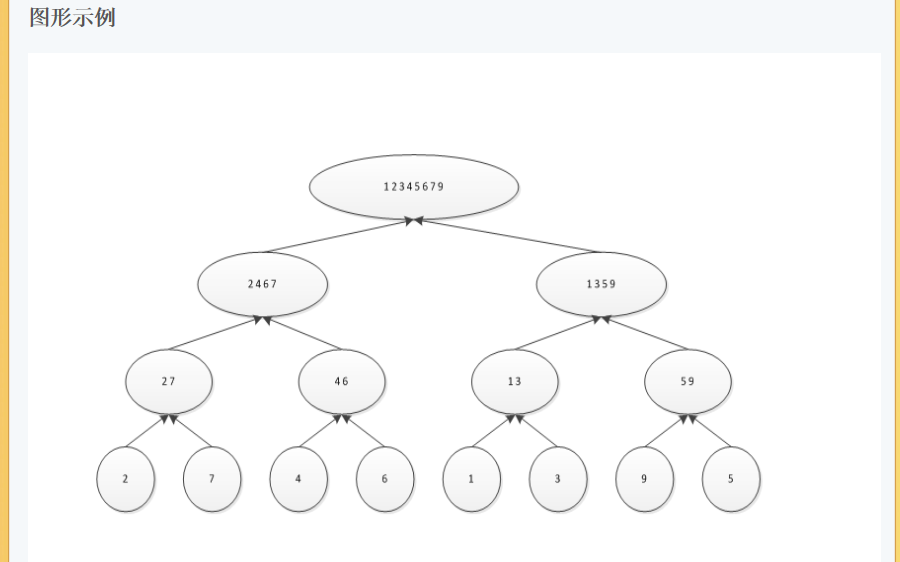
2路归并排序的基本思想:n个记录,看作n个有序子序列,每个子序列的长度为1,然后两两归并,得到n/2(向上取整)个长度为2或者1的有序子序列;再两两归并,......,如此重复,知道得到一个长度为n的有序序列位置。
#include <iostream> #include <stdio.h> #include <string.h> #include <stdlib.h> void merge(int array[], int low, int mid, int high) { int i, k; int *temp = (int *) malloc((high-low+1) * sizeof(int)); //申请空间,使其大小为两个 //已经排序序列之和,该空间用来存放合并后的序列 int begin1 = low; int end1 = mid; int begin2 = mid + 1; int end2 = high; for (k = 0; begin1 <= end1 && begin2 <= end2; ++k) //比较两个指针所指向的元素, //选择相对小的元素放入到合并空间,并移动指针到下一位置 { if(array[begin1]<=array[begin2]) { temp[k] = array[begin1++]; } else { temp[k] = array[begin2++]; } } if(begin1 <= end1) //若第一个序列有剩余,直接拷贝出来粘到合并序列尾 { memcpy(temp+k, array+begin1, (end1-begin1+1)*sizeof(int)); } if(begin2 <= end2) //若第二个序列有剩余,直接拷贝出来粘到合并序列尾 { memcpy(temp+k, array+begin2, (end2-begin2+1)*sizeof(int)); } memcpy(array+low, temp, (high-low+1)*sizeof(int));//将排序好的序列拷贝回数组中 free(temp); } void merge_sort(int array[], unsigned int first, unsigned int last) { int mid = 0; if(first<last) { /*mid = (first+last)/2;*/ /*注意防止溢出*/ /*mid = first/2 + last/2;*/ mid = (first & last) + ((first ^ last) >> 1); merge_sort(array, first, mid); merge_sort(array, mid+1,last); merge(array,first,mid,last); } } void print_content(int *a, int size) { for(int i=0;i<size;i++) { printf("%d ",a[i]); } printf(" "); } int main(void) { int a[]={10,17,18,19,13,14,15,11,12,16,21,20,23,22}; merge_sort(a,0,sizeof(a)/sizeof(a[0])); print_content(a,sizeof(a)/sizeof(a[0])); return 0; }
2,归并排序的前提是:归并前两个数组是有序的。归并排序的思路是先分成两半使用归并排序,然后比较大小,从小到大复制到一个零时数组中去;如果比较后,一方有剩余,那么将剩下的复制到临时数组,最后将排序好的数组拷贝回原数组。
归并排序的时间复杂度是:nlogn
#include<stdio.h> #include<stdlib.h> #define N 1000000 int array[N]; int temp[N]; void init_array(int a[],int n); void print_array(int a[],int n); void guibing_sort(int a[],int start,int end); void Guibing_sort(int a[],int n); int main() { init_array(array,N); Guibing_sort(array,N); print_array(array,N); } void init_array(int a[],int n) { int i; for(i=0;i<n;i++) a[i]=rand()%1000; } void print_array(int a[],int n) { int i; for(i=0;i<n;i++) printf("%d ",a[i]); } void guibing_sort(int a[],int start,int end) { int i,j,mid,k=0; if(start>=end) return ; mid=(start+end)/2; guibing_sort(a,start,mid); guibing_sort(a,mid+1,end); i=start; j=mid+1; while(i<=mid && j<=end)//比较从小到大放置 { if(a[i]<=a[j]) { temp[k++]=a[i++]; } else { temp[k++]=a[j++]; } } while(i<=mid) temp[k++]=a[i++]; while(j<=end) temp[k++]=a[j++];//如果有剩余则复制 for(i=0;i<k;i++) a[start+i]=temp[i];//拷贝回原数组 } void Guibing_sort(int a[],int n) { guibing_sort(a,0,n-1); }
2
基本思想:将元素集合分成2个集合,对每个集合单独分类,然后将已分类的两个序列归并成一个含有n个元素的分类好的序列。这种思想是典型的分治法的设计思想。
归并排序 #include <iostream> using namespace std; //元素交换 void swap(int &a,int &b) { int temp=a; a=b; b=temp; } /*/////////////////////////////////////////////// 归并排序 */ void Merge(int *a,int low,int mid,int high) { int b[100]; int l=low; int h=mid+1; int i=low; int j; while( l<=mid && h<=high ) //当分成的独立的两部分各自未超过范围时,比较元素,赋值给数组b中相应的元素 { if(a[l]<=a[h]) b[i++]=a[l++]; else b[i++]=a[h++]; } if(l>mid) //当超出范围,判断是哪一部分先超出,然后将剩余部分直接添加到数组b中 for(j=h;j<=high;j++) b[i++]=a[j]; if(h>high) for(j=l;j<=mid;j++) b[i++]=a[j]; for(j=low;j<=high;j++) //重写数组a中元素 a[j]=b[j]; } void MergeSort(int *a,int low,int high) //递归,合并排序 { if(low<high) { int mid=(low+high)/2; MergeSort(a,low,mid); MergeSort(a,mid+1,high); Merge(a,low,mid,high); } } ///////////////////////////////////////////////// int main() { int n,i,a[20]; cout<<"请输入数组元素n:"<<endl; cin>>n; cout<<"请输入"<<n<<"个元素:"<<endl; for(i=0;i<n;i++) cin>>a[i]; MergeSort(a,0,n-1); for(i=0;i<n;i++) cout<<a[i]<<" "; cout<<endl; return 0; }
4,
C 归并排序 归并算法描述 1.申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列 2.设定两个指针,最初位置分别为两个已经排序序列的起始位置 3.比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置 4.重复步骤3直到某一指针达到序列尾 5.将另一序列剩下的所有元素直接复制到合并序列尾 示例代码 以下示例代码实现了归并操作。arr是元素序列,其中从索引p开始到q位置,按照升序排列,同时,从(q+1)到r也已经按照升序排列,merge()函数将把这两个已经排序好的子序列合并成一个排序序列。结果放到arr中。 复制代码 1 #include <stdio.h> 2 #include <stdlib.h> 3 #include <string.h> 4 5 void merge(int arr[], int low, int mid, int high) 6 { 7 int j, k; 8 int begin1 = low; 9 int end1 = mid; 10 int begin2 = mid + 1; 11 int end2 = high; 12 13 int *temp = (int *) malloc((high - low + 1) * sizeof(int)); 14 15 for(k = 0; begin1 <= end1 && begin2 <= end2; ++ k) { 16 if(arr[begin1] <= arr[begin2]) 17 temp[k] = arr[begin1++]; 18 else temp[k] = arr[begin2++]; 19 } 20 21 if(begin1 <= end1) 22 //include <string.h> memcpy 23 memcpy(temp + k, arr + begin1, (end1 - begin1 + 1) * sizeof(int)); 24 if(begin2 <= end2) 25 memcpy(temp + k, arr + begin2, (end2 - begin2 + 1) * sizeof(int)); 26 memcpy(arr + low, temp, (high - low + 1) * sizeof(int)); 27 free(temp); 28 } 复制代码 归并排序 归并排序具体工作原理如下(假设序列共有n个元素): 1.将序列每相邻两个数字进行归并操作,形成floor(n / 2)个序列,排序后每个序列包含两个元素 2.将上述序列再次归并,形成floor(n / 4)个序列,每个序列包含四个元素 3.重复步骤2,直到所有元素排序完毕 示例代码 示例代码为C语言,输入参数中,需要排序的数组为arr[],起始索引为first,终止索引为last。调用完成后,arr[]中从first到last处于升序排列。 复制代码 1 int *merge_sort(int arr[], unsigned int first, unsigned int last) 2 { 3 int mid = 0; 4 if(first < last) { 5 mid = (first & last) + ((first ^ last) >> 1); 6 if(first < last) { 7 mid = (first & last) + ((first ^ last) >> 1); 8 merge_sort(arr, first, mid); 9 merge_sort(arr, mid+1, last); 10 merge(arr, first, mid, last); 11 } 12 return arr; 13 } 14 } 15 16 int main() 17 { 18 int arr[] = {2,7,4,6,1,3,9,5}; 19 int *result = merge_sort(arr, 0, 7); 20 int i = 0; 21 for(i = 0; i< 8 ; i++) { 22 printf("value %d ", *result); 23 result ++; 24 } 25 } 复制代码 输出结果 复制代码 value 1 value 2 value 3 value 4 value 5 value 6 value 7 value 9 复制代码 算法分析 比较操作的次数介于(nlogn) / 2和nlogn − n + 1。 赋值操作的次数是(2nlogn)。 归并算法的空间复杂度为:Θ (n)