Body Frame 方向向量采用单位向量, X_A=[1 0 0]' ,Y_A=[0 1 0]', Z_A=[0 0 1]'
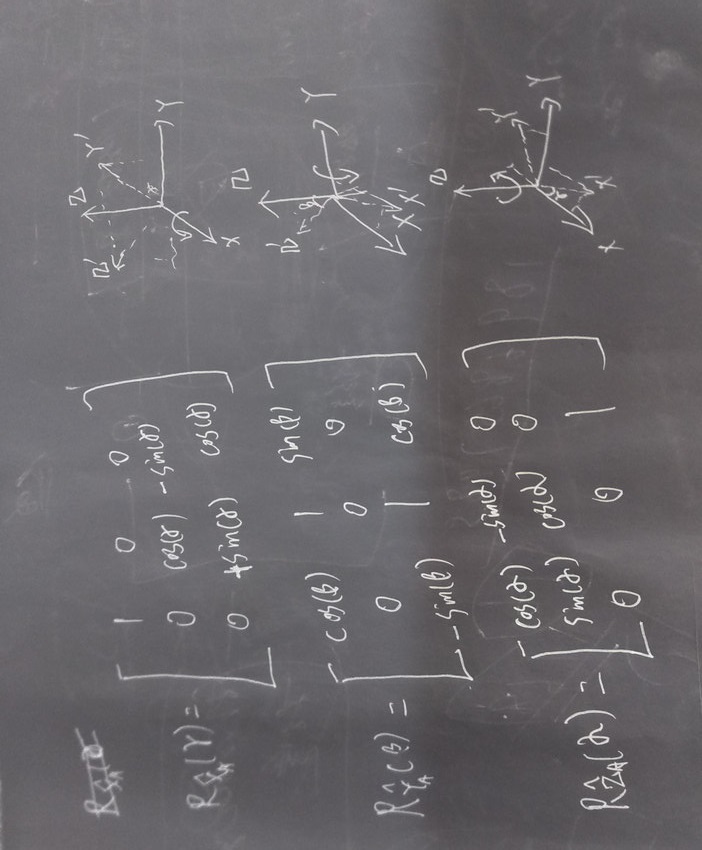
旋转矩阵的几点注意: 对角线上多是cos ,cos不分正负, 角度取-theta后,就变成原来的反矩阵,由于旋转矩阵是正交矩阵,所以其反矩阵也是 转置矩阵。
对A 对 B的旋转矩阵 R , 与 B对A的旋转矩阵互为反矩阵。 明显A对A的旋转矩阵R,就是转角是0的矩阵,代入0后明显发现就是单位矩阵, 所以对角线必需是cos, 只有cos(0)=1
//===================================================================
旋转矩阵与转移矩阵的3个用处
1.描述:Description: 一个Frame B 相对Frame A的 位置(指B org --原点在A坐标系下的向量),与 姿态。
2.Mapping :一个在Frame B下的位姿(位置与姿态) 变换成 Frame A下的位姿
3.Operator : 一个在Frame A下的位置,做位姿变换(转动与移动)
Fix angels : 对应Operator操作,采用Premultiply T3T2T1 v 对v来说是先T1再T2再T3,
Euler angels : 对应Mapping 操作 ,采用Postmultiply T1T2T3 v

prismatic
revolute