多元回归比一元回归优越性

 

python机器学习-乳腺癌细胞挖掘（博主亲自录制视频）

https://study.163.com/course/introduction.htm?courseId=1005269003&utm_campaign=commission&utm_source=cp-400000000398149&utm_medium=share

 

 

貌似一个不相关的变量，可能对结果有显著影响

多元回归可以分析独立变量与因变量是否显著相关。但解释能力不如因子分析

因子分析对变量相关性解释能力更强

 

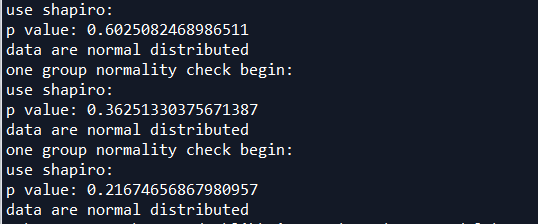
正态分布检验OK

三组数据呈现正态分布，可以用回归检测

# -*- coding: utf-8 -*-
'''
Author：Toby
QQ：231469242，all right reversed,no commercial use
normality_check.py
正态性检验脚本
  
'''
  
import scipy
from scipy.stats import f
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
# additional packages
from statsmodels.stats.diagnostic import lillifors
  
#对一列数据进行正态分布测试
def check_normality(testData):
    print("one group normality check begin:")
    #20<样本数<50用normal test算法检验正态分布性
    if 20<len(testData) <50:
       p_value= stats.normaltest(testData)[1]
       if p_value<0.05:
           print("use normaltest")
           print("p value:",p_value)
           print ("data are not normal distributed")
           return  False
       else:
           print("use normaltest")
           print("p value:",p_value)
           print ("data are normal distributed")
           return True
      
    #样本数小于50用Shapiro-Wilk算法检验正态分布性
    if len(testData) <50:
       p_value= stats.shapiro(testData)[1]
       if p_value<0.05:
           print ("use shapiro:")
           print("p value:",p_value)
           print ("data are not normal distributed")
           return  False
       else:
           print ("use shapiro:")
           print("p value:",p_value)
           print ("data are normal distributed")
           return True
        
    if 300>=len(testData) >=50:
       p_value= lillifors(testData)[1]
       
       if p_value<0.05:
           print ("use lillifors:")
           print("p value:",p_value)
           print ("data are not normal distributed")
           return  False
       else:
           print ("use lillifors:")
           print("p value:",p_value)
           print ("data are normal distributed")
           return True
      
    if len(testData) >300:
       p_value= stats.kstest(testData,'norm')[1]
       if p_value<0.05:
           print ("use kstest:")
           print("p value:",p_value)
           print ("data are not normal distributed")
           return  False
       else:
           print ("use kstest:")
           print("p value:",p_value)
           print ("data are normal distributed")
           return True
    #测试结束
    print("-"*100)
  
#对所有样本组进行正态性检验
def NormalTest(list_groups):
    for group in list_groups:
        #正态性检验
        status=check_normality(group)
        if status==False :
            return False
              
 

group1=[5,2,4,2.5,3,3.5,2.5,3]
group2=[1.5,2,1.5,2.5,3.3,2.3,4.2,2.5]
group3=[96,90,95,92,95,94,94,94]
list_groups=[group1,group2,group3]
list_total=group1+group2+group3
#对所有样本组进行正态性检验  
NormalTest(list_groups)

　　

下图可见，独立变量x1和x2没有相关，R调整平方为0.19

x1和yR调整平方0.59的关系--存在很弱关系

x2和y存在R调整平方-0.19，即没有关系

但x1和x2与y存在0.886R调整平方关系，非常强

且x1和x2与y结合后，残差服从正态分布，AIC和BIC值很小，

prob (F-statistic)=0.00187,小于0.05，说明回归方程显著

参数t检验显著，x1和x2的t分数P值分别为0.001和0.01,小于0.05，否定H0，表示x1和x2显著，说明此模型拟合度很好

说明貌似一个不相关的变量，可能对结果有显著影响

# -*- coding: utf-8 -*-
"""
Created on Tue Jul 18 09:37:15 2017

@author: toby
"""



# Import standard packages
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from sklearn import datasets, linear_model
from matplotlib.font_manager import FontProperties 
font_set = FontProperties(fname=r"c:windowsfontssimsun.ttc", size=15)  
# additional packages
import sys
import os
sys.path.append(os.path.join('..', '..', 'Utilities'))

try:
# Import formatting commands if directory "Utilities" is available
    from ISP_mystyle import showData 
    
except ImportError:
# Ensure correct performance otherwise
    def showData(*options):
        plt.show()
        return

# additional packages ...
# ... for the 3d plot ...
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm

# ... and for the statistic
from statsmodels.formula.api import ols
#生成组合
from itertools import combinations

x1=[5,2,4,2.5,3,3.5,2.5,3]
x2=[1.5,2,1.5,2.5,3.3,2.3,4.2,2.5]
y=[96,90,95,92,95,94,94,94]


#自变量列表
list_x=[x1,x2]

#绘制多元回归三维图
def Draw_multilinear():
    
    df = pd.DataFrame({'x1':x1,'x2':x2,'y':y})
    # --- >>> START stats <<< ---
    # Fit the model
    model = ols("y~x1+x2", df).fit()
    param_intercept=model.params[0]
    param_x1=model.params[1]
    param_x2=model.params[2]
    rSquared_adj=model.rsquared_adj
    
    #generate data,产生矩阵然后把数值附上去
    x = np.linspace(-5,5,101)
    (X,Y) = np.meshgrid(x,x)
    
    # To get reproducable values, I provide a seed value
    np.random.seed(987654321)   
    Z = param_intercept + param_x1*X+param_x2*Y+np.random.randn(np.shape(X)[0], np.shape(X)[1])

    # 绘图
    #Set the color
    myCmap = cm.GnBu_r
    # If you want a colormap from seaborn use:
    #from matplotlib.colors import ListedColormap
    #myCmap = ListedColormap(sns.color_palette("Blues", 20))
    
    # Plot the figure
    fig = plt.figure("multi")
    ax = fig.gca(projection='3d')
    surf = ax.plot_surface(X,Y,Z, cmap=myCmap, rstride=2, cstride=2, 
        linewidth=0, antialiased=False)
    ax.view_init(20,-120)
    ax.set_xlabel('X')
    ax.set_ylabel('Y')
    ax.set_zlabel('Z')
    ax.set_title("multilinear with adj_Rsquare %f"%(rSquared_adj))
    fig.colorbar(surf, shrink=0.6)
    
    outFile = '3dSurface.png'
    showData(outFile)

    
#检查独立变量之间共线性关系
def Two_dependentVariables_compare(x1,x2):
    # Convert the data into a Pandas DataFrame
    df = pd.DataFrame({'x':x1, 'y':x2})
    # Fit the model
    model = ols("y~x", df).fit()
    rSquared_adj=model.rsquared_adj
    print("rSquared_adj",rSquared_adj)
    if rSquared_adj>=0.8:
        print("high relation")
        return True
    elif 0.6<=rSquared_adj<0.8:
         print("middle relation")
         return False
    elif rSquared_adj<0.6:
         print("low relation")
         return False

#比较所有参数，观察是否存在多重共线
def All_dependentVariables_compare(list_x):  
    list_status=[]
    list_combine=list(combinations(list_x, 2))
    for i in list_combine:
        x1=i[0]
        x2=i[1]
        status=Two_dependentVariables_compare(x1,x2)
        list_status.append(status)
    if True in list_status:
        print("there is multicorrelation exist in dependent variables")
        return True
    else:
        return False
    
        
#回归方程，支持哑铃变量
def regressionModel(x1,x2,y):
    '''Multilinear regression model, calculating fit, P-values, confidence intervals etc.'''
    # Convert the data into a Pandas DataFrame
    df = pd.DataFrame({'x1':x1,'x2':x2,'y':y})
    
    # --- >>> START stats <<< ---
    # Fit the model
    model = ols("y~x1+x2", df).fit()
    # Print the summary
    print((model.summary()))
    return model._results.params  # should be array([-4.99754526,  3.00250049, -0.50514907])

    
# Function to show the resutls of linear fit model
def Draw_linear_line(X_parameters,Y_parameters,figname,x1Name,x2Name):
    #figname表示图表名字，用于生成独立图表fig1 = plt.figure('fig1')，fig2 = plt.figure('fig2')
    plt.figure(figname)
    #获取调整R方参数    
    df = pd.DataFrame({'x':X_parameters, 'y':Y_parameters})
    # Fit the model
    model = ols("y~x", df).fit()
    rSquared_adj=model.rsquared_adj 
    
    #处理X_parameter1数据
    X_parameter1 = []
    for i in X_parameters:
        X_parameter1.append([i])
    
    # Create linear regression object
    regr = linear_model.LinearRegression()
    regr.fit(X_parameter1, Y_parameters)
    plt.scatter(X_parameter1,Y_parameters,color='blue',label="real value")
    plt.plot(X_parameter1,regr.predict(X_parameter1),color='red',linewidth=4,label="prediction line")
    plt.title("linear regression %s and %s with adj_rSquare:%f"%(x1Name,x2Name,rSquared_adj))
    plt.xlabel('x', fontproperties=font_set)  
    plt.ylabel('y', fontproperties=font_set)  
    plt.xticks(())
    plt.yticks(())
    plt.legend()
    plt.show()      
    

#绘制多元回归三维图
Draw_multilinear()  
#比较所有参数，观察是否存在多重共线
All_dependentVariables_compare(list_x)              
Draw_linear_line(x1,x2,"fig1","x1","x2")
Draw_linear_line(x1,y,"fig4","x1","y")
Draw_linear_line(x2,y,"fig5","x2","y")
regressionModel(x1,x2,y)

    
    
'''
训练数据
x1=[2,6,8,3,2,7,9,8,4,6]
x2=[1,0,1,0,1,1,0,0,1,1]
y=[2900,3000,4800,1800,2900,4900,4200,4800,4400,4500]

x=[89,66,78,111,44,77,80,66,109,76]
y=[4,1,3,6,1,3,3,2,5,3]
z=[7,5.4,6.6,7.4,4.8,6.4,7,5.6,7.3,6.4]

x1=[89,66,78,111,44,77,80,66,109,76]
x2=[4,1,3,6,1,3,3,2,5,3]
x3=[3.84,3.19,3.78,3.89,3.57,3.57,3.03,3.51,3.54,3.25]
y=[7,5.4,6.6,7.4,4.8,6.4,7,5.6,7.3,6.4]

   
'''    

python信用评分卡建模（附代码，博主录制）

https://study.163.com/course/introduction.htm?courseId=1005214003&utm_campaign=commission&utm_source=cp-400000000398149&utm_medium=share