规则
单身妹妹到了适婚年龄,要选对象。候选男子100名,都是单身妹妹没有见过的。百人以随机顺序,从单身妹妹面前逐一经过。每当一位男子在单身妹妹面前经过时,单身妹妹要么选他为配偶,要么不选。如果选他,其余那些还没有登场的男子就都遣散回家,选配偶的活动也 over 了。如果不选,当下这名男子就离开,也就是 pass 掉此人,下一人登场。被pass 掉的,单身妹妹不可以反悔再从选。规则是,单身妹妹必须在这百人中选出一人做配偶,也就是说,如果前99人单身妹妹都看不中的话,她必须选择第100名男子为配偶,不管他有多么丑陋。
任务
给单身妹妹设计选择方法,让她有最高概率选到百人中最英俊的男子为配偶。说明一点是,没有任何选择方法能够保证单身妹妹一定选择到最帅的帅哥。对于任何选择方法,总存在某些出场的顺序,让单身妹妹与帅哥错过。所以,题目所问的,不是必胜的选法(因为不存在),而是概率最高的选法。
算法
因为并不是要讨论数学,我这里就直接给出答案了:最佳选法是 pass 掉最开始的 100/e 名男子(e = 2.718… 是自然对数,即 100/e 约等于 37)。但是记录下这 37 名男子中最英俊者。之后鱼贯而来的男子中,出现的第一位英俊程度超越所有前 37 人者,即为配偶。如果人都走光了,也没出现这么一位 Mr. Right,那么就只好选择第 100 位男子。
如果你是这百名男子中的一名,并且你能够决定自己出场的名次,你会选择在什么时候出场,以最大提高自己被选的概率?
答案是第 38 名。你不会选择在38名之前,因为你被选的概率是零(假设我们的单身妹妹学过高等数学,知道最佳选法)。你也不会选择后于38,因为你前面每多一个人,就意味着多了一分单身妹妹选上他的机会。
如果你有一位意中人,你当然要努力去追求幸福,但你可能也要想一下,这是否是最好的时机?
37% 法则“实测”!
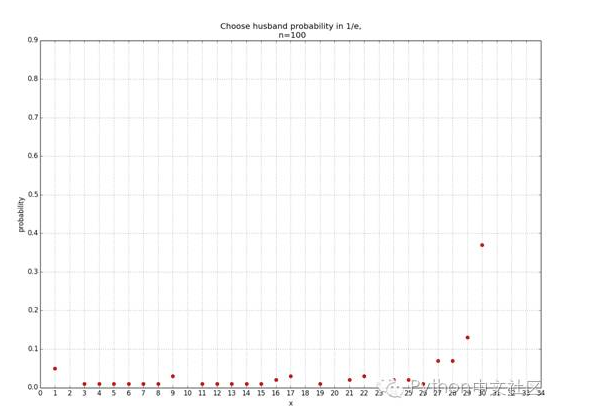
37% 法则的效果究竟如何呢?我们在计算机上编写程序模拟了当 n = 30 时利用 37% 法则进行选择的过程(如果MM始终未接受求爱者,则自动选择最后一名求爱者)。编号越小的男生越次,编号为 30 的男生则表示最佳选择。程序运行 10000 次之后,竟然有大约 4000 次选中最佳男生,可见 37% 法则确实有效啊。
建模测试图
变了几个参数试验次数n,number配偶人数,但结果相同,最优秀的30号配偶被选中概率最高。
e确实是宇宙数,e无所不在。。。
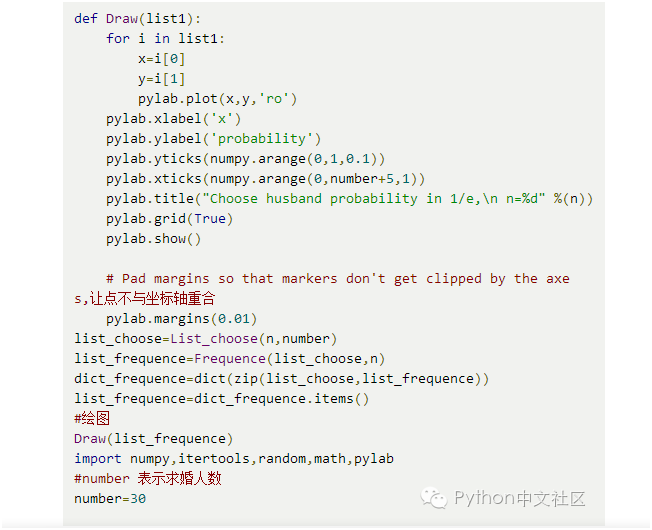
我们用python来建模,以下是全部代码。这里要导入numpy,math模块用于数学计算。Pylab用于数据可视化。Random模板用于产生随机数。
建模代码






End.