python机器学习-乳腺癌细胞挖掘(博主亲自录制视频)https://study.163.com/course/introduction.htm?courseId=1005269003&utm_campaign=commission&utm_source=cp-400000000398149&utm_medium=share
原创作者toby,机器学习,统计项目联系QQ:231469242
学生t-分布可简称为t分布。其推导由威廉·戈塞于1908年首先发表,当时他还在都柏林的健力士酿酒厂工作。因为不能以他本人的名义发表,所以论文使用了学生(Student)这一笔名。之后t检验以及相关理论经由罗纳德·费雪的工作发扬光大,而正是他将此分布称为学生分布。
要理解此文章,需要理解正太分布的基础知识,否则不能看懂。根据大数定理,样本越多,样本估算参数就越接近总体参数。但实际生活中,因为时间和费用,我们一般用小样本数据代替整体数据。
T分布的特征|:
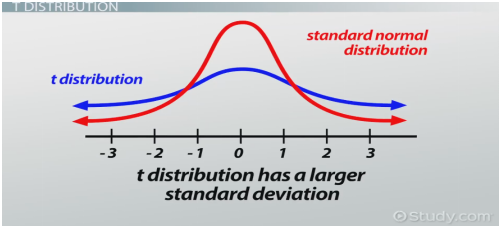
T分布属性1:曲线下面总面积为1
T分布属性2:曲线以0为对称中心,比正态分布更加扁平
T分布属性3:曲线向左右方向无限延伸,但没有碰到x轴
T分布属性4:自由度增加时(样本增加),T分布接近正态分布,T分布拥有更大标准差。如果样本数量大于30,数据分布近似正态分布;如果样本量小于30,数据分布呈T分布

自由度是一个非常复杂的概念,很多专业人士避而不谈自由度。简单理解,T分布的自由度=样本量-1

Z分数公式到t分数公式 ,如果样本数量大于30,用正态分布公式;如果样本量小于30,用T分布公式
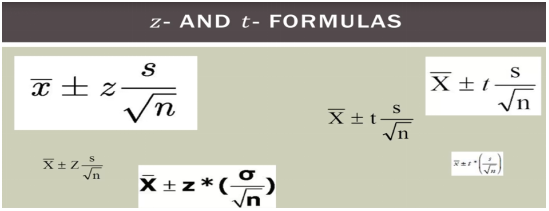
经过大量图文讲解,我们知道了T分布的基础知识。接下来我们了解T分布在医药领域用途。

T分布在医药领域有广泛用途,因为临床实验有0-4期,跨越时间长达数年,花费高(上亿)。临床实验每一期需要大量资金投入,病人样本量越多,药企花费越高。如果样本量小于30时,我们可以采用T分布分析。所以T分布在医药领域很受欢迎,因为可以节约大量开支。
⑴Ⅰ期临床试验:是在人体进行新药研究的起始期,主要目的是研究人对新药的耐受程度,了解新药在人体内的药代动力学过程,提出新药安全有效的给药方案。对象:健康人。
⑵II期临床试验:为随机盲法对照临床试验,由药物临床试验机构进行临床试验。其目的是确定药物的疗效适应证,了解药物的毒副反应,对该药的有效性、安全性作出初步评价。对象:靶疾病的患者。
⑶Ⅲ期临床试验:是Ⅱ期临床试验的延续,目的是在较大范围内进行新药疗效和安全性评价。要求在Ⅱ期临床试验的基 础上除增加临床试验的病例数之外,还应扩大临床试验单位。多中心临床试验单位应在临床药理基地中选择,一般不少于3个,每个中心病例数不少于20例。各项 要求与II期相似,但一般不要求双盲医学|教育网搜集整理。
⑷Ⅳ期临床试验:也称上市后监察。其目的在于进一步考查新药的安全有效性,即在新药上市后,临床广泛使用的最初 阶段,对新药的疗效、适应证、不良反应、治疗方案可进一步扩大临床试验,以期对新药的临床应用价值做出进一步评价,进一步了解的疗效、适应证与不良反应情 况,指导临床合理用药。包括扩大试试验、特殊对象临床试验、补充临床试验。
举一个例子,有七个病人,服用增加血压的新药3个月。他们血压分别升高了1.5, 2.9, 0.9, 3.9, 3.2, 2.1, 1.9,预测95%置信度的总体患者血压值的置信区间。
计算T分布需要用T-分数表

看T分布表有点麻烦,为了简单和避免出错,我已经用python代码封装好。
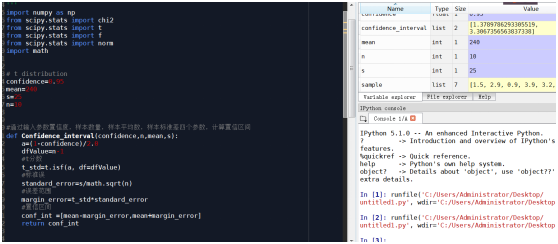
只需要输入参数(样本和置信度)样本:[1.5,2.9,0.9,3.9,3.2,2.1,1.9],置信度:0.95
程序自动得到结果[1.3789786293305519, 3.3067356563837338]
程序回答了上述问题,在95%置信度的条件下,总体患者血压值的置信区间为1.3789786293305519和3.3067356563837338之间

环境:Anaconda(python2.7)
下面代码经过测试,可以运行。
代码属于手动建模,scipy.stats.t.interval也可以准确计算T分布的置信区间,代码量更少,但少了一份自己建模的乐趣。
# -*- coding: utf-8 -*-
'''
T分布建模
'''
import numpy as np
from scipy.stats import chi2
from scipy.stats import t
from scipy.stats import f
from scipy.stats import norm
import math
# t distribution
confidence=0.95
mean=240
s=25
n=10
#通过输入参数置信度,样本数量,样本平均数,样本标准差四个参数,计算置信区间
def Confidence_interval(confidence,n,mean,s):
a=(1-confidence)/2.0
dfValue=n-1
#t分数
t_std=t.isf(a, df=dfValue)
#标准误
standard_error=s/math.sqrt(n)
#误差范围
margin_error=t_std*standard_error
#置信区间
conf_int =[mean-margin_error,mean+margin_error]
return conf_int
sample=[1.5,2.9,0.9,3.9,3.2,2.1,1.9]
def Confidence_interval2(sample,confidence):
a=(1-confidence)/2.0
#样本数量
n=len(sample)
#平均数
mean=np.mean(sample)
s=np.std(sample,ddof=1)
#自由度
dfValue=n-1
#t分数
t_std=t.isf(a, df=dfValue)
#标准误
standard_error=s/math.sqrt(n)
#误差范围
margin_error=t_std*standard_error
#置信区间
conf_int =[mean-margin_error,mean+margin_error]
return conf_int
confidence_interval=Confidence_interval2(sample,confidence)