地址:http://codeforces.com/contest/801/problem/D
题目:
You are given a convex polygon P with n distinct vertices p1, p2, ..., pn. Vertex pi has coordinates (xi, yi) in the 2D plane. These vertices are listed in clockwise order.
You can choose a real number D and move each vertex of the polygon a distance of at most D from their original positions.
Find the maximum value of D such that no matter how you move the vertices, the polygon does not intersect itself and stays convex.
The first line has one integer n (4 ≤ n ≤ 1 000) — the number of vertices.
The next n lines contain the coordinates of the vertices. Line i contains two integers xi and yi ( - 109 ≤ xi, yi ≤ 109) — the coordinates of the i-th vertex. These points are guaranteed to be given in clockwise order, and will form a strictly convex polygon (in particular, no three consecutive points lie on the same straight line).
Print one real number D, which is the maximum real number such that no matter how you move the vertices, the polygon stays convex.
Your answer will be considered correct if its absolute or relative error does not exceed 10 - 6.
Namely, let's assume that your answer is a and the answer of the jury is b. The checker program will consider your answer correct if  .
.
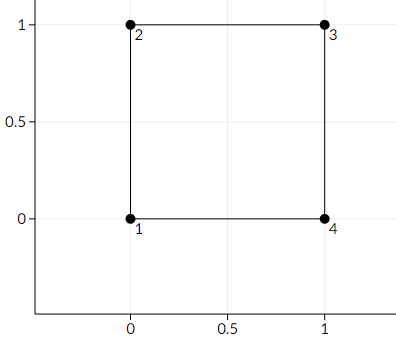
4
0 0
0 1
1 1
1 0
0.3535533906
6
5 0
10 0
12 -4
10 -8
5 -8
3 -4
1.0000000000
Here is a picture of the first sample
Here is an example of making the polygon non-convex.
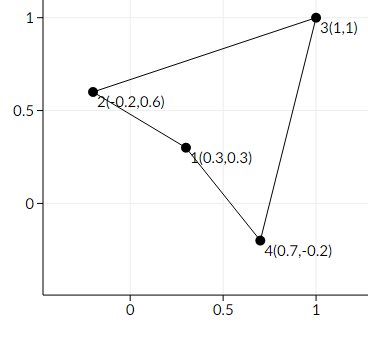
This is not an optimal solution, since the maximum distance we moved one point is ≈ 0.4242640687, whereas we can make it non-convex by only moving each point a distance of at most ≈ 0.3535533906.
思路:这题看起来很复杂,但是看下样例一的图后会发现一个结论:
在相邻的三个点a,b,c中,能移动的最大距离d就是b到直线ac的距离的一半。
证明:当d大于一半时,凸包会被破坏。
当d小于一半时,凸包仍然存在(即可以继续移动)

所以贴个求点到直线的模板,然后扫一遍所有点,求出所有可移动距离的最大值中的最小值即可。
(完整代码模板我博客有
1 #include <bits/stdc++.h>
2
3 using namespace std;
4
5 #define MP make_pair
6 #define PB push_back
7 typedef long long LL;
8 typedef pair<int,int> PII;
9 const double eps=1e-8;
10 const double pi=acos(-1.0);
11 const int K=1e6+7;
12 const int mod=1e9+7;
13
14
15 //点
16 class Point
17 {
18 public:
19 double x, y;
20
21 Point(){}
22 Point(double x, double y):x(x),y(y){}
23
24 bool operator < (const Point &_se) const
25 {
26 return x<_se.x || (x==_se.x && y<_se.y);
27 }
28 /*******判断ta与tb的大小关系*******/
29 static int sgn(double ta,double tb)
30 {
31 if(fabs(ta-tb)<eps)return 0;
32 if(ta<tb) return -1;
33 return 1;
34 }
35 static double xmult(const Point &po, const Point &ps, const Point &pe)
36 {
37 return (ps.x - po.x) * (pe.y - po.y) - (pe.x - po.x) * (ps.y - po.y);
38 }
39 friend Point operator + (const Point &_st,const Point &_se)
40 {
41 return Point(_st.x + _se.x, _st.y + _se.y);
42 }
43 friend Point operator - (const Point &_st,const Point &_se)
44 {
45 return Point(_st.x - _se.x, _st.y - _se.y);
46 }
47 //点位置相同(double类型)
48 bool operator == (const Point &_off) const
49 {
50 return Point::sgn(x, _off.x) == 0 && Point::sgn(y, _off.y) == 0;
51 }
52 //点位置不同(double类型)
53 bool operator != (const Point &_Off) const
54 {
55 return ((*this) == _Off) == false;
56 }
57 //两点间距离的平方
58 static double dis2(const Point &_st,const Point &_se)
59 {
60 return (_st.x - _se.x) * (_st.x - _se.x) + (_st.y - _se.y) * (_st.y - _se.y);
61 }
62 //两点间距离
63 static double dis(const Point &_st, const Point &_se)
64 {
65 return sqrt((_st.x - _se.x) * (_st.x - _se.x) + (_st.y - _se.y) * (_st.y - _se.y));
66 }
67 };
68 //两点表示的向量
69 class Line
70 {
71 public:
72 Point s, e;//两点表示,起点[s],终点[e]
73 double a, b, c;//一般式,ax+by+c=0
74
75 Line(){}
76 Line(const Point &s, const Point &e):s(s),e(e){}
77 Line(double _a,double _b,double _c):a(_a),b(_b),c(_c){}
78
79 //向量与点的叉乘,参数:点[_Off]
80 //[点相对向量位置判断]
81 double operator /(const Point &_Off) const
82 {
83 return (_Off.y - s.y) * (e.x - s.x) - (_Off.x - s.x) * (e.y - s.y);
84 }
85 //向量与向量的叉乘,参数:向量[_Off]
86 friend double operator /(const Line &_st,const Line &_se)
87 {
88 return (_st.e.x - _st.s.x) * (_se.e.y - _se.s.y) - (_st.e.y - _st.s.y) * (_se.e.x - _se.s.x);
89 }
90 friend double operator *(const Line &_st,const Line &_se)
91 {
92 return (_st.e.x - _st.s.x) * (_se.e.x - _se.s.x) - (_st.e.y - _st.s.y) * (_se.e.y - _se.s.y);
93 }
94 //从两点表示转换为一般表示
95 //a=y2-y1,b=x1-x2,c=x2*y1-x1*y2
96 bool pton()
97 {
98 a = e.y - s.y;
99 b = s.x - e.x;
100 c = e.x * s.y - e.y * s.x;
101 return true;
102 }
103
104 //-----------点和直线(向量)-----------
105 //点在向量左边(右边的小于号改成大于号即可,在对应直线上则加上=号)
106 //参数:点[_Off],向量[_Ori]
107 friend bool operator<(const Point &_Off, const Line &_Ori)
108 {
109 return (_Ori.e.y - _Ori.s.y) * (_Off.x - _Ori.s.x)
110 < (_Off.y - _Ori.s.y) * (_Ori.e.x - _Ori.s.x);
111 }
112
113 //点在直线上,参数:点[_Off]
114 bool lhas(const Point &_Off) const
115 {
116 return Point::sgn((*this) / _Off, 0) == 0;
117 }
118 //点在线段上,参数:点[_Off]
119 bool shas(const Point &_Off) const
120 {
121 return lhas(_Off)
122 && Point::sgn(_Off.x - min(s.x, e.x), 0) > 0 && Point::sgn(_Off.x - max(s.x, e.x), 0) < 0
123 && Point::sgn(_Off.y - min(s.y, e.y), 0) > 0 && Point::sgn(_Off.y - max(s.y, e.y), 0) < 0;
124 }
125
126 //点到直线/线段的距离
127 //参数: 点[_Off], 是否是线段[isSegment](默认为直线)
128 double dis(const Point &_Off, bool isSegment = false)
129 {
130 ///化为一般式
131 pton();
132
133 //到直线垂足的距离
134 double td = (a * _Off.x + b * _Off.y + c) / sqrt(a * a + b * b);
135
136 //如果是线段判断垂足
137 if(isSegment)
138 {
139 double xp = (b * b * _Off.x - a * b * _Off.y - a * c) / ( a * a + b * b);
140 double yp = (-a * b * _Off.x + a * a * _Off.y - b * c) / (a * a + b * b);
141 double xb = max(s.x, e.x);
142 double yb = max(s.y, e.y);
143 double xs = s.x + e.x - xb;
144 double ys = s.y + e.y - yb;
145 if(xp > xb + eps || xp < xs - eps || yp > yb + eps || yp < ys - eps)
146 td = min(Point::dis(_Off,s), Point::dis(_Off,e));
147 }
148
149 return fabs(td);
150 }
151 };
152
153 int n;
154 Point pt[K];
155 Line ta;
156 double ans=1e10;
157 int main(void)
158 {
159 cin>>n;
160 for(int i=1;i<=n;i++)
161 scanf("%lf%lf",&pt[i].x,&pt[i].y);
162 for(int i=1;i<=2;i++)
163 pt[i+n]=pt[i];
164 for(int i=1;i<=n;i++)
165 {
166 ta.s=pt[i],ta.e=pt[i+2];
167 ans=min(ans,ta.dis(pt[i+1])/2.0);
168 }
169 printf("%.8f
",ans);
170 return 0;
171 }