CF1480A Yet Another String Game
Problem
传送门CF1480A
给出一个字符串,两人轮流操作,每次操作可以将一个字符改为另外一个字符,当不可以不改动,先手目标是让最终字符串字典序最小,后手目标相反,求最终字符串。
Sol
贪心地模拟即可。
#define in read()
int read(){int x = 0,sgn = 1;char ch; for(;!isdigit(ch);ch=getchar())if(ch=='-')sgn=-1;for(;isdigit(ch);ch=getchar())x=(x<<1)+(x<<3)+(ch^48);return x*sgn;}
int main(){
int T = in;
while(T--){
char s[55];
scanf("%s",s+1); int n = strlen(s+1);
for(int i = 1;i <= n;i++){
if(i & 1) s[i] = s[i] == 'a' ? 'b' : 'a';
else s[i] = s[i] == 'z' ? 'y' : 'z';
}
printf("%s
",s+1);
}
return 0;
}
CF1480B The Great Hero
Problem
传送门CF1480B
有一个英雄,需要击败一堆怪物,他可以每次 1v1 地打怪物,英雄有两个属性,(A) (攻击力), (B) (血量),怪物也有两个属性 (a) , (b) (攻击、血量),每一轮战斗后,英雄血量扣除 (a) , 怪物血量扣除 (A) ,如果血量小于等于 (0) , 直接去世,问英雄最后能否杀死所有怪物。
注意:英雄可以选择击杀的顺序,在杀死所有怪物后,英雄可以牺牲(即可以同归于尽)。
Sol
按题意模拟打怪,但是英雄最后可以同归于尽,因此把攻击力最大的怪物弄到最后即可。
#define in read()
const int N = 1e5+10;
int n;
ll A,B;
struct mon{ll a,b;}al[N];
bool operator < (mon x,mon y){return x.a < y.a;}
void solve(){
for(int i = 1;i <= n;i++){
if(B <= 0){puts("NO");return;}
int tim = (al[i].b + A - 1) / A; //因为要杀死,所以向上取整
B -= tim * al[i].a;
if(B <= 0){
if(B + al[i].a > 0) continue;
puts("NO");return;
}
}puts("YES");
}
int main(){
int t = in;
while(t--){
A = in,B = in,n = in;
for(int i = 1;i <= n;i++) al[i].a = in;
for(int i = 1;i <= n;i++) al[i].b = in;
sort(al+1,al+n+1);
solve();
}
return 0;
}
CF1480C Searching Local Minimum
Problem
传送门CF1480C CF1479A
交互题,给你一个长度为 (n) ((leq 10^5))的序列 (A),你每次可以问一个位置的值,找出一个位置 (i) , 使得 (A[i]) < (min{A[i-1],A[i+1]}) ,((A[0],A[n+1] = inf)) , 你最多可以问 (100) 次。
Sol
先特判两端,然后考虑二分。
如果一个 (mid) 不行,一定是这样:
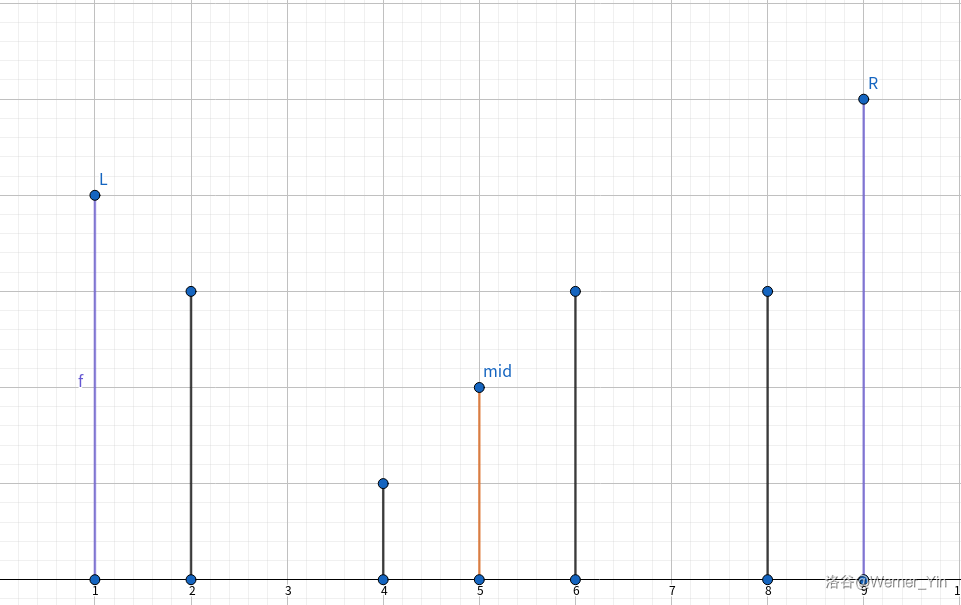
或者:
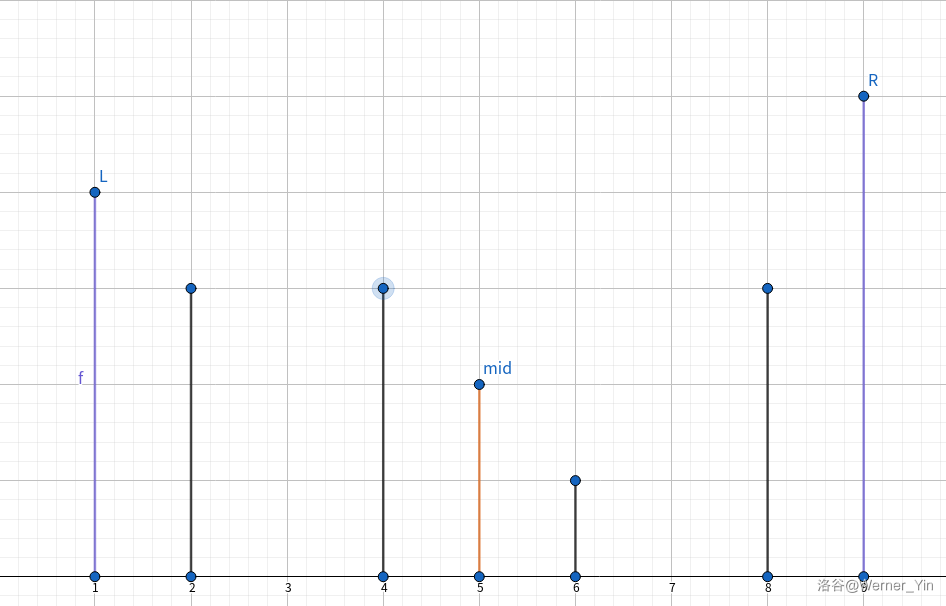
情况一,([l,mid-1]) 一定有答案,情况二,([mid+1,r]) 一定有答案。
二分就完了:
#define in read()
const int N = 1e5+10;
int a[N],n;
void Find(int x){printf("! %d
",x);fflush(stdout);exit(0);}
void query(int x){//记忆化
if(a[x]) return;
printf("? %d
",x);fflush(stdout);
a[x] = in;
}
bool able(int x){//check
query(x); query(x-1); query(x+1);
if(a[x] < min(a[x-1],a[x+1])) return 1;
return 0;
}
int main(){
n = in; a[0] = N+1,a[n+1] = N+1;
int l = 1,r = n;
if(able(l)) Find(l);
if(able(r)) Find(r);
while(l <= r){
int mid = l+r>>1;
if(able(mid)) Find(mid);
int lm = a[mid-1],rm = a[mid+1];
if(lm < rm) r = mid-1;
else l = mid+1;
}
Find(l);
return 0;
}
CF1480D1 Painting the Array I
Problem
upd : 2.22 修改了英文不好的错误。
对一个序列 (A) ($|A| <= 10^5 $)黑白染色,记一个位置上一个与它同色的位置为 (las)(没有则为 (0)),若 $las = 0 $ or $ a[las] eq a[i]$ , 你将的到一的贡献,求最大贡献。
Sol
看起来是贪心,然后 WA 了几发,因为想法太 naive 了。
比赛时自造的 (hack) 数据
7
2 2 2 1 3 2 2
(naive) 的做法:
int main(){
n = in;for(int i = 1;i <= n;i++) a[i] = in;
int tot = 0;
for(int i = 1;i <= n;i++){
if(en[0] == a[i]){
if(en[1] != a[i]) en[1] = a[i],tot++;
}else en[0] = a[i],tot++;
}printf("%d
",tot);
return 0;
}
直接被叉爆。
于是 又交了一个更 naive 的
考虑为什么被叉爆了:
问题就在如果一个位置两个末尾都可以选的情况,这个时候,就尽量帮后面一个位置增加贡献,改一改就行了。
#define in read()
const int N = 1e5+10;
int a[N],n,en[3];
int main(){
n = in;for(int i = 1;i <= n;i++) a[i] = in;
int tot = 1;
en[1] = a[1];
for(int i = 2;i <= n;i++){
if(a[i] != en[1]) {
tot++;
if(en[1] != a[i+1] && a[i] != en[2]) en[2] = a[i];
else en[1] = a[i];
}
else if(a[i] != en[2]) {
tot++; en[2] = a[i];
}
}printf("%d
",tot);
return 0;
}
CF1480D2 Painting the Array II
Problem
传送门CF1480D2 CF1479B2
对一个序列 (A) ($|A| <= 10^5 $)黑白染色,记一个位置上一个与它同色的位置为 (las)(没有则为 (0)),若 (las = 0 or a[las]
eq a[i]) , 你将的到一的贡献,求最 小 贡献。
Sol
WA 了 (inf) 发,一直没调出。
因为比赛的时候是 DP 解法,想讲 DP 的吧。
首先要去重,将 $a[i] = a[i-1] $ 的合并成一个数(因为没有贡献),设 (f[i]) 代表以 (i) 结尾最小贡献。
(f[i] = min{(f[p]+i-p-1+a[p-1] != a[i])},p in [1,i-1])
然后 (p) 有用的转移点一定不多,(p = i-1 space or space las[a[i]]+1) , (比赛时想到了,但是搞得有点复杂,不好合并,就一直WAWAWA)
#define in read()
// DP Sol
const int N = 1e5+10;
int n,a[N],f[N],en[N],val[N],las[N],m;
int main(){
n = in;
for(int i = 1;i <= n;i++) a[i] = in;
for(int i = 1;i <= n;i++) if(a[i] != a[m]) a[++m] = a[i];
int ans = m; f[1] = 1;las[a[1]] = 1;
for(int i = 2;i <= m;i++){
f[i] = f[i-1] + (a[i] != a[i-1]);
if(las[a[i]]){
int l = las[a[i]]+1;
f[i] = min(f[i],f[l]+i-l-1);
}
las[a[i]] = i;
ans = min(ans,f[i] + m - i);
}
printf("%d
",ans);
return 0;
}
当然,贪心的解法更妙。官方题解大概说此题就是 Bélády's algorithm。
大概就是记个 (nxt[i]) , 表示 (a[i]) 下一次出现的地方,类似于上一题,当一个数放在两个序列末尾时,都会有 1 的贡献时,我们优先放那个 (nxt) 更远的位置,因为(nxt) 更进的位置更加有 "活" 下来的机会使得贡献不增(感性理解吧)。
#define in read()
const int N = 1e5+10;
int n,a[N],en[2],nxt[N],p[N];
int main(){
n = in;
for(int i = 1;i <= n;i++) a[i] = in,p[a[i]] = N;
for(int i = n;i >= 1;i--) nxt[i] = p[a[i]],p[a[i]] = i;
int ans = 0; nxt[0] = N+1;
for(int i = 1;i <= n;i++){
if(a[en[1]] == a[i]) en[1] = i;
else if(a[en[0]] == a[i]) en[0] = i;
else{
if(nxt[en[0]] > nxt[en[1]]) en[0] = i;
else en[1] = i;
ans++;
}
}
printf("%d
",ans);
return 0;
}
CF1480E Continuous City
Problem
传送门CF1480E CF1479C
对一张 (n) 个点的有向图定义((L,R)) 连续为 : 从(1) 到 (n) 的每条路径中,长度为 (i in[L,R]) 的路径只出现一次。
给定 (L,R) ,求构造满足的图。
Sol
感觉挺妙的。
我们可以构造一个合法的解通过一下几步。
- (L = 1 ,R = 2 ^ k) 。
构造一排城市,对于编号为 (x,2 leq x leq k+2) 的城市,满足以它为终点的是一个 ((1,2^{x-2})) 连续图。
假设当前我们已经构造出来了一个 ((1,2^t)) 连续图,那么我们只要在加入一个新点 (t+3) ,并加边 ((1,t+3,1)) 、((x,t+3,2^{x-2})) ,这样就构造出来一个 ((1,2^{t+1})) 连续图
2.(L = 1,R) 不能表示为 (2^k) 。
那么,将 (R) 二进制拆分,设 (R-1 = sum_limits{i=0}^k R_i imes2^i) ,首先用步骤一构造出一张图,新建一个点 (x),加边((1,x,1)) ,然后对于每个 (R_i = 1) , 加边((i+2,x,1+sum_limits{j=i+1}^k R_i imes 2 ^ i)) ,自己画个图就知道了。
3.(L!=1)。
转化为问题((1,R-L+1)) , 然后新建点(x),加边 ((x-1,x,L-1)) , 即可。
#define in read()
struct edge{int u,v,w;};
vector<edge> e;
void link(int x,int y,int w){e.pb((edge){x,y,w});}
int solve(int L,int R){
if(L > 1){
int x = solve(1,R-L+1);
link(x,x+1,L-1);
return x+1;
}
if((R & -R) == R){
int tot = 2;
for(int i = 1;i <= R;i<<=1,tot++){
link(1,tot,1);
for(int j = 2;j < tot;j++) link(j,tot,1<<(j-2));
}
return tot - 1;
}
int num = 0;
for(;(1<<(num+1))<=(R-1);num++);
int x = solve(1,1<<num)+1;;
link(1,x,1);
for(int i = 0;i <= num;i++)
if((R-1) >> i & 1)
link(i+2,x,1+(R-1>>i+1<<i+1));
return x;
}
int main(){
int L = in, R = in;
int ans = solve(L,R);
printf("YES
%d %d
",ans,e.size());
for(int i = 0;i < e.size();i++) {
printf("%d %d %d
",e[i].u,e[i].v,e[i].w);
}
return 0;
}
总结
1.以后要多做构造题。
2.二进制拆分是一种解决构造题的好方法。
3.要多练贪心