在一些数学公式的推导中,常会遇到 (d) / (partial) / (delta) (Delta) 等符号。它们背后分别代表的数学含义?
增量
设变量 (u) 从它的一个初值 (u_1) 变到终值 (u_2),终值与初值的差 (u_2 - u_1) 就叫做变量 (u) 的增量,记作 (Delta u),即
增量 (Delta u) 可以是正的,也可以是负的。
应该注意到:记号 (Delta u) 并不表示某个量 (Delta) 与变量 (u) 的乘积,而是一个整体不可分割的记号。
举例:
现在假定函数 (y = f(x)) 在点 (x_0) 的某一个邻域内是有定义的。当自变量 (x) 在这个邻域内从 (x_0) 变到 (x_0 + Delta x) 时,函数值(或因变量) (f(x)) 相应地从 (f(x_0)) 变到 (f(x_0 + Delta x)),因此,函数值(或因变量) (f(x)) 的对应增量为
习惯上也称 (Delta y) 为函数的增量。
由此,可以定义函数的连续性,如下:
设函数 (y = f(x)) 在点 (x_0)) 的某一个邻域内有定义,如果
那么就称函数 (y = f(x)) 在点 (x_0) 连续。
导数
导数的定义: 设函数 (y = f(x)) 在点 (x_0) 的某个邻域内有定义,当自变量 (x) 在 (x_0) 处取得增量 (Delta x) (点 (x_0 + Delta x) 仍在该邻域内)时,相应地,因变量取得增量 (Delta y = f(x_0 + Delta x) - f(x_0));如果 (Delta y) 与 (Delta x) 之比当 (Delta x o 0) 时的极限存在,那么称函数 (y = f(x)) 在点 (x_0) 处可导,并称这个极限为函数 (y = f(x)) 在点 (x_0) 处的导数,记为 (f'(x)) ,即
也可记作 (y'|_{x = x_0}),$$frac{dy}{dx}|_{x = x_0}$ 或 (frac{df(x)}{dx}|_{x=x_0})。
可以看出,导数等于 增量 (Delta y) 和增量 (Delta x) 比值的极限。
函数的微分
微分的定义: 设函数 (y=f(x)) 在某区间内有定义,(x_0) 及 (x_0 + Delta x) 在这个区间内,如果函数的增量
可表示为
其中,(A) 是不依赖于 (Delta x) 的常数,那么,称函数 (y=f(x)) 在点 (x_0) 是可微的,而 (ADelta x) 叫做函数 (y = f(x)) 在点 (x_0) 相应于自变量增量 (Delta x) 的微分,即
注: 函数 (f(x)) 在点 (x_0) 可微的充要条件是函数 (f(x)) 在点 (x_0) 可导。
微分的意思是指,因变量的增量 (Delta y),是自变量的增量 (Delta x) 的线性函数,且记作 (dy)。所以说,应该有如下关系:
增量 (Delta y) 是实实在在、真实的变化值。只是,只有当可导的时候,才能写成 (Delta y = A Delta x + mathit{o}(Delta x) = dy + mathit{o}(Delta x) = dy + mathit{o}(dy)) 。也就是说,微分,只是增量 (Delta y) 的一个近似值。
另外一点,在定义导数的时候,也是用增量 (Delta y) 与 (Delta x) 的比值来定义的,并不是用微分。只是,导数的值,刚好等于微分 (dy) 与 (dx) 的比值。
注二: 通常把自变量 (x) 的增量 (Delta x) 称为自变量的微分,记作 (dx),即 (dx = Delta x)。于是,函数 (y = f(x)) 的微分又可记作为
从而有
这就是说,函数的微分 (dy) 与自变量的微分 (dx) 之商等于该函数的导数,因此,导数也叫作“微商”。
微分的几何意义
如下图所示,自变量的增量为 (Delta x = PR) ,因变量的增量为 (Delta y = RQ) 。那么,在 (x_0) 点作曲线的切线,则得到函数 (y=f(x)) 在点 (x_0) 相应于自变量增量 (Delta x) 的微分 (dy = RQ') 。
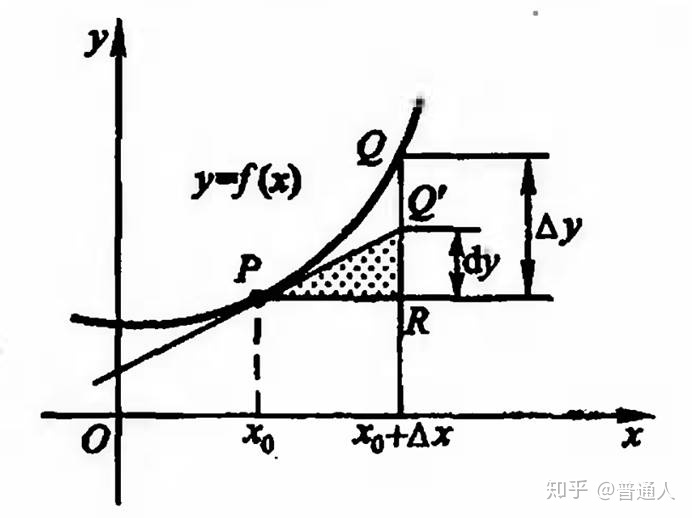
由此可见,对于可微函数 (y = f(x)) 而言,当 (Delta y) 是曲线 (y = f(x)) 上的点的纵坐标的增量时,(dy) 就是曲线的切线上点的纵坐标的相应增量。
只是,当 (|Delta x|) 很小时,$|Delta y - dy| 比 $|Delta x| 小得多。因此,在点 M 的邻近,我们可以用切线段来近似代替曲线段。在局部范围内用线性函数近似代替非线性函数,在几何上就是局部用切线段近似代替曲线段。这在数学上称为非线性函数的局部线性化,这是微分学的基本思想之一。
基本初等函数的微分公式与微分运算法则
从函数的微分表达式
可以看出,要计算函数的微分,只要计算函数的导数,再乘自变量的微分。那么,可得到如下的微分公式和微分运算法则:
(略)
偏导数
偏导数的定义: 设函数 (z=f(x,y)) 在点 ((x_0, y_0)) 的某一邻域内有定义,当 (y) 固定在 (y_0) 而 (x) 在 (x_0) 处有增量 (Delta x) 时,相应的函数有增量
如果
存在,那么称此极限为函数 (z = f(x, y)) 在点 ((x_0, y_0)) 处对 (x) 的偏导数,记作
如果函数 (z = f(x, y)) 在区域 (D) 内每一个点 ((x, y)) 处对 (x) 的偏导数都存在,那么这个偏导数就是 (x),(y) 的函数,它就称为函数 (z = f(x, y)) 对自变量 (x) 的偏导函数,记作
类似地,可以定义函数 (z=f(x,y)) 对自变量 (y) 的偏导函数,记作
注:偏导数仍然是增量的比值。
偏导数的几何意义:偏导数 (f_x(x, y)) 的几何意义是曲面被平面 (y = y_0) 所截得的曲线在点 (x_0) 处的斜率。
偏微分 / 全微分
根据一元函数微分学中增量与微分的关系,可得
上面两式的左端分别叫做二元函数对 (x) 和对 (y) 的偏增量,而右端分别叫做二元函数对 (x) 和对 (y) 的偏微分。
全增量: 设函数 (z = f(x,y)) 在点 (P(x, y)) 的某个邻域内有定义,(P'(x + Delta x, y+Delta y)) 为这个邻域内的任意一点,则称这两点的函数值之差 (f(x+Delta x, y+Delta y) - f(x,y)) 为函数在点 (P) 对应于自变量增量 (Delta x) 和 (Delta y) 的全增量,记作 (Delta z) ,即
注:一般来说,计算全增量 (Delta z) 比较复杂。与一元函数的情形类似,我们希望用自变量的增量 (Delta x) 和 (Delta y) 的线性函数来近似地代替函数的全增量 (Delta z),从而引入如下定义:
全微分的定义: 设函数 (z = f(x, y)) 在点 ((x, y)) 的某个邻域内有定义,如果函数在点 ((x, y)) 的全增量
可表示为
其中,(A) 和 (B) 不依赖于 (Delta x) 和 (Delta y) 而仅与 (x) 和 (y) 有关,( ho = sqrt{(Delta x)^2 +(Delta y)^2}),那么称函数 (z=f(x,y)) 在点 ((x,y)) 可微分,而 (ADelta x + BDelta y) 称为函数 (z=f(x,y)) 在点 ((x, y)) 的全微分,记作 (dz) ,即
可微与可导的关系
定理1: 如果函数 (z = f(x, y)) 在点 ((x, y)) 可微分,那么该函数在点 ((x, y)) 的偏导数 (frac{partial z}{partial x}) 与 (frac{partial z}{partial y}) 必定存在,且函数 (z = f(x, y)) 在点 ((x, y)) 的全微分为
定理2: 如果函数(z = f(x, y)) 的偏导数 (frac{partial z}{partial x}) 与 (frac{partial z}{partial y}) 在点 ((x, y)) 连续,那么该函数在该点可微分。
小结
总的来说,讲的是 增量、导数、微分 之间的关系。增量是变化的准确值,而微分,则是增量的一个近似值。导数,是该点处的斜率,也是增量比值的极限。