线段树

概述

      线段树是一种平衡二叉查找树，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。主要的处理思想是基于分治的思想。它的逻辑结构如下：线段树是一种平衡二叉查找树，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。主要的处理思想是基于分治的思想。它的逻辑结构如下：

    

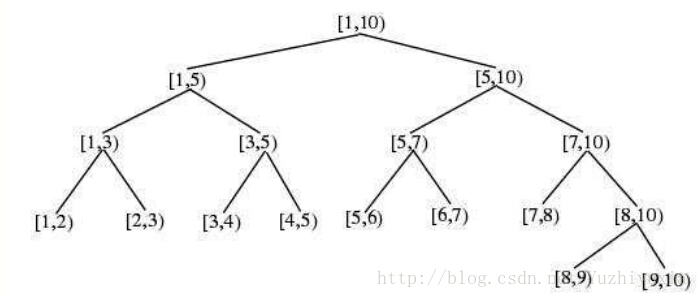
设根节点的区间为[a,b),区间长度为L = b - a，线段树的性质：

（1）线段树是一个平衡树，树的高度为log(L)

（2）线段树把区间上的任意长度为L的线段都分成不超过2log(L)线段的并

节点定义

 

 * public class SegmentTreeNode {
 *     public int start, end, max;
 *     public SegmentTreeNode left, right;
 *     public SegmentTreeNode(int start, int end, int max) {
 *         this.start = start;
 *         this.end = end;
 *         this.max = max
 *         this.left = this.right = null;
 *     }
 * }

 

建立

    public SegmentTreeNode buildTree(int start, int end, int[] A){
        if (start > end) return null;
        if (start == end){
            return new SegmentTreeNode(start, end, A[start]);
        }
        SegmentTreeNode node = new SegmentTreeNode(start, end, A[start]);
        int mid = (start + end) / 2;
        node.left = this.buildTree(start, mid, A);
        node.left = this.buildTree(mid + 1, end, A);
        if (node.left != null && node.left.max > node.max){
            node.max = node.left.max;
        }
        if (node.right != null && node.right.max > node.max){
            node.max = node.right.max;
        }
        return node;
    }

查询

    public int query(SegmentTreeNode root, int start, int end) {
        // write your code here
        if (root.start == start && root.end == end){
            return root.max;
        }
        int mid = (root.start + root.end) / 2;
        int leftM = Integer.MIN_VALUE, rightM = Integer.MIN_VALUE;
        if (start <= mid){
            if (mid < end){
                leftM =  query(root.left, start, mid);
            }else {
                leftM = query(root.left, start, end);
            }
        } 
        if (mid < end){
            if (start <= mid){
                rightM = query(root.right, mid + 1, end);
            }else{
                rightM = query(root.right, start, end);
            }
        }
        return Math.max(leftM, rightM);
    }

修改

    public void modify(SegmentTreeNode root, int index, int value) {
        // write your code here
        if (root.start == index && root.end == index){
            root.max = val;
        }
        int mid = (root.left + root.right) / 2;
        if (index >= root.start && index <= mid){
            modify(root.left, index, value);
        }
        if (index > mid && index < root.right){
            modify(root.right, index, value);
        }
        root.max = Math.max(root.left.max, root.right.max);
    }