配位堆模板

配位堆模板

复杂度：

• 合并(Merge): (O(1))
• 插入(Insert/Push): (O(1))
• 修改值(Change): (O(1)) or (O(logn))
• 取出维护的最值(Top): (O(1))
• 弹出堆顶元素(Pop): (O(logn))

这里特别说明一下，配位堆是支持单点修改的，只不过大根堆只能增值，小根堆只能减值，因为要维护堆的性质不变，复杂度(O(1))。想要修改成任意值也可以，可以先把要修改的点及其子树取出，并断开其与子树的连边，修改后再将 此点及其所有子树 与根合并，类似pop操作，复杂度大概是(O(logn))?,谨慎使用为好。

以大根堆为例

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#define N 10010
using namespace std;
template<class T,int maxsize,bool cmp(const T &a,const T &b)>
class Pairing_Heap
{
	private:
		T val[maxsize];
		int head[maxsize],next[maxsize],to[maxsize],fa[maxsize],root,size,cnt;
		int epool[maxsize],npool[maxsize],e,n;
		int stack[maxsize],t;
		inline int new_edge(){return e?epool[e--]:++cnt;}
		inline int new_node(){return n?npool[n--]:++size;}
		inline void add(int a,int b){int u=new_edge();to[u]=b;next[u]=head[a];head[a]=u;}
	public:
		Pairing_Heap(){e=n=size=cnt=root=t=0;}
		inline int merge(int a,int b){if(cmp(val[b],val[a]))swap(a,b);add(fa[b]=a,b);return a;}
		inline void push(T v){int u=new_node();val[u]=v;root=root?merge(root,u):u;}
		inline T top(){return val[root];}
		inline bool empty(){return !root;}
		inline void pop()
		{
			register int i;t=0;
			for(i=head[root];i;i=next[i]){epool[++e]=i;if(fa[to[i]]==root)fa[s[++t]=to[i]]=0;}
			fa[root]=head[root]=0,npool[++n]=root,root=i=0;
			while(i<t){++i;if(i==t){root=s[i];return;}int u=s[i],v=s[++i];s[++t]=merge(u,v);}
		}
}

Merge

直接根根合并，并使小根为大根子树（大根堆）

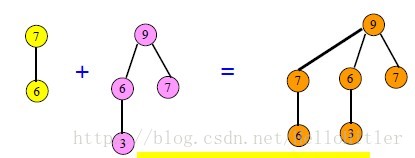
Push (Insert)

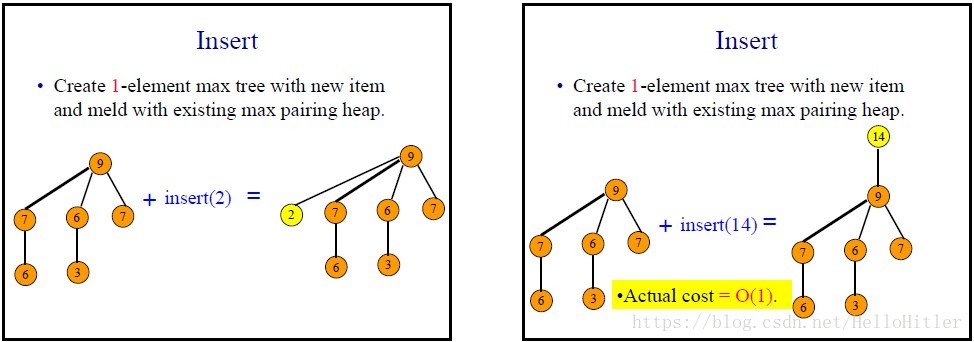
Modify

Pop