希尔排序比简单排序快得多,大约需要O(N×(logN)2)的时间,而且容易实现。希尔排序是基于插入排序,只是希尔排序不是比较相邻的数据,而是比较一定间隔的两个数据。
我们在选择排序算法时,基本上都可以使用希尔排序,如果有特殊要求或者算法不够快,在选择其他的排序算法。我们从插入排序的缺陷入手,看看问题:
问题:
插入排序思路:在标记符左边的数据是已经排序的,而右边的数据是没有排序,它有一个临时变量存储标记符所指的数据。当执行下一步是,从标记符数据项的左边第一个数据开始,依次次把左边的数据项与标记符所指的数据比较,直到找到临时变量所在的正确位置为止。
插入排序缺陷(即比较相邻数据的缺陷):当一个很小的数据在靠右的位置时,而这里应该是较大数据坐在的位置。要把值小的数据移动到左边,需要移动和比较的次数就会几乎等于N(假如有N个数据)。若数据量很大,则排序消耗的时间就会很长,效率几乎是O(N2)。
解决办法:
n-增量排序
1.通过加大排序中元素之间的间隔,在这些间隔的元素中进行插入排序。经过排序后,此时在n间隔的数据项已经是有序的。
2.减小排序间隔,在对这些间隔的数据项进行排序。重复执行,即依次减少间隔。
3.最后数据项间隔为1,即为插入排序。虽然此时的数据没有完全排好顺序,但是不会出现较小的数据在数据项左边的情形。
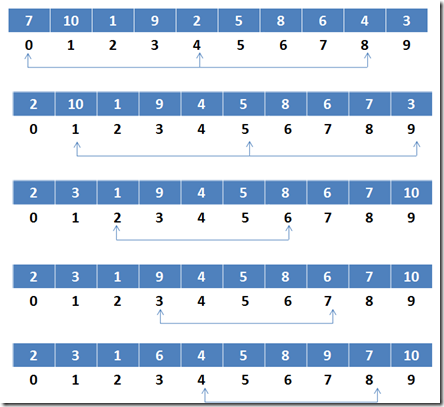
一.图说明:以n=3为间隔
经过4次排序后,可以看到数据的位置离正确的位置相差不远,此时在通过插入排序就能够快速的对整个数据项排列了。
二.间隔选择:
由于最后一次排序是插入排序,所以最后一次的间隔一定为1。我们反推回去,如果以3个间隔,则
1.倒数第二次的间隔为:1×3 + 1 = 4;
2.倒数第三次的间隔为:4×3 + 1= 13;
3.倒数第四次的间隔为:13×3 +1 = 40;
….
代码:
/** * 希尔排序实现 * * @param arr 数据项 */ public static void shellSort(int[] arr) { // 设置间隔初始值 int h = 1; // 这里取3作为间隔 while (h <= arr.length / 3) { h = h * 3 + 1; } while (h > 0) { for (int i = h; i < arr.length; i++) { // 存储当前比较的数据到临时变量,即相当于插入排序中的标识对应的数据 int temp = arr[i]; // 赋值给j,后面对j处理 int j = i; while (j > h - 1 && arr[j - h] >= temp) { // 移位,将小的arr[j - h]的数据移动到arr[j]的位置上 arr[j] = arr[j - h]; j = j - h; } // 将临时变量的数值赋值为arr[j],因为arr[j]的位置已经被arr[j - h]代替。 arr[j] = temp; } // 缩小h的范围 h = (h - 1) / 3; } }
代码单步调试过程中发现:for循环比较实际上数据比较顺序为(0,4),(1,5),(2,6),(3,7),(0,4,8),(1,5,9)。
总结:
希尔排序是非常实用的一种排序方法,在一般情况下使用希尔排序也能够满足大数据的要求(特殊场景除外),而且代码简单,效率比简单排序要好,是一个性价比很高的排序方法。