工作中总能遇到 一些 奇葩的需求,提出这些奇葩需求的人,多半也是奇葩的人,要么不懂相关的计算机软件知识,要么就是瞎扯蛋,异想天开,然而这些奇葩的需求,我也总能碰到。言规正传,在一次项目中,使用了 MindFusion 这个组件,在 Winform 窗体中画一些工序(生产中的工艺流程)节点,然后在工序节点间建立有向箭头连线,以此来表示工序的顺序,并行关系。因为有很多工序,每个工序都有一个持续时间,来表示该工序要多少时间才能完成,以天为单位,为了明确整个工序的工期,我们组的领导,想到用项目管理中的关键路径 (从工期开始到结束累计持续时间最长的一条或几条路径)来表示,这个倒是可以的,但是,项目中的每个工序的持续时间有问题,要么是0,要么是-1,要么是大于0的数字,这个就不能用关键路径的算法 来求了,而且工序的开始和结束 可以任意画,想画几个就画几个,想怎么连都可以,这也是个奇葩! 只能呵呵哒,领导还放话了,工序中持续时间为0或-1的可以忽略,这又是个奇葩,这样来看,是不能用关键路径 的算法 来求的,可领导的意图就是关键路径,还让求什么工序最晚开始时间,工序的松弛时间,这些完全是关键路径 中所用到的概念,必须得用关键路径 的算法, 因为工序中存在持续时间为0和-1的节点,用关键路径的算法来做,是行不通的!!! 我都怀疑领导是不是真的懂关键路径的一些概念,吧啦吧啦费了半天劲向领导解释关键路径的一些概念,他总算明白了点,最后决定只把耗时最长的一条或几条工序路径标记出来。这下好了,需求明确了,难度也不大,把图中从开始到结束间的所有可达路径遍历出来 ,然后找出累计持续时间最长一个或几个就行,解决方案如下 :
1. 考虑到 MindFusion 画的节点中,节点与节点间的关系,简单的表示如下 : A-->B A-->C B-->E C-->D D-->E,代码如下:
private void StuffLinks(DataRow[] rows) { foreach (DataRow dr in rows) { //这是业务逻辑,获取工序节点的名称 Model.DataSet_Config.PL_M_THRD_CFG_WORKRELATION2Row drRelation = dr as Model.DataSet_Config.PL_M_THRD_CFG_WORKRELATION2Row; // 连接名称 string linkName = drRelation.I_PREWORK_ID.ToString() + "-" + drRelation.I_SUBWORK_ID.ToString(); // hsLink 是哈稀表,用来保存工序节点间的连接, key: 连接名称 , value: 连接对象 if (!hsLink.Contains(linkName)) { // ShapeNode ,DiagramLink diagram 都是 MindFusion.Diagramming中的对象 // 前驱工序 ShapeNode preNode = (ShapeNode)hsNode[drRelation.I_PREWORK_ID]; // 后继工序 ShapeNode subNode = (ShapeNode)hsNode[drRelation.I_SUBWORK_ID]; // 工序间的连接 DiagramLink link = new DiagramLink(diagram, preNode, subNode); // 连接的画笔 link.Pen = _Pen; link.Tag = drRelation; link.AutoRoute = false; link.LayoutTraits[FlowLayoutTraits.LogicID] = "ControlFlow"; // 在图中添加连接,此时便会显示 diagram.Links.Add(link); // 向哈稀表中添加 link 对象 hsLink.Add(linkName, link); } } }
2. 要遍历这些工序节点间的路径,涉及到有向图路径的相关知识, 有向图中顶点的存储方式有两种: 一、用邻接表结构 ;二、用矩阵 ;用矩阵来存储,遍历比较复杂,也很消耗资源,在此采用了 邻接表结构,建立的邻接表结构如下 :
/// <summary> /// AOV 网邻接表数据结构 /// </summary> public class Vertex { /// <summary> /// 工序 /// </summary> public DiagramNode Node { get; set; } /// <summary> /// 前驱节点 /// </summary> public List<DiagramNode> PreNodes { get; set; } /// <summary> /// 后续节点 /// </summary> public DiagramNode DesNodes { get; set; } /// <summary> /// 工序的耗时 /// </summary> public decimal Weight { get; set; } /// <summary> /// 入度 /// </summary> public int InDegree { get; set; } /// <summary> /// 出度 /// </summary> public int OutDegree { get; set; } }
4. 通过工序节点来创建 AOV 网邻接表,为每一个节点设置入度和出度,用来区分是开始工序(只有出度没有入度)还是结束工序(只有入度没有出度),然后从结束节点开始向开始节点搜索(也可以从开始节点开始向结束节点搜索)具体代码如下:
/// <summary> /// 获取关键路径 /// </summary> private void GetCriticalPath() { // 原画笔颜色 var originalPenBrush = new MindFusion.Drawing.SolidBrush(Color.FromArgb(0, 0, 255)); // 原节点颜色 var originalNodeBrush = new MindFusion.Drawing.LinearGradientBrush(Color.FromArgb(255, 255, 0), Color.FromArgb(255, 255, 0), 30); for (int i = 0; i < stackCriticalPathLink.Count; i++) { DiagramLink item = stackCriticalPathLink.Pop(); item.Pen = this._Pen; item.Brush = originalPenBrush; item.HeadPen = this._Pen; } foreach (var v in listAllPath) { foreach (var item in v) { item.Node.Brush = originalNodeBrush; } } // 清空集合 listAllPath.Clear(); DiagramLinkCollection dlc = this.diagram.Links; if (dlc.Count == 0) { this.labelMsg.Text = "工序间未建立关系"; return; } // AOV 网节点 List<Vertex> listVertex = new List<Vertex>(); // 构造AOV 网数据结构 foreach (DiagramLink item in dlc) { var pre = item.Origin; var des = item.Destination; var vPre = listVertex.Find(p => p.Node.Equals(pre)); if (vPre == null) { vPre = new Vertex(); vPre.Node = pre; vPre.Weight = GetWeight((NodeTagAtrribute)pre.Tag); listVertex.Add(vPre); } var vDes = listVertex.Find(p => p.Node.Equals(des)); if (vDes == null) { vDes = new Vertex(); vDes.Node = des; vDes.Weight = GetWeight((NodeTagAtrribute)des.Tag); listVertex.Add(vDes); } } // 前驱工序,设置节点的出度,入度 foreach (var item in listVertex) { GetPreNodes(item, dlc); } // 终止节点,出度为0的节点 List<Vertex> listEnd = new List<Vertex>(); GetStartEndNodes(dlc, listVertex, listEnd); // 全部路径 GetAllPath(listVertex, listEnd); // 候选路径 List<decimal> listWeights = new List<decimal>(); foreach (var list in this.listAllPath) { decimal tempLength = list.Sum(p => p.Weight); listWeights.Add(tempLength); } // 关键路径 decimal pathLenth = listWeights.Max(); int num = 0; for (int i = 0; i < listWeights.Count; i++) { if (listWeights[i] == pathLenth) { var temp = listAllPath[num]; listAllPath[num] = listAllPath[i]; listAllPath[i] = temp; num++; } } int totalPath = this.listAllPath.Count(); // 移除不是关键路径的项 this.listAllPath.RemoveRange(num, listAllPath.Count() - num); // 关键路径节点,连线着色 Color lineColor = Color.FromArgb(255, 0, 0); Color nodeColor = Color.FromArgb(0, 255, 255); var penLine = new MindFusion.Drawing.Pen(lineColor, 1.0F); var penBrush = new MindFusion.Drawing.SolidBrush(lineColor); var nodeBrush = new MindFusion.Drawing.LinearGradientBrush(nodeColor, nodeColor, 30); // 关键路径中的节点着色 foreach (var item in listAllPath) { for (int i = 0, j = 0; i < item.Count; i++) { j = i + 1; var t = item[i]; if (j < item.Count) { var vertexDes = t.Node.Tag as NodeTagAtrribute; var vertexrPre = item[j].Node.Tag as NodeTagAtrribute; string key = vertexrPre._WorkOrder.I_ID.ToString() + "-" + vertexDes._WorkOrder.I_ID.ToString(); if (hsLink.Contains(key)) { DiagramLink link = hsLink[key] as DiagramLink; link.Pen = penLine; link.Brush = penBrush; link.HeadPen = penLine; stackCriticalPathLink.Push(link); } } t.Node.Brush = nodeBrush; } } if (totalPath > 0) { this.labelMsg.Text = string.Format("共 {0} 条路径,关键路径 {1} 条,长度:{2}(天)", totalPath, this.listAllPath.Count(), pathLenth); } else { this.labelMsg.Text = "工序间未建立关系"; } } /// <summary> /// 前驱节点,同时设置AOV 网节点的入度,出度 /// </summary> /// <param name="v"></param> /// <param name="dlc"></param> private void GetPreNodes(Vertex v, DiagramLinkCollection dlc) { v.PreNodes = new List<DiagramNode>(); foreach (DiagramLink item in dlc) { if (v.Node.Equals(item.Destination)) { v.PreNodes.Add(item.Origin); v.InDegree++; } if (v.Node.Equals(item.Origin)) v.OutDegree++; } } /// <summary> /// 获取起止节点 /// </summary> /// <param name="dlc"></param> /// <param name="listVertexs"></param> /// <param name="listEnds"></param> private void GetStartEndNodes(DiagramLinkCollection dlc, List<Vertex> listVertexs, List<Vertex> listEnds) { foreach (var item in listVertexs) { if (item.OutDegree == 0) listEnds.Add(item); } }
5. 节点路径 的搜索,这是本文要讲的关键,相关算法有:回溯法和非回溯法,具体代码如下:
/// <summary> /// 在AOV 网结构中, 从结束节点开始,倒序搜索从结束节点到开始节点,所有的可达路径 /// </summary> /// <param name="listVertex"></param> /// <param name="listEnd"></param> private void GetAllPath(List<Vertex> listVertex, List<Vertex> listEnd) { this.listAllPath.Clear(); this.stackRecallVertex.Clear(); for (int i = 0; i < listEnd.Count; i++) { List<Vertex> listResult = new List<Vertex>(); RecallSearchPath(listVertex, listEnd[i], listResult); //SearchPath(listVertex, listEnd[i]); } }
5.1 回溯法
/// <summary> /// 回溯搜索从结束节点到开始节点的所有可达路径 /// </summary> /// <param name="listVertex"></param> /// <param name="vertex"></param> /// <param name="listResult"></param> private void RecallSearchPath(List<Vertex> listVertex, Vertex vertex, List<Vertex> listResult) { List<DiagramNode> preNodes = vertex.PreNodes; listResult.Add(vertex); // 没有前驱节点,即到达开始节点 if (preNodes.Count == 0) { // 保存搜索的路径 listAllPath.Add(listResult); // 回溯前判断 if (this.stackRecallVertex.Count > 0) { // 从栈顶弹出一个回溯点,并进行回溯 var vPre = this.stackRecallVertex.Pop(); var vDes = listVertex.Find(p => p.Node.Equals(vPre.DesNodes)); int index = listResult.IndexOf(vDes); // 复制回溯点前的所有路径节点到新的集合 List<Vertex> listTemp = new List<Vertex>(); for (int i = 0; i <= index; i++) { listTemp.Add(listResult[i]); } RecallSearchPath(listVertex, vPre, listTemp); } } if (preNodes.Count > 1) { // 有大于一个分支,将所有分支压入回溯栈,并从栈顶弹出一个分支进行搜索 foreach (var item in preNodes) { var v = listVertex.Find(p => p.Node.Equals(item)); v.DesNodes = vertex.Node; this.stackRecallVertex.Push(v); } var vTop = this.stackRecallVertex.Pop(); RecallSearchPath(listVertex, vTop, listResult); } if (preNodes.Count == 1) { // 没有分支,直接进行搜索遍历,直到开始节点 var v = listVertex.Find(p => p.Node.Equals(preNodes[0])); RecallSearchPath(listVertex, v, listResult); } }
5.2 非回溯法
private void SearchPath(List<Vertex> listVertex, Vertex vertex) { // 栈,用于保存前驱顶点 Stack<Vertex> stackVer = new Stack<Vertex>(); // 保存一次完整搜索的顶点路径 List<Vertex> listResult = new List<Vertex>(); // 入栈 stackVer.Push(vertex); while (stackVer.Count > 0) { // 从栈顶弹出一个顶点,以此顶点,开始搜索 var vPre = stackVer.Pop(); List<DiagramNode> preNodes = vPre.PreNodes; listResult.Add(vPre); if (preNodes.Count >= 1) { // 前驱顶点有1个以上(即未到达开始顶点处),将所有前驱顶点压入栈 foreach (var item in preNodes) { var v = listVertex.Find(p => p.Node.Equals(item)); v.DesNodes = vPre.Node; stackVer.Push(v); } } else { // 没有前驱顶点,即搜索到达开始顶点处,将本次搜索的完整路径保存下来 // 保存搜索的路径 listAllPath.Add(listResult); // 判断栈内顶点数,若不为空, 获取栈的头部顶点的后继顶点的索引,并从索引0开复制到此索引处的顶点 if (stackVer.Count > 0) { var vDes = listVertex.Find(p => p.Node.Equals(stackVer.Peek().DesNodes)); int index = listResult.IndexOf(vDes); // 从索引0开复制到此索引处的顶点 List<Vertex> listTemp = new List<Vertex>(); for (int i = 0; i <= index; i++) { listTemp.Add(listResult[i]); } // 更新搜索路径中的顶点 listResult = listTemp; } } } }
6. 运行效果
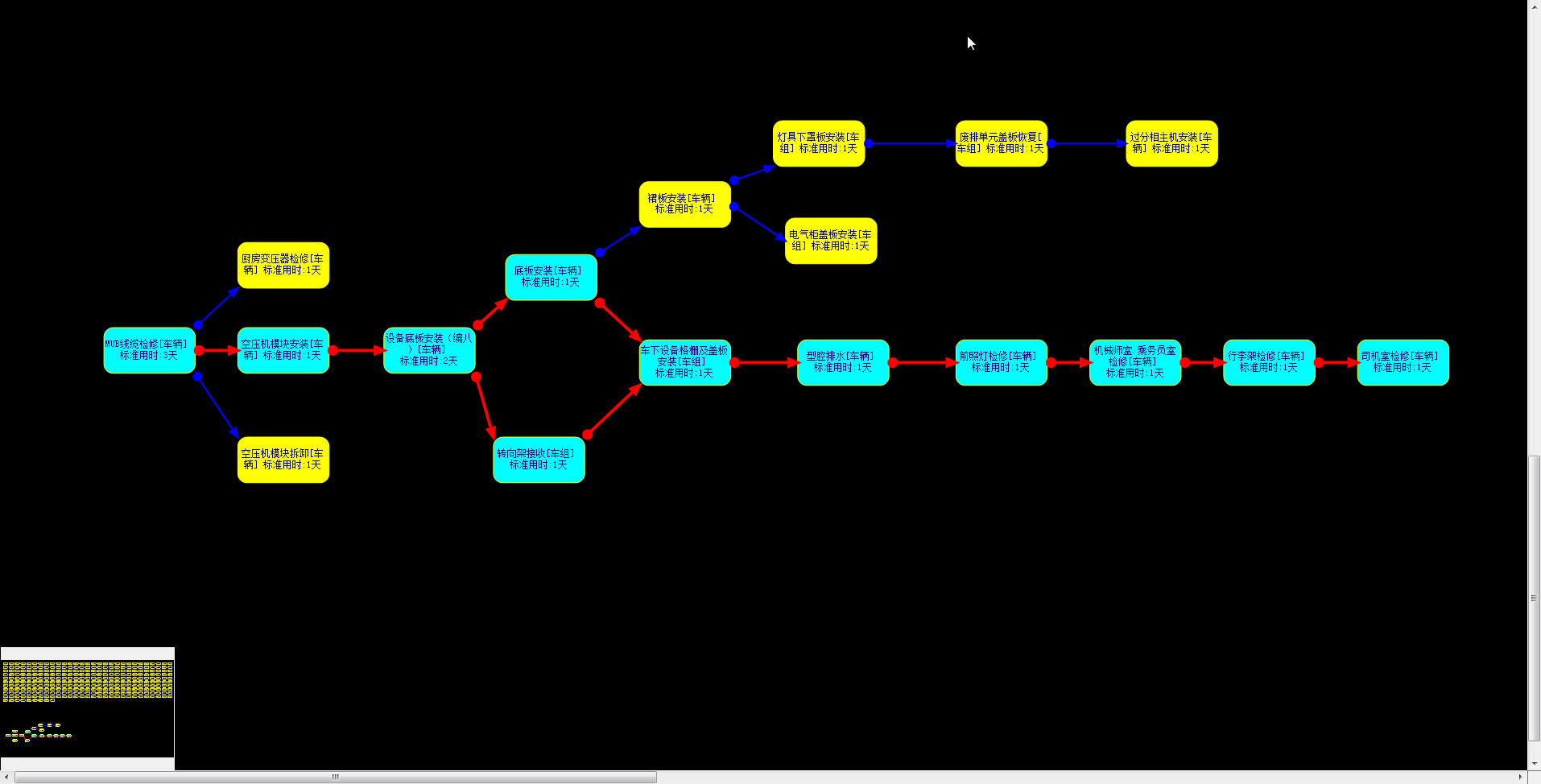
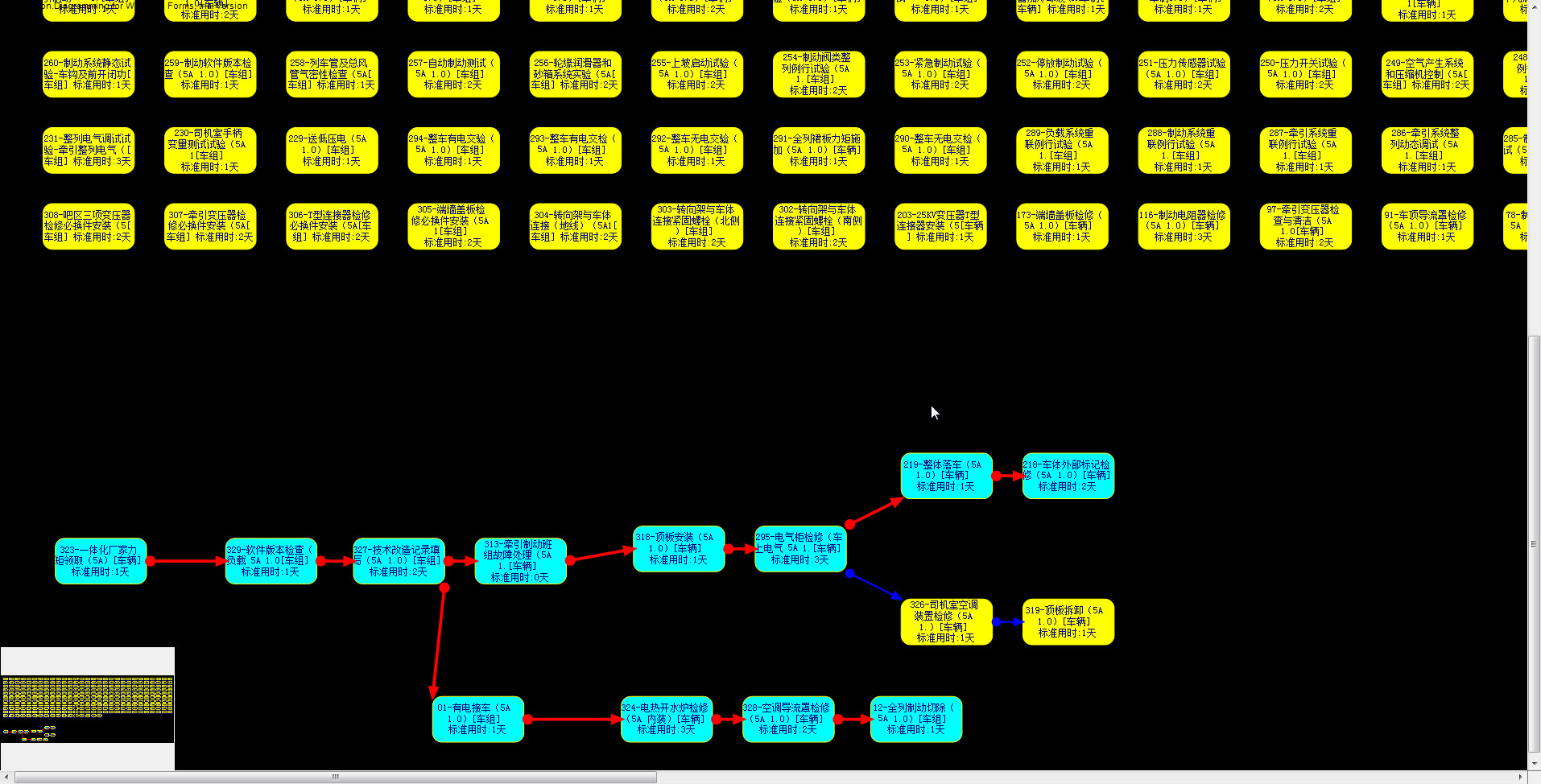
相关资料:
MindFusion官网组件:https://www.mindfusion.eu/winforms-ui-dock-control.html
MindFusion 官网API 文档:https://www.mindfusion.eu/onlinehelp/flowchartnet/index.htm
关键路径算法:https://www.jianshu.com/p/1857ed4d8128
回溯算法:https://zh.wikipedia.org/wiki/%E5%9B%9E%E6%BA%AF%E6%B3%95