SIGAI机器学习第七集 k近邻算法

讲授K近邻思想，kNN的预测算法，距离函数，距离度量学习，kNN算法的实际应用。

KNN是有监督机器学习算法，K-means是一个聚类算法，都依赖于距离函数。没有训练过程，只有预测过程。

大纲：

k近邻思想
预测算法
距离函数
距离度量学习
实验环节
实际应用

k近邻思想：

KNN基于模板匹配的思想，如要确定一个水果的类别，可以拿各种水果出来，看它和哪种水果长得像，就判定为哪种水果，这就是模板匹配思想。要拿一些实际的例子来，这些例子就相当于一些标准的模板，要预测样本属于哪个类型，就和这些例子比一遍，看和哪个长得最像就归到哪个类。

预测算法：

KNN算法是没有训练过程的，无train这个函数的，分类或者回归的时候现算，拿待预测样本和每个样本比较一下找到和它最像的K个样本再来投票，K一般凭经验来设置，二分类问题要设置为奇数（偶数在投票时可能两个类票数相等），既可用于分类问题也可用于回归问题。

分类问题
1.计算邻居节点
2.投票
回归问题
1.计算邻居节点
2.计算均值

距离函数：

KNN依赖于一个距离函数（或相似度函数，距离越近相似度越大）。

距离函数将两个样本对应的特征向量映射为大于等于0实数，距离函数要满足：

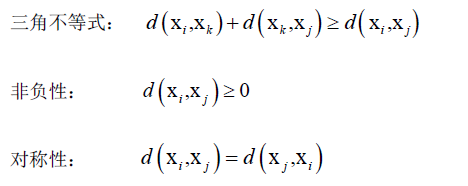
 只要满足上面三条的函数都可以拿来做距离函数。几种常见的距离：

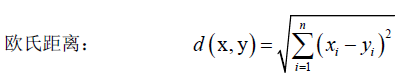
 马氏距离，里边是一个二次型，显然这个二次型要半正定才可以（不然开根号没意义），即矩阵S半正定，S可以有很多种讲究，如协方差矩阵，一般取成对称的正定矩阵，S可以通过度量学习学习到。这种距离是一种概率意义上的距离，欧氏距离不考虑样本的分布，而马氏距离考虑样本的分布，如两类样本服从同一分部的话还考虑它的方差，相当于对方差做了一个归一化一样。

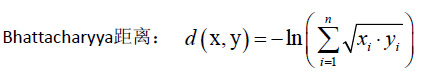巴氏距离，用于直方图这样的特征，x满足∑x_i=1且x_i≥0，y_i也是如此。

 距离度量学习：

如马氏距离中的矩阵S的通过学习得到，这就叫做距离度量学习，即通过训练样本学习一种距离函数。

Kilian Q Weinberger, Lawrence K Saul. Distance Metric Learning for Large Margin Nearest Neighbor Classification. 2009, Journal of Machine Learning Research.

这篇论文是用于KNN的距离度量学习，保证对样本进行变换之后，同类样本是k个最近的邻居，不同的样本尽可能远离本样本。

将样本x通过一种线性变换，左乘一个矩阵L（L是通过学习得到的），得到一个向量y，就变换到另外一个空间中去了，变换完之后要保证变换完的每一个样本它和离他最近的k个邻居都和他是同一个类，而和它不同的类的样本离他尽可能的远，也就是说和他同类的样本尽量拉到它的k个邻居里边去，而和他不同类的样本把它推开。

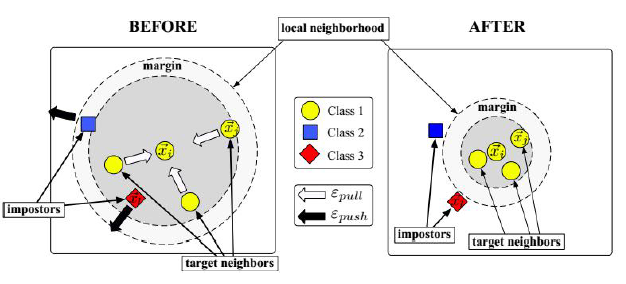
算法原理：

目标邻居：j~->i，指j和i是同一类且在i的k个邻居里边，这种叫目标邻居，变换的目标是让目标邻居真正成为它的k个邻居之一。

冒充者：，变换完之后，任意一个样本l他和i的距离小于等于i和j的距离加1，j和i是同一种类型，j本来该属于i的最近的k个邻居之一的，冒充者它和i的距离很接近了，比j和i的距离远不了多少，冒充者试图想冲到i的k个邻居里边去，冒充i的真正的邻居，但实际上他们是不同类型的。那么算法就有了优化的目标，通过一种变换L，把原始样本变换到新的空间里边去，保证所有目标邻居尽量是k个邻居，不是同一类的样本尽量推开，间隔至少为1，建立一个间隔。

优化目标函数：（分拉函数和推函数）

把和x_i相同类型的样本x_j拉到最近的k个邻居里来，距离尽可能的接近。

 拉损失函数：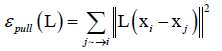

 推损失函数：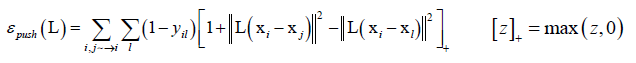

 推损失函数只对不同类型的样本起作用，y_i、y_l不同类y_il=0，否则y_il=1。

总损失函数：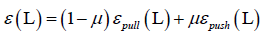

 目标是最小化拉函数、推函数，即最小化总损失函数，μ是人工设定的参数，用来平衡拉和推之间的作用，求解这样一个最优化问题，最终得到线性变换的矩阵L。对所有样本先用L变换一遍，再算它们之间的距离。

 ||L(X-Y)||²=(L(X-Y))^TL(X-Y)=(X-Y)^TL^TL(X-Y)，这里的L^TL就是我们要学习的马氏距离中的矩阵S，本质上就学到了这么一种变换矩阵的距离定义，在这种距离定义下是最利于KNN的分类算法的，把同类的样本尽可能的拉成k个邻居，然后不同类的样本尽可能的分开。通过这么一种简单的变换可以显著的提高KNN算法的精度。

距离度量学习是一种通用的机器学习算法，它的核心思想是根据一组样本（(x₁,y₁),(x₂,y₂),...）学习一种度量函数（距离函数）出来，然后达到某种目标，如让同类样本尽可能的进不同类样本尽可能远，除了这种定义外还有其他的一些构造的技巧，来达成不同的目的的。把同类样本拉到一起不同样本推开的这种思想在机器学习里边是非常常见的对于分类问题，后边的线性判别分析LDA、深度学习里边的某些算法如人脸识别里边的损失函数，都是一样的思想。

实验环节：

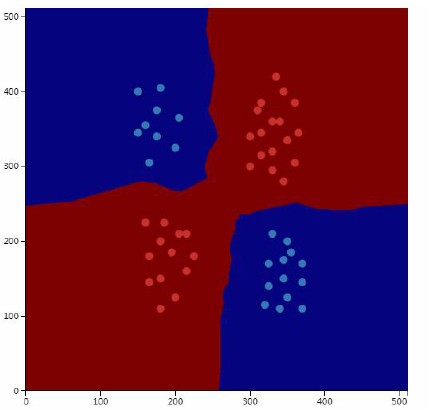
KNN算法是一种判别模型，非线性模型，既可用于分类问题也可用于回归问题，并且它还支持多分类，因此它是一种简单但是很有效的机器学习算法。

贝叶斯分类器是一种生成模型，因为它对联合概率概率密度函数进行建模了，对p(x|y)进行建模的，它只是用来做分类的一种算法，而且是一种非线性的模型，可以解决异或模型，支持多分类。

决策树是一种判别模型，它也是一种非线性模型，支持多分类，决策树既可以用于分类问题也可以用于回归问题。

KNN没有训练过程，只能预测。

实际应用：

实现简单
向量维数高，训练样本数大的时候，计算量大，计算出到所有样本的距离之后，找出topk个样本，找topk也有相应的经典算法。
文本分类
图像分类，如人脸识别，通过机器学习对每个人脸找到一个特征向量，然后用KNN进行分类。

最小距离分类器是KNN的特殊情况，k为1时候的情况，也叫最近邻分类器。

本集总结：

KNN依赖于特征向量x提的好不好，如果特征向量本身有区分度的话，KNN算法的性能是非常好的。