SIGAI机器学习第十五集 支持向量机2

讲授线性分类器，分类间隔，线性可分的支持向量机原问题与对偶问题，线性不可分的支持向量机原问题与对偶问题，核映射与核函数，多分类问题，libsvm的使用，实际应用

大纲：

SVM求解面临的问题

SMO算法简介

子问题的求解

子问题是凸优化的证明

收敛性保证

优化变量的选择

完整的算法

SVM求解面临的问题：

SVM的对偶问题是求解一个二次函数的极值问题（二次规划问题）：

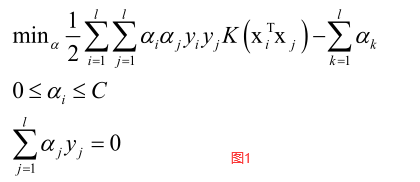
 前边一项是二次型，带有不等式约束和等式约束，C是惩罚因子。

写成矩阵形式：

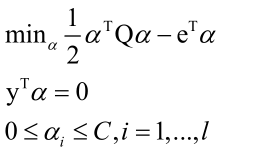
 二次规划问题可以用梯度下降法、牛顿法、坐标下降法等等进行求解，但是它们都会面临问题。计算效率问题：Q矩阵是l×l，其中l是样本数目，如果样本很多的话算起来效率会非常低；存储空间问题：Q矩阵太大，如一百万样本占用内存1M*1M*每个数据占的字节数，会占用大量的存储空间，非常占内存；带有不等式和等式约束约束，用梯度下降法或牛顿法求解时同时满足等式约束，求解起来很不方便。所以要找其他算法能更高效的求解问题，SMO算法就诞生了。

SMO算法简介：

Sequential minimal optimization，顺序最小优化。Platt等人于1998年提出，SVM时1995年提出，三年内一直没找到高效的训练算法，直到SMO算法出现，SVM才大规模的普及，之后采用非线性核的SVM都用SMO算法来训练。

核心思想是分治法，每次挑选出两个变量进行优化，因为由等式约束y^Tα=0，所以要改变α中一个变量则会破坏等式约束，所以每次要挑选α中两个变量进行优化才能满足等式约束。

定义以下变量：

u_i相当于预测方程，如果把x_i看成x，就相当于f(x)预测方程，拿x和所有y做映射然后和标签值相乘再求和再加b。

利用KKT条件作用于原问题，可得出三种情况（见上节课）：

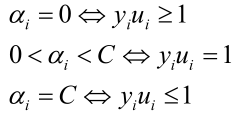
a_i=0时相当于将样本带入预测函数u_i和标签值相乘大于等于1。其他情况同理。后边会根据这个选择优化变量α_i、α_j。

子问题的求解：

怎么来求解两个变量的子问题？

挑两个变量α_i、α_j，怎么挑的这里先不讨论，图1中只有一部分是和α_i、α_j有关的，其它的变量都视为常数只考虑α_i、α_j，展开得到：

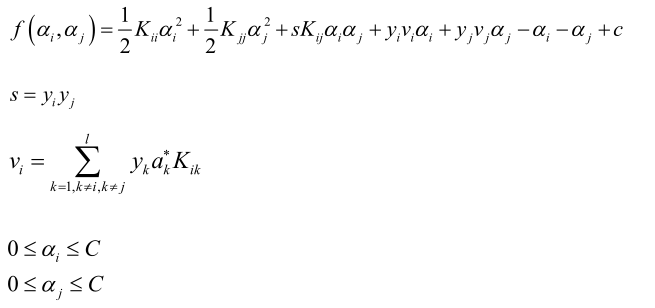
展开成只管α_i、α_j的一个二次函数。由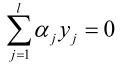得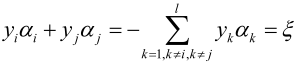，，即yi和yj是满足一个线性约束关系，yi、yj可以用一个表示另一个，则f(ai,aj)就变成一个带有不等式约束的一元二次函数在某个区间的极值问题。

 其中yi、yj可能同号或异号：

 在得到αj的范围之后，就是求f(αj)的一元二次方程的极值问题，有三种情况：

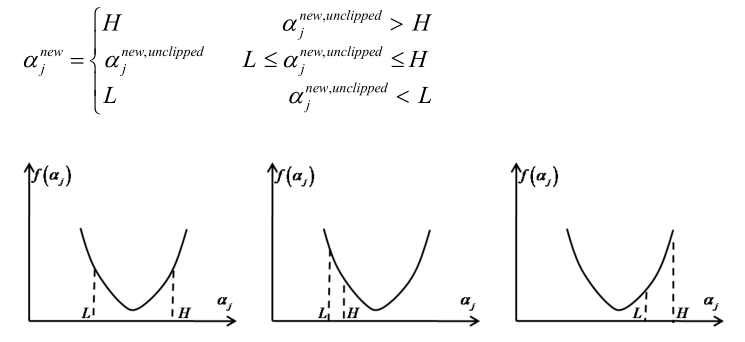
 分三种情况就可以把一元二次函数极值求出来了，现在不考虑分三种情况来求解极值：

 则可以求解出极值点aj的值，也可以求得ai的值：

 ai、aj求得的是精确解公式解。

 子问题是凸优化的证明：

是否能保证上边的一元二次函数抛物线开口向上？答案是可以的。

整个对偶问题是凸优化问题，随意挑出俩个变量ai、aj后形成的问题仍然是凸优化问题：

二元二次函数f(ai, aj)的Hession矩阵为：

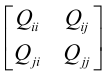， 其中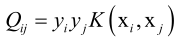，Hession矩阵相当于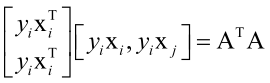，不过这里没有用核函数，可知Hession矩阵大于等于0，半正定，如果等于0相当于一次函数，可以用技巧把它规避掉。

所以对于支持向量机，无论是它的对偶问题，还是子问题，都是一个凸优化问题，因此一定可以找到它的一个全局极小值点。

 收敛性保证：

无论本次迭代时两个变量的初始值是多少，通过上面的子问题求解算法得到是在可行域里的最小值，因此每次求解更新这两个变量的值之后，都能保证目标函数值小于或者等于初始值，即函数值下降，所以SMO算法能保证收敛。
优化变量的选择：

优化变量ai、aj怎么选择呢，在最优点处ai、aj必须满足KKT条件，也就是说，如果ai、aj不满足KKT条件，也就是还没到达全局极小值点处，因此就把违反KKT条件的变量挑出来，然后不断调整变量让它往满足KKT条件方向调整，最后才能收敛到全局极小值处。

 依次选择ai的三个区间，找到不满足KKT条件的ai去优化它，如果三个区间都找不到，说明算法已经收敛了。

ai找到之后，再找aj，启发式搜索，相当于贪心算法，找到最优的aj，，使得调整值Ei最大，那样函数值才下降的最快，即找使得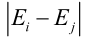最大的aj，这样就把ai、aj找出来了，当然还有其他算法找ai、aj。

 完整的算法：

 实现细节问题：

初始值的设定，一般设置为全0向量，因为α要满足约束条件（y^Tα=0，0≤ai≤C），所以另ai初值为0满足约束条件。

迭代终止的判定规则，如果找不到ai、aj使得满足KKT条件，那么算法收敛终止，然后设置一个阈值达到一定的迭代次数算法终止。