冒泡排序
冒泡排序是最简单的排序算法,它通过重复交换相邻元素(如果它们的顺序不正确)来工作。
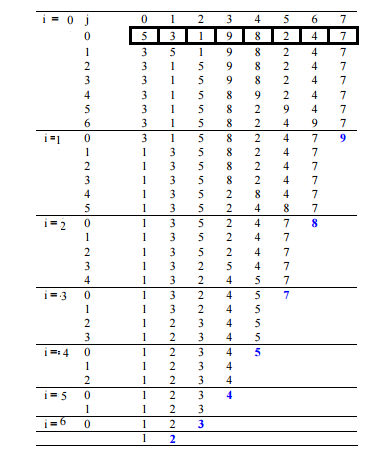
例如:
第一遍:
(5 1 4 2 8)->(1 5 4 2 8),这里,算法比较前两个元素,由于5>1所以交换。
(1 5 4 2 8)->(1 4 5 2 8),交换,由于5>4。
(1 4 5 2 8)->(1 4 2 5 8),交换,由于5>2。
(1 4 2 5 8)->(1 4 2 5 8),现在,由于这5,8元素已经是有序的(8>5),算法不交换它们。
第二遍:
(1 4 2 5 8)->(1 4 2 5 8)。
(1 4 2 5 8)->(1 2 4 5 8),交换由于4>2。
(1 2 4 5 8)->(1 2 4 5 8)。
(1 2 4 5 8)->(1 2 4 5 8)。
现在,数组已经排序,但我们的算法不知道它是否完成。该算法需要一整遍而没有任何交换才能知道它已排序。
第三遍:
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
下面是气泡排序的实现。
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <stdbool.h>
int *getRandArray(int max, int min, int n)
{
srand(time(NULL));
int *array = (int *)malloc(sizeof(int) * n);
for(int i=0; i<n; i++)
array[i] = rand() % max + min;
return array;
}
void printArray(int *array, int n)
{
for(int i=0; i<n; i++)
printf("%d ", array[i]);
printf("
");
}
void swap(int *xp, int *yp)
{
int temp = *xp;
*xp = *yp;
*yp = temp;
}
void bubbleSort(int arr[], int n)
{
int i, j;
// 进行n-1次遍历
for(i=0; i<n-1; i++) {
// 每次遍历最后一个元素已经归位
for(j=0; j<n-1-i; j++) {
if(arr[j] > arr[j+1])
swap(&arr[j], &arr[j+1]);
}
// n-1 次遍历后,n-1个元素都归位,最后一个默认归位,排序完毕
}
}
int main()
{
int len = 30;
int *arr = getRandArray(100, 1, len);
printArray(arr, len);
// 排序
bubbleSort(arr, len);
printArray(arr, len);
free(arr);
return 0;
}
图例
优化措施:
上述函数始终运行(O(n^2))次,即使数组已排序。如果内部循环没有导致任何交换,可以通过停止算法来优化它。
代码实现
// 冒泡排序的优化版本
void bubbleSort(int arr[], int n)
{
int i, j;
bool swapped;
for (i = 0; i < n-1; i++)
{
swapped = false;
for (j = 0; j < n-i-1; j++)
{
if (arr[j] > arr[j+1])
{
swap(&arr[j], &arr[j+1]);
swapped = true;
}
}
// 如果内部循环没有交换两个元素,则退出循环
if (swapped == false)
break;
}
}
简洁版本
void bsort(int arr[], int n)
{
int sorted = 0, tmp;
for( ; !sorted; n--) {
sorted = 1;
for(int i=1; i<n; i++) {
if(arr[i] < arr[i-1]) {
tmp = arr[i];
arr[i] = arr[i-1];
arr[i-1] = tmp;
sorted = 0;
}
}
}
}
最差和平均情况时间复杂度:O(n*n)。最坏的情况发生在对数组进行反向排序时。
最佳情况时间复杂度:O(N)。最好的情况发生在数组已经排序时。
辅助空间:O(1)。
边界情况:当元素已经排序时,冒泡排序需要最少的时间(n阶数)。
就地排序:是。
稳定:是。
由于它的简单性,冒泡排序经常被用来引入排序算法的概念。
在计算机图形学中,其检测几乎排序的阵列中的非常小的错误(如仅两个元素的交换)并仅以线性复杂度(2n)修复它的能力是很受欢迎的。例如,它用于多边形填充算法,其中边界线按其在特定扫描线(平行于x轴的线)处的x坐标排序,并且随着y递增,其顺序变化(两个元素被交换)仅在两条线的相交处(来源:Wikipedia)