LeetCode 72. 编辑距离

72. 编辑距离

难度困难

给你两个单词 word1 和 word2，请你计算出将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

1. 插入一个字符
2. 删除一个字符
3. 替换一个字符

示例 1：

输入：word1 = "horse", word2 = "ros"
输出：3
解释：
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')

示例 2：

输入：word1 = "intention", word2 = "execution"
输出：5
解释：
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')

思路：小生不才，这道题想了半天，没有找到解决办法，所以参考了题解。

动态规划：
dp[i][j] 代表 word1 到 i 位置转换成 word2 到 j 位置需要最少步数

所以，

　　当 word1[i] == word2[j]，dp[i][j] = dp[i-1][j-1]；

　　当 word1[i] != word2[j]，dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1

其中，dp[i-1][j-1] 表示替换操作，dp[i-1][j] 表示删除操作，dp[i][j-1] 表示插入操作。

注意，针对第一行，第一列要单独考虑，我们引入 '' 下图所示：

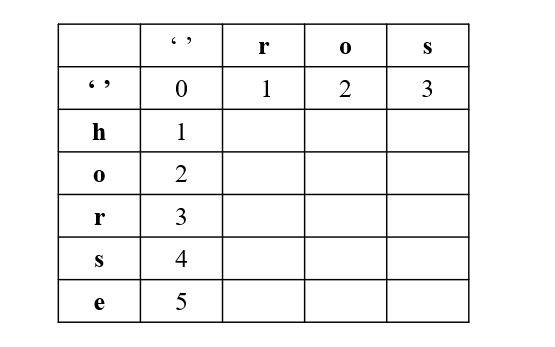
　　第一行，是 word1 为空变成 word2 最少步数，就是插入操作

　　第一列，是 word2 为空，需要的最少步数，就是删除操作

代码如下：

int min(int a,int b,int c)
{
    int d=a<b?a:b;
    return d<c?d:c;
}

int minDistance(char * word1, char * word2){
    int i,j;
    int len1=strlen(word1);
    int len2=strlen(word2);
    // 每个结点为一维数组的顺序表
    int** dp=(int**)malloc((len1+1)*sizeof(int*));
    for(i=0;i<=len1;i++)
    {
        dp[i]=(int*)malloc((len2+1)*sizeof(int));
    }

    // 初始条件、边界条件
    for(i=0;i<=len1;i++)  
    {
        dp[i][0]=i;
    }
    for(j=0;j<=len2;j++)
    {
        dp[0][j]=j;
    }

    // 状态转移方程
    for(i=1;i<=len1;i++)
    {
        for(j=1;j<=len2;j++)
        {
            if(word1[i-1]==word2[j-1])
            {
                dp[i][j] = dp[i-1][j-1];
            }else{
                dp[i][j]=1+min(dp[i][j-1],dp[i-1][j],dp[i-1][j-1]);
            }
        }
    }

    return dp[len1][len2];
}