A. Two Rabbits【思维】

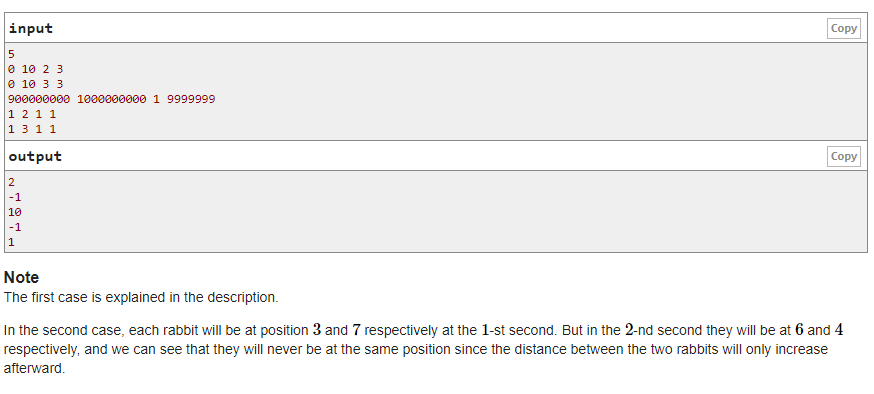
题意:两只兔子同时往中间有规律地跳,问是否可以同时跳到同一点
题解:算一下距离是否是每回合缩短距离的倍数即可
#include<iostream> #include<cstdio> #include<cstdlib> #include<algorithm> #include<cmath> #include<cstring> #include<string> #include<vector> #include<queue> #include<stack> #define ll long long using namespace std; int T; ll x,y,a,b; int main() { scanf("%d",&T); while(T--) { scanf("%lld%lld%lld%lld",&x,&y,&a,&b); ll ans=(y-x)/(a+b); if((y-x)%(a+b)==0)printf("%lld ",ans); else printf("-1 "); } return 0; }
B. Longest Palindrome【回文】
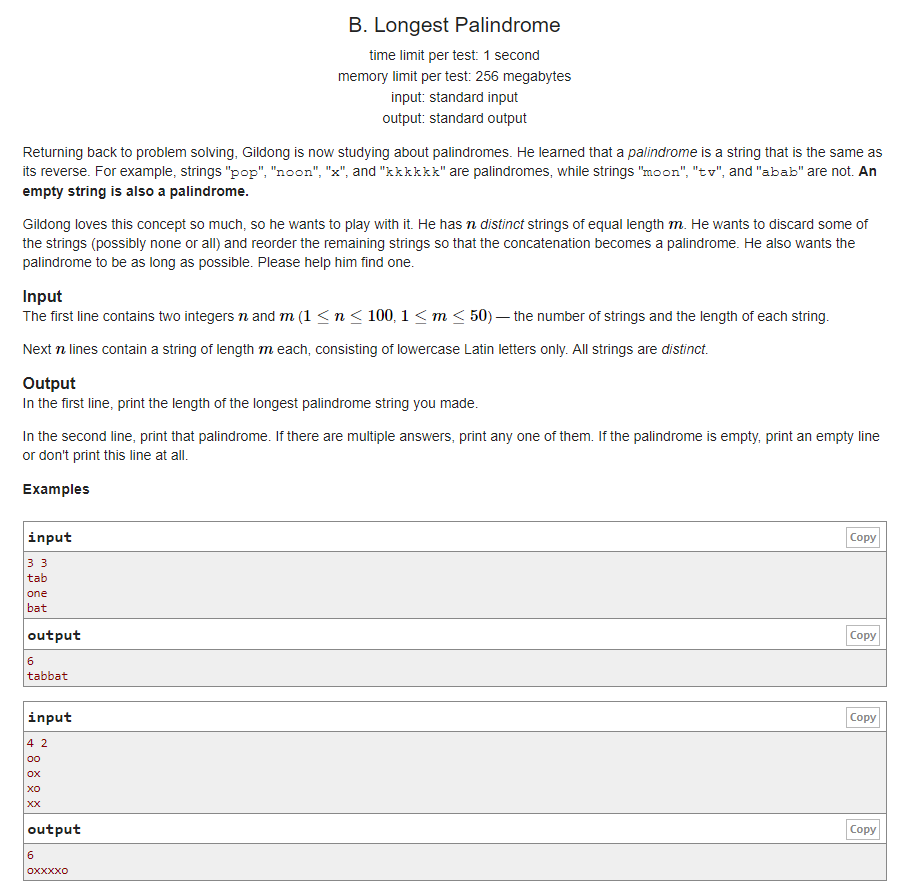
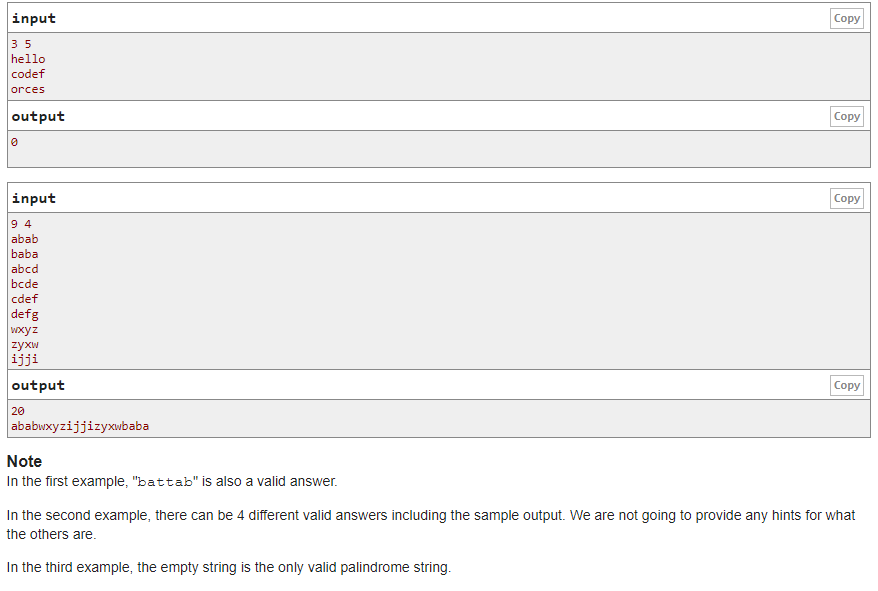
题意:给你n个串,让你重新选择若干个串并排序成一个新串,使得新串是回文串
题解:判断每一个串可以和哪个串形成回文,这样属于一对,最大匹配可以直接贪心求,注意中间部分可以放一个自己跟自己回文的单独串
#include<iostream> #include<cstdio> #include<cstdlib> #include<algorithm> #include<cmath> #include<cstring> #include<string> #include<vector> #include<queue> #include<stack> #define ll long long using namespace std; int n,l; char ch[101][51]; int fl[101][101]; bool check(int x,int y) { for(int i=0;i<l;i++)if(ch[x][i]!=ch[y][l-i-1])return 0; return 1; } char ansch[1000001]; int anschi,fl2[101]; int main() { scanf("%d%d",&n,&l); for(int i=1;i<=n;i++)scanf("%s",ch[i]); for(int i=1;i<=n;i++) for(int j=i;j<=n;j++) if(check(i,j))fl[i][j]=fl[j][i]=1; int ans=0; for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) if(i!=j && fl[i][j]==1 && fl2[i]==0 && fl2[j]==0) { ans+=2; for(int k=0;k<l;k++)ansch[anschi++]=ch[i][k]; fl2[i]=fl2[j]=1; } ans*=l; int t=anschi-1; for(int i=1;i<=n;i++) if(fl2[i]==0 && fl[i][i]==1) { ans+=l; for(int j=0;j<l;j++)ansch[anschi++]=ch[i][j]; break; } for(int i=t;i>=0;i--)ansch[anschi++]=ansch[i]; printf("%d %s ",ans,ansch); return 0; }
C. Air Conditioner【思维】

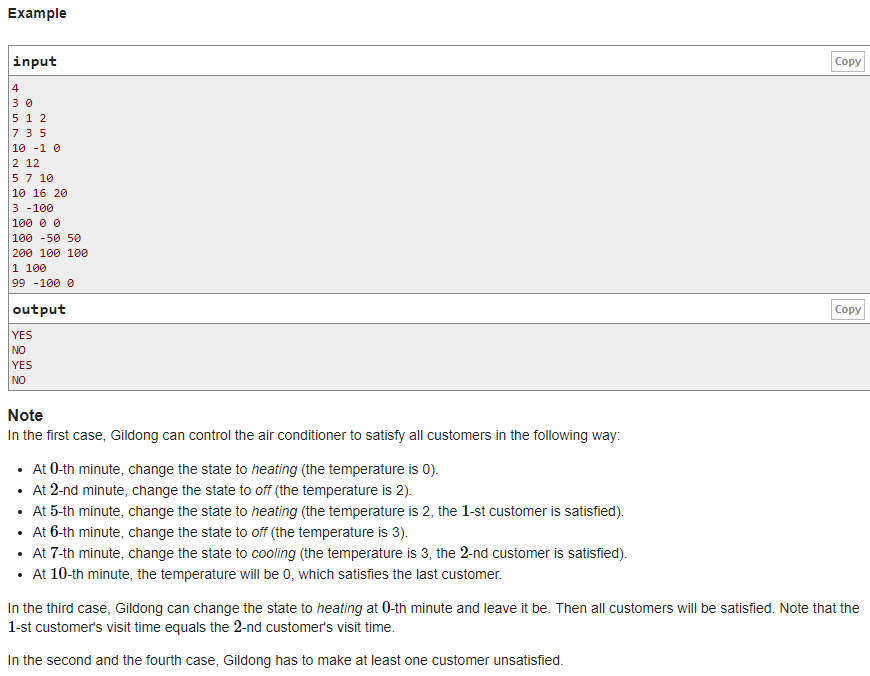
题意:开始时刻为0,处于位置s,现有m个需求,每个需求为ti时刻需要在[li,ri]位置,每个时刻只能朝相邻一格方向行走,问是否存在行走方案满足所有需求
题解:保证需求时刻从小到大排序,那么我们可以求一个i需求到i+1需求中存在行走方案到达点的范围,这样只需要判断是否存在交集即可
#include<iostream> #include<cstdio> #include<cstdlib> #include<algorithm> #include<cmath> #include<cstring> #include<string> #include<vector> #include<queue> #include<stack> #define ll long long using namespace std; int T; int n,s; struct node { int t,x,y; }r[101]; int main() { scanf("%d",&T); while(T--) { scanf("%d%d",&n,&s); for(int i=1;i<=n;i++)scanf("%d%d%d",&r[i].t,&r[i].x,&r[i].y); ll nowt=0,lt=s,rt=s,fl=0; for(int i=1;i<=n;i++) { lt-=r[i].t-nowt;rt+=r[i].t-nowt; if(rt<r[i].x || lt>r[i].y){fl=1;break;} lt=max(lt,(ll)r[i].x);rt=min(rt,(ll)r[i].y); nowt=r[i].t; } printf(fl?"NO ":"YES "); } return 0; }
D. Shortest and Longest LIS【构造】
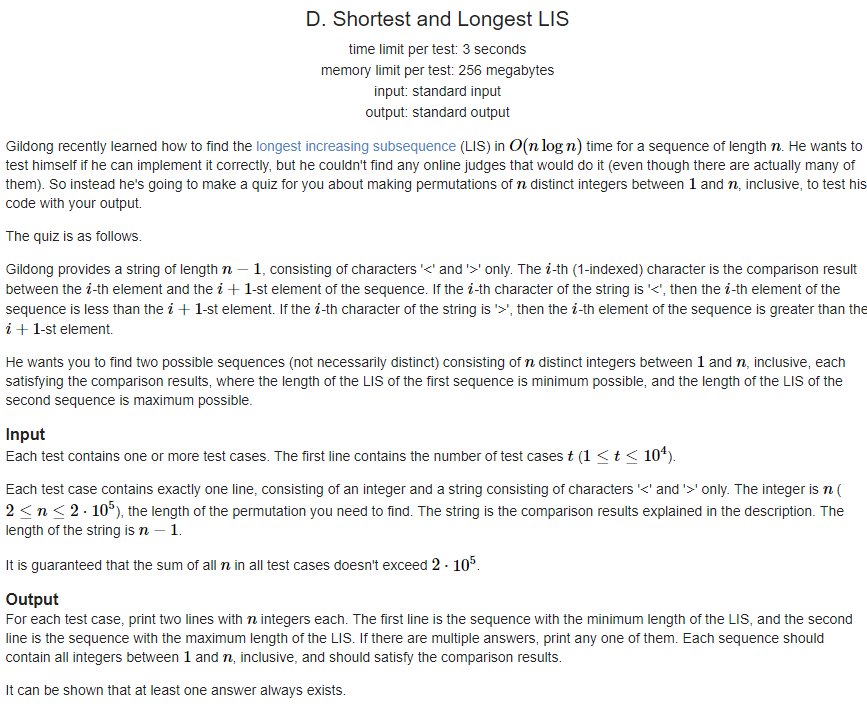
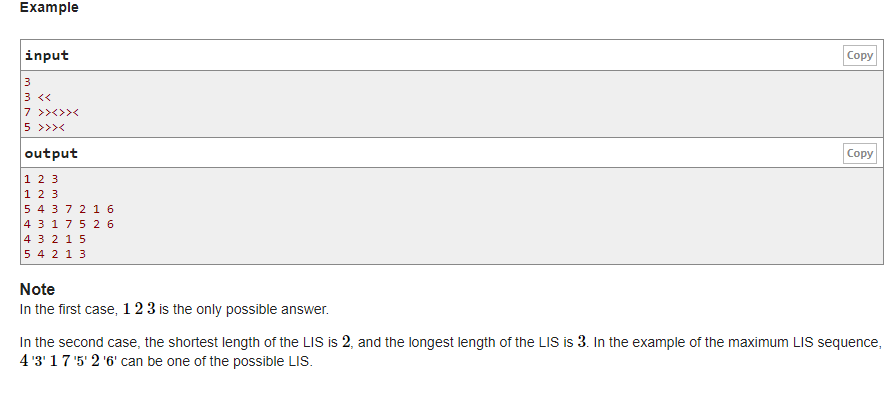
题意:给定长度为n的排列相邻数之间的大小关系,让你构造满足其大小关系的最长LIS和最短LIS的排列
题解:最长LIS:显然为<的个数+1,那么对于每个<,只需要在大的数放最大的数即可,那么从后往前找<,找到一个放一个当前还未使用的最大的数
最短LIS:显然为最长的连续<的连续数+1,那么对于每个连续的<,只需要连着放最小的数即可,那么从后往前找<,找到一组连续的就连着放还未使用的最小的数
#include<iostream> #include<cstdio> #include<cstdlib> #include<algorithm> #include<cmath> #include<cstring> #include<string> #include<vector> #include<queue> #include<stack> #define ll long long using namespace std; int T,n; char ch[200001]; int mx[200001],mn[200001]; int main() { scanf("%d",&T); while(T--) { scanf("%d%s",&n,ch); int t=n; for(int i=n-2;i>=0;i--)if(ch[i]=='<')mx[i+2]=t--; for(int i=1;i<=n;i++)if(!mx[i])mx[i]=t--; t=1; int fl=0; for(int i=n-2;i>=0;i--) { if(ch[i]=='<') { int j; for(j=i-1;j>=0;j--)if(ch[j]!='<')break; if(ch[j]!='<')j++; for(int k=j;k<=i;k++)mn[k+1]=t++; i=j; } } for(int i=n;i>0;i--)if(!mn[i])mn[i]=t++; for(int i=1;i<=n;i++)printf("%d%c",mn[i]," "[i==n]); for(int i=1;i<=n;i++)printf("%d%c",mx[i]," "[i==n]); for(int i=1;i<=n;i++)mx[i]=mn[i]=0; } return 0; }
E. 1-Trees and Queries【ST表】

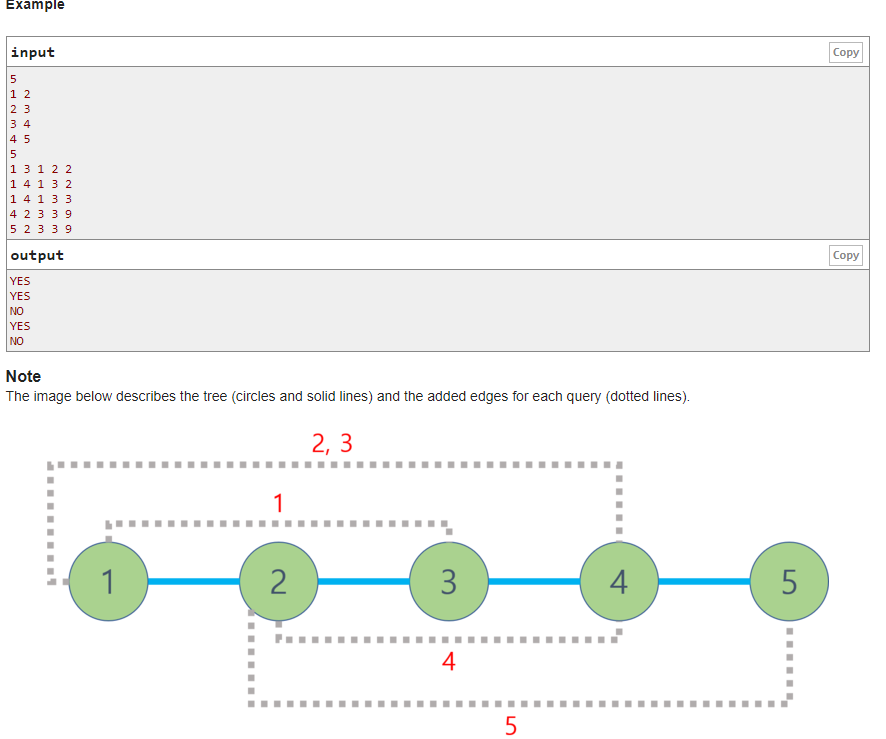
题意:给定一棵树,现在有q个询问,每次询问在a.b之间连一条额外的边之后,是否存在行走路径满足x->y的长度为k,边可以重复行走
题解:首先找到x->y的最短路,显然有两种情况,一种是不经过额外连边,那么就是树上原始路径x->y;
另一种是经过额外连边,那么又分两种情况,一钟x->a->b->y,一种x->b->a->y
将这些路径的长度求出来,因为边可以重复行走,所以到达y点后可以在相邻点来回走,每来回一次+2长度
因此需要求出奇数长度的最短路和偶数长度的最短路
最终根据k的奇偶性和是否比最短路长且是否多出来的长度是2的倍数来判断是否存在方案
#include<iostream> #include<cstdio> #include<cstdlib> using namespace std; int n,m; class Tree { public: struct T { int s,t; }t[100001*2]; int head[100001],nxt[100001*2],r; void Build(int ts,int tt); }tree; class Lca { public: int dp[100001]; int dfsa[100001*2],dfsan; int lcaa[100001*10],lcan,lcahead[100001]; int to_normal_i[100001],to_lca_i[100001]; int f[100001*10][21]; void Dfs1(int last,int now,int &bh,int dep); void Dfs2(int last,int now); void Work(); void Rmq(); int Ask(int s,int t); }lca; int dis(int s,int t){return lca.dp[s]+lca.dp[t]-2*lca.dp[lca.Ask(s,t)];} int main() { int ts,tt; scanf("%d",&n); for(int i=1;i<n;i++) { scanf("%d%d",&ts,&tt); tree.Build(ts,tt); } lca.Work(); scanf("%d",&m); int x,y,k; for(int i=1;i<=m;i++) { scanf("%d%d%d%d%d",&x,&y,&ts,&tt,&k); int l1=dis(ts,tt); int l2=dis(ts,x)+dis(y,tt)+1; int l3=dis(ts,y)+dis(x,tt)+1; int ji=1000000001,ou=1000000001; if(l1&1)ji=min(ji,l1); else ou=min(ou,l1); if(l2&1)ji=min(ji,l2); else ou=min(ou,l2); if(l3&1)ji=min(ji,l3); else ou=min(ou,l3); if(k&1) { if(k>=ji && (k-ji)%2==0)printf("YES "); else printf("NO "); } else { if(k>=ou && (k-ou)%2==0)printf("YES "); else printf("NO "); } } return 0; } //class Tree void Tree::Build(int ts,int tt) { t[++r].s=ts;t[r].t=tt; nxt[r]=head[ts];head[ts]=r; t[++r].s=tt;t[r].t=ts; nxt[r]=head[tt];head[tt]=r; } //class Lca void Lca::Dfs1(int last,int now,int &bh,int dep) { dp[now]=dep; dfsa[++dfsan]=bh; int tbh=bh,t1;bh++; to_lca_i[now]=tbh; to_normal_i[tbh]=now; t1=tree.head[now]; while(t1) { if(tree.t[t1].t!=last)Dfs1(now,tree.t[t1].t,bh,dep+1); t1=tree.nxt[t1]; } dfsa[++dfsan]=tbh; } void Lca::Dfs2(int last,int now) { lcaa[++lcan]=to_lca_i[now]; lcahead[now]=lcan; int t1=tree.head[now]; while(t1) { if(tree.t[t1].t!=last) { Dfs2(now,tree.t[t1].t); lcaa[++lcan]=to_lca_i[now]; } t1=tree.nxt[t1]; } } void Lca::Work() { int tbh=1; Dfs1(0,1,tbh,0); Dfs2(0,1); Rmq(); } void Lca::Rmq() { for(int i=1;i<=lcan;i++)f[i][0]=lcaa[i]; for(int j=1;(1<<j)<=lcan;j++) for(int i=1;i+(1<<j)-1<=lcan;i++) f[i][j]=min(f[i][j-1],f[i+(1<<(j-1))][j-1]); } int Lca::Ask(int s,int t) { s=lcahead[s];t=lcahead[t]; if(s>t)swap(s,t); int len,tpow=0; len=t-s+1; while((1<<tpow)<=len)tpow++;tpow--; return to_normal_i[min(f[s][tpow],f[t-(1<<tpow)+1][tpow])]; }
F2. Animal Observation (hard version)

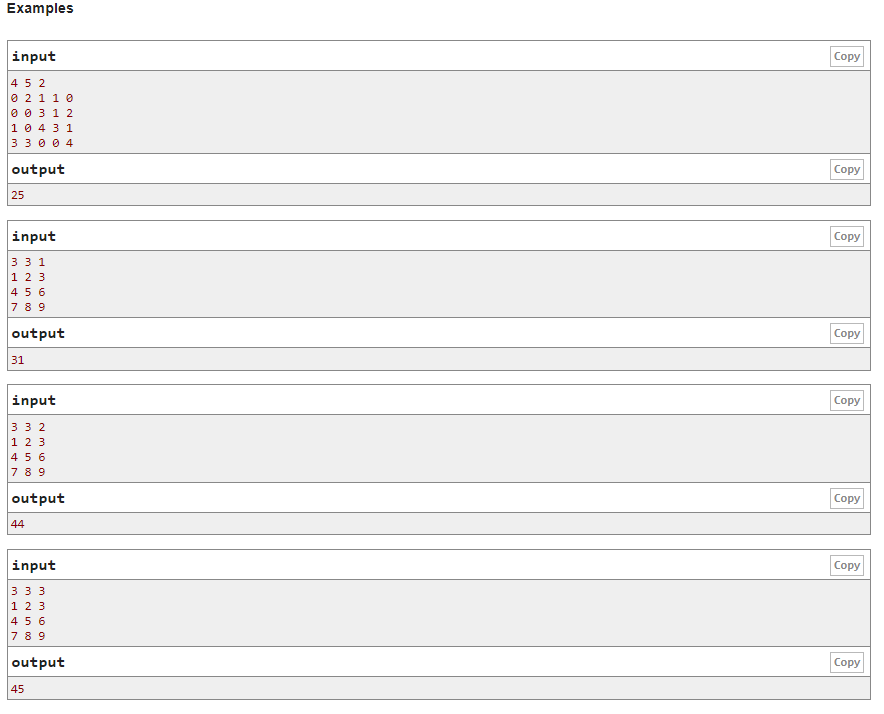
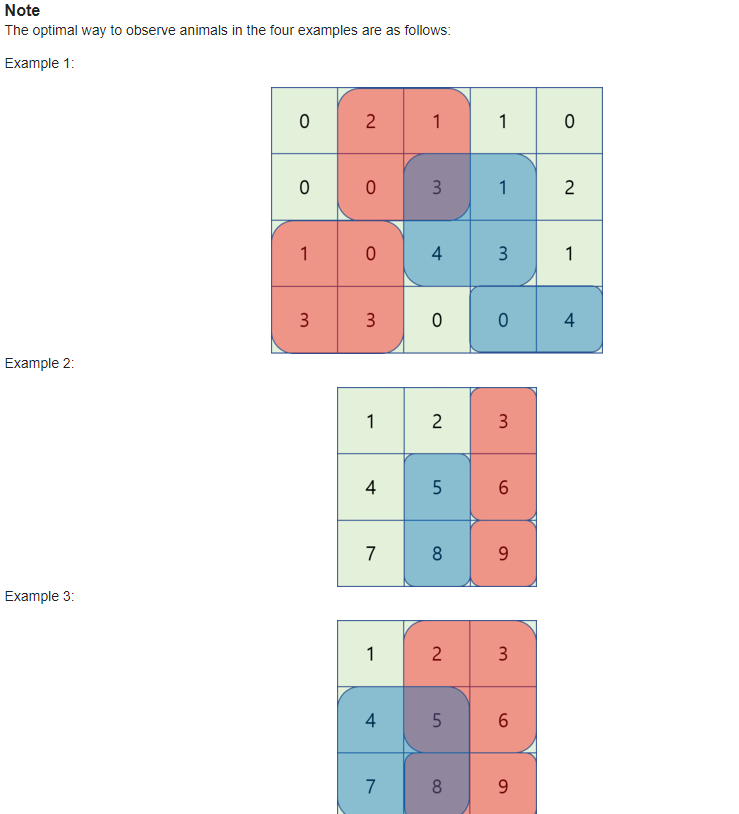
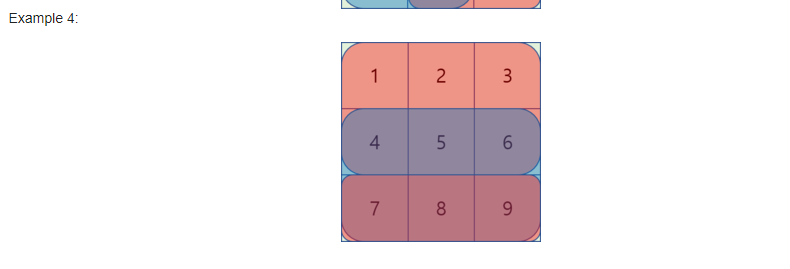
待填坑