Mobile Computing UVA

回溯法+搜索对象的选取

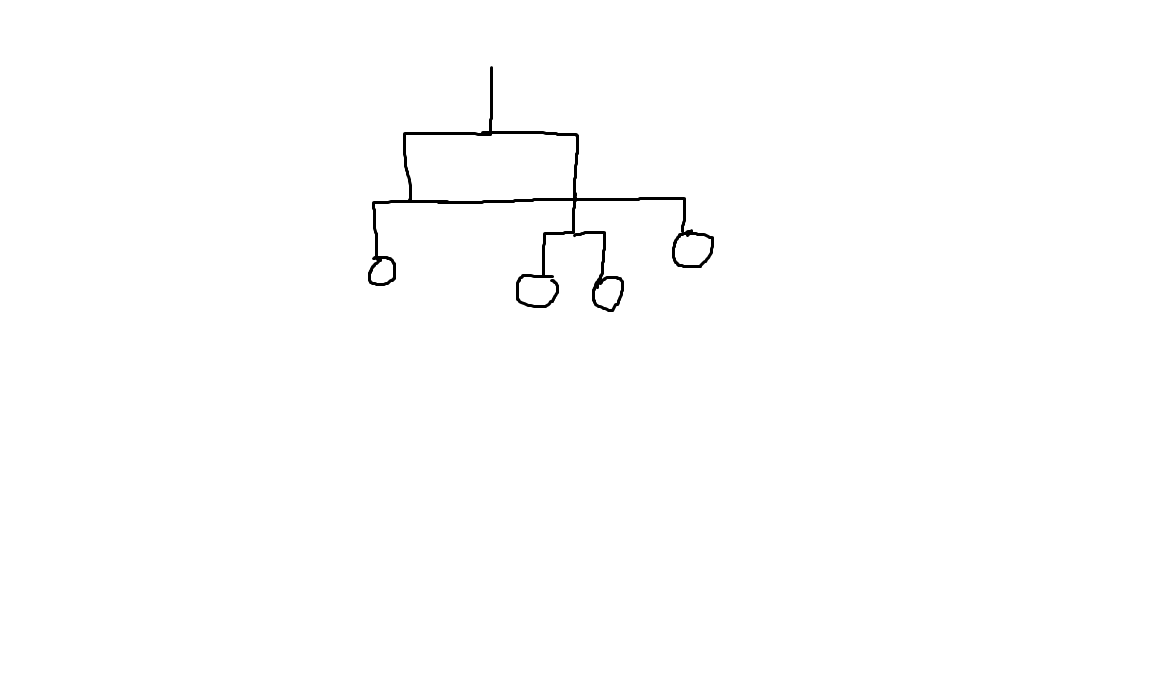
天平模型可看作一个只要有子树则左右子树必然全有的树，则枚举每个天平的实例（也就是每个集合）就是枚举所有可能的每棵树。

每次选择当前集合的一个子集作为左子树，当前总集作为当前根，来创建树。

通过dfs后续遍历树，在从最深处叶子返回到根时，存储每个当前总集的根到最左端和最右端的距离；

由递推式 当前根到最左端/右端距离=其左子树到最左端+根到左子树       右则是：右子树到最右端+根到右子树；

因为天平可以重叠，所以要考虑一个天平a的 左子天平al的到其右子树alr的长度减掉它到al的那一段还比右侧正常情况长！左侧同理

并且如果天平已经访问过，则不再重复访问，进行回溯！具体的看代码注解。

// UVa1354 Mobile Computing
// Rujia Liu
#include<cstdio>
#include<cstring>
#include<vector>
using namespace std;

struct Tree {
  double L, R; // distance from the root to the leftmost/rightmost point
  Tree():L(0),R(0) {}
};

const int maxn = 6;

int n, vis[1<<maxn];
double r, w[maxn], sum[1<<maxn];
vector<Tree> tree[1<<maxn]; //每个子集都对应了一个 vector<tree> 容器，来存

void dfs(int subset) {
  if(vis[subset]) return;    //不重复访问访问过的子集，因为这个dfs只记录每个subset作为根时 到其左右子树最左右叶子部分的长度，所以重复访问没有意义，完全一样！
  vis[subset] = true;        //

  bool have_children = false;
  for(int left = (subset-1)&subset; left; left = (left-1)&subset) {     //去left中所有与subset相同的元素。若不存在则退出循环
    have_children = true;//如果存在，则将子集标志致真                //就是遍历集合的所有子集，真实没想到还能这样写！但是这样写会重复不少次，比如11000001这个集合。因为前边的1捡不到，所以会使包含头尾元素的子集dfs调用很多次

    int right = subset^left;//右子集为左子集相对总集的补集！（这个我会！）
    double d1 = sum[right] / sum[subset];//d1为左边的天平杆的长度
    double d2 = sum[left] / sum[subset];//d2为右边的

    dfs(left); dfs(right);//然后递归求left right子树的。（只要没走到叶子结点时一定会走到这一步，即这一步的下一步一定是执行完 该子树的操作后进行。

    for(int i = 0; i < tree[left].size(); i++)//对于当前left，right 已经进行判断过的结点或者叶子结点才用（其实这一点是必然的，这一步是在对子树dfs之后的，算是后序遍历）
      for(int j = 0; j < tree[right].size(); j++) {
        Tree t;     //注意接下来的两个max（）函数！！并不是想求每个左右子树中的末端结点到 其自己根的长度中的最长的！而是只用来判断每个左右
        t.L = max(tree[left][i].L + d1, tree[right][j].L - d2);//后边那个的那部分来处理重叠情况，就是如果右子树right的子树太长了，比在减去d2后都超过比左边leift向左生长的子树长度了
        t.R = max(tree[right][j].R + d2, tree[left][i].R - d1);//同理，处理left的有子树太长    //这一步判断想的是真的细。
        if(t.L + t.R < r) tree[subset].push_back(t);//如果符合条件，记录当前集合作为某层根结点（只要符合条件的全要！，并不是存当前最大）
      }
  }

  if(!have_children) tree[subset].push_back(Tree());//递归到叶子结点时，为该叶子结点创建Tree（都是0，逻辑上一个叶子结点不应该有左右子树的天平杆）来记录他从root到最左右天平长度
}

int main() {
  int T;
  scanf("%d", &T);
  while(T--) {
    scanf("%lf%d", &r, &n);
    for(int i = 0; i < n; i++) scanf("%lf", &w[i]);
    for(int i = 0; i < (1<<n); i++) {
      sum[i] = 0;
      tree[i].clear();
      for(int j = 0; j < n; j++)
        if(i & (1<<j)) sum[i] += w[j];//sum[0]-sum[n] 为w[j]每个集合重量
    }

    int root = (1<<n)-1;    //设根为全集
    memset(vis, 0, sizeof(vis));
    dfs(root);//通过dfs

    double ans = -1;
    for(int i = 0; i < tree[root].size(); i++)
      ans = max(ans, tree[root][i].L + tree[root][i].R);//从tree[root]中筛选哪种 左右子集选择最大
    printf("%.10lf
", ans);
  }
  return 0;
}