1 概述
二叉搜索树,又称二叉查找树,二叉排序树。其最显著的特点就是:对于每一个结点,其左子树所有结点的权值都小于它自身的权值,其右子树所有结点的权值都大于它自身的权值。
下图中的这棵树就是一棵二叉搜索树:
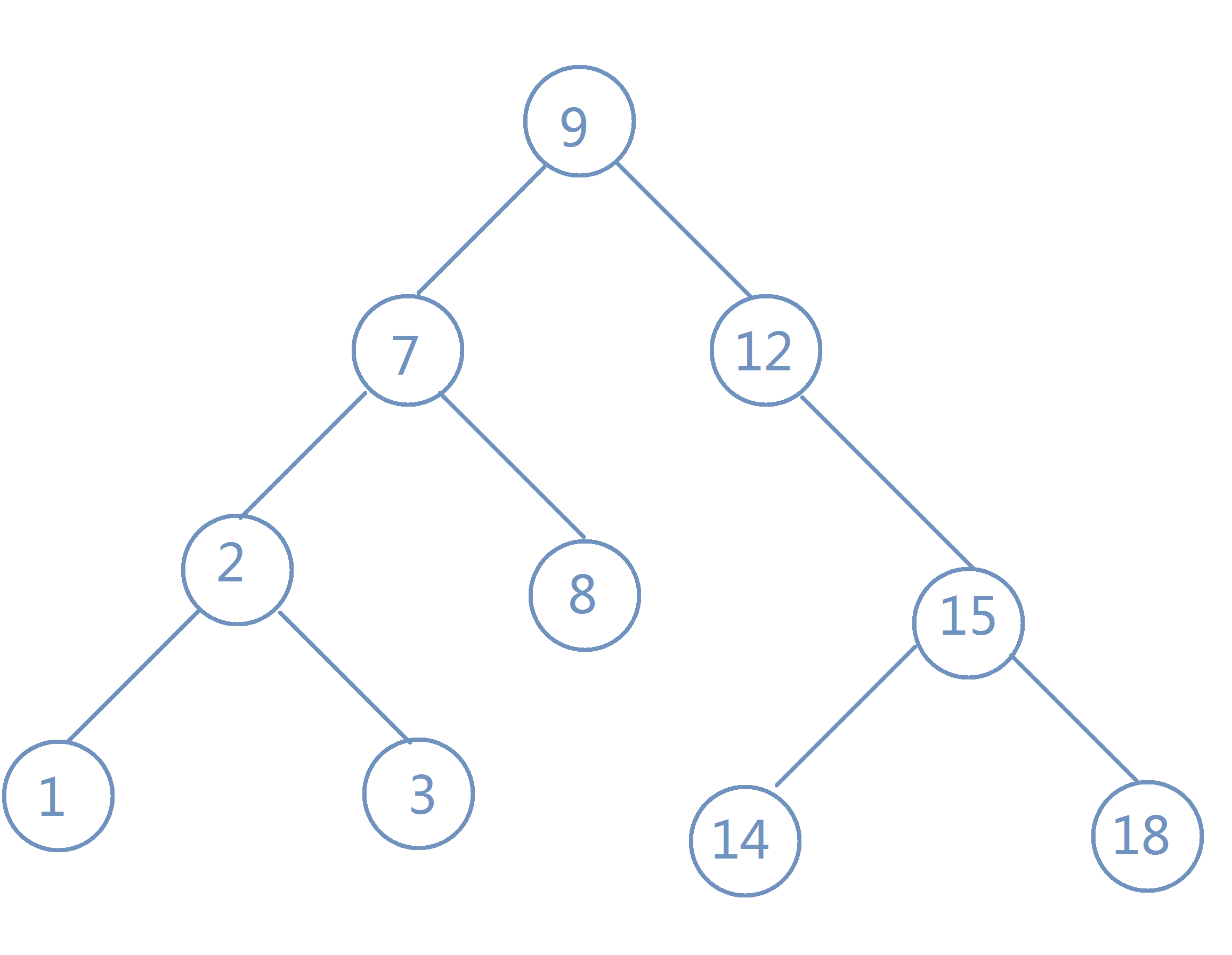
(结点中的数字表示该结点的权值)
可以发现,任意一棵二叉搜索树的中序遍历都是一个有序数列。
二叉搜索树的功能十分强大,这里只介绍几种基本操作。
2 基本操作
2.0 基本变量与函数的定义
代码如下:
struct Node//这是存储二叉搜索树结点的结构体 { int l;//存储该结点的左儿子 int r;//存储该结点的右儿子 int val;//存储该结点的权值 int siz;//存储该结点的子树大小 int sum;//存储该节点的副本数 }s[SIZE];//SIZE为结点的总个数 void UpdateNode(int x)//更新该结点子树大小的函数 { //当前结点的子树大小等于它左右儿子的子树大小加上它本身的大小 s[x].siz=s[s[x].l].siz+s[s[x].r].siz+s[x].sum; } int tot=0,root=0;//tot用来记录当前结点新建到哪个数组下标了,root为当前的树根
所谓“副本数”是指一个数重复出现的次数,因为在实际应用中,常常会出现在二叉搜索树中多次插入同一个值的情况,但严格来说,二叉搜索树中是不允许出现权值相同的结点的,所以我们要加上这一个变量来记录每个结点所代表的的值出现了多少次。对于插入值重复的问题,还有一种解决方案,那就是当插入的权值等于当前结点的权值时,就将其插入到当前结点的右子树中。这样虽然也能解决问题,但破坏了二叉搜索树的性质,因为这使得右子树所有结点的权值不一定大于当前结点的权值了。在这篇文章中我将采用第一种方案。
有人可能会问,为什么要记子树大小呢?看到后面你就明白了。
什么?tot是干嘛的也不清楚?还是那句话,看到后面你就明白了。
2.1 新建结点
代码如下:
int NewNode(int val)//以val为权值新建一个结点 { tot++;//开辟一个新空间 s[tot].val=val;//初始化新结点权值 s[tot].l=s[tot].r=0;//初始化新结点左右儿子 s[tot].siz=s[tot].sum=1;//初始化新结点的子树大小和副本数 return tot;//返回新节点的数组下标(这是为了让以后的操作更方便) }
tot的作用这时就显现出来了,它可以理解成是用来记录当前数组用到哪了以及开辟新的存储空间的。
这个操作还是很易懂的,就是各种初始化。
2.2 建树
代码如下:
void BuildTree() { NewNode(-INF),NewNode(INF);//插入一个极小值和一个极大值 root=1,s[root].r=2;//初始化树根以及树根的右儿子 UpdateNode(root);//记得更新树根的子树大小 }
建树操作很简单,在二叉搜索树中插入一个极大值和一个极小值即可。为什么要这样弄呢?因为这样可以避免越界以及减少对边界情况的判断,使代码更加简洁。
2.3 插入
代码如下:
void InsertNode(int &p,int val)//p为当前结点,val为待插入权值【注意p是引用】 { if(p==0) { p=NewNode(val); return; }//如果走到最后发现没有东西,就新建一个结点来存储 if(val==s[p].val) { s[p].siz++,s[p].sum++; return; }//如果找到了权值重复的结点将其副本数加1即可 if(val<s[p].val) InsertNode(s[p].l,val);//如果待插入结点的权值小于当前结点的权值就往左子树中插入 else InsertNode(s[p].r,val);//如果待插入结点的权值大于当前结点的权值就往右子树中插入 UpdateNode(p);//记得更新当前结点的子树大小 }
插入操作的实现很容易,就是在二叉搜索树中找到对应的位置进行操作。值得一提的是,上述代码中的p是一个引用(如果不知道“引用”是什么可以上网查一下),这样的话,在给p赋值的同时也同时更新了新结点父亲的左儿子或右儿子,这就不用返回新节点的下标了,代码会更加简洁。
2.4 查询某一个值的排名
这里我们所说的某一个数排名是指小于这个数的数的个数,这时候,每个结点的子树大小就派上用场了。这里我们可以分四种情况讨论:
1.如果当前要查询的值大于当前结点的权值,就说明当前结点左子树的所有结点的权值以及当前结点本身的权值都小于要查询的值,所以我们可将其排名加上当前结点的左子树大小以及当前结点本身的大小,并继续在当前结点的右子树找。
2.如果当前要查询的值小于当前结点的权值,那么排名将不会更新,因为你并不知道在这里究竟有多少结点的权值小于要查询的值,然后要继续往当前结点的左子树找。
3.如果当前要查询的值等于当前结点的权值,直接返回当前结点的左子树大小加一。
4.如果在树中没有找到要查询的值,返回1即可。
最好自己再画图理解一下。
代码如下:
int GetVDPM(int p,int val)//p为当前结点,val为要查询的值 { if(p==0) return 1;//如果没找到就返回1 //如果当前要查询的值等于当前结点的权值,直接返回当前结点的左子树大小加一。 if(val==s[p].val) return s[s[p].l].siz+1; //如果当前要查询的值小于当前结点的权值,继续往当前结点的左子树找。 if(val<s[p].val) return GetVDPM(s[p].l,val); //如果当前要查询的值大于当前结点的权值,将其排名加上当前结点的左子树大小以及当前结点本身的大小,继续在当前结点的右子树找。 return GetVDPM(s[p].r,val)+s[s[p].l].siz+s[p].sum; }
2.5 查询排名为某个数的值是多少
这个操作思路和上一个操作的思路较为相似,这里就不再赘述,大家自行结合代码理解即可。
代码如下:
int GetPMWRDS(int p,int rank)//p为当前结点,要查询排名为rank的数 { if(p==0) return INF;//如果这个排名太大了,没找到相对应的值,就返回极大值 if(s[s[p].l].siz>=rank) return GetPMWRDS(s[p].l,rank);//如果当前节点的左子树大小大于待处理排名,就在其左子树中继续处理 if(s[s[p].l].siz+s[p].sum>=rank) return s[p].val;//找到了,返回当前节点的权值 return GetPMWRDS(s[p].r,rank-s[s[p].l].siz-s[p].sum);//在右子树中继续处理 }
2.6 查询某一个数的前驱或后继
这里先给出前驱与后继的定义:
结点x的前驱:权值比x小的结点中权值最大的结点。
结点x的后继:权值比x小的结点中权值最大的结点。
由于求前驱的过程与求后继的过程十分相似,这里只给出求前驱的过程,求后继的过程留给大家自行思考。
求前驱的步骤如下:
0.假设我们要寻找x的前驱。
1.在二叉搜索树中查找x,每经过一个点都试图更新答案。
2.如果没找到x,就返回当前答案。
3.如果找到了x,但x没有左子树,也返回当前答案。
4.如果找到了x,且x有左子树,就从x的左结点出发一直往右走,最下面那个结点就是x的后继。
(仔细想想为什么这样是正确的)。
代码如下:
int GetPre(int val)//求val的前驱 { int ans=1,p=root;//s[1].val=-INF while(p)//查找权值为val的节点 { if(val==s[p].val)//如果找到了 { if(s[p].l)//如果它有左儿子 { p=s[p].l; while(s[p].r) p=s[p].r;//就沿着它的左儿子的右儿子向右一直走下去 ans=p;//最下面的那个便是其前驱 } break;//退出循环 } if(s[p].val<val&&s[p].val>s[ans].val) ans=p;//每经过一个节点就试图更新答案 p=(val<s[p].val)?s[p].l:s[p].r;//向下查找 } return s[ans].val;//返回答案 }
2.7 删除
删除是一个比较麻烦的操作,删除操作的步骤如下:
0.假设我们删除的结点是x。
1.在二叉搜索树中查找x。
2.如果没有找到x,直接结束。
3.如果找到了x,且x的副本数大于1,直接将x的副本数减1。
4.如果找到了x,而且x的副本数等于1,并且x只有左子树,就让x的左儿子代替x的位置。
5.如果找到了x,而且x的副本数等于1,并且x只有右子树,就让x的右儿子代替x的位置。
6.如果找到了x,而且x的副本数等于1,并且x既有左子树又有右子树,就让x的后继代替x的位置(想想为什么一定要用x的后继代替x的位置)。
7.记得更新所涉及到的结点的子树大小。
代码如下:
void RemoveNode(int &p,int val)//p为当前结点,val为要删除的值 { if(p==0) return;//如果没找到待删除的值,直接结束 //查找待删除的值 if(val<s[p].val) RemoveNode(s[p].l,val); if(val>s[p].val) RemoveNode(s[p].r,val); if(val==s[p].val)//如果找到了 if(s[p].sum>1) s[p].sum--;//如果其副本数大于1,直接将其副本数减一即可 else if(s[p].l==0) p=s[p].r;//如果没有左子树,直接令其右儿子代替它 【注意p是引用】 else if(s[p].r==0) p=s[p].l;//如果没有右子树,直接令其左儿子代替它 【注意p是引用】 else //如果既有左子树又有右子树 { int k=s[p].r; while(s[k].l) k=s[k].l;//寻找其后继 int u=s[k].sum;//将其后继的副本数备份 s[k].sum=1,RemoveNode(root,s[k].val);//然后将其后继的副本数改为1,直接删除 //接着令其后继的左右儿子等于待删除节点的左右儿子,并将其副本数复原 s[k].l=s[p].l,s[k].r=s[p].r,s[k].sum=u; p=k;//最后令其后继代替待删除节点位置 【注意p是引用】 } UpdateNode(p);//更新当前节点的子树大小 }
3 时间复杂度分析
3.1 随机数据下的时间复杂度
在随机数据下,二叉搜索树的期望深度是log2n的,而二叉搜索树的一次操作时间复杂度就是它自己的深度,所以在随机数据下,二叉搜索树每次操作的期望时间复杂度就是O(log2n)。这个时间复杂度还是相当优秀的。
下图中的这棵二叉搜索树就是一棵最理想的二叉搜索树:

3.2 退化
不过不要高兴得太早,二叉搜索树是很容易退化的,如果数据极端一点,往二叉搜索树里插入一个有序数列的话,二叉搜索树就会变成下面这个样子:

这样的话,树的深度就是n了,二叉搜索树一次操作的时间复杂度也就退化为O(n)了,这个时间复杂度显然是难以接受的。
3.3 解决方案
二叉搜索树时间复杂度退化的原因很明显,是因为树十分不平衡,为了维持二叉搜索树在平衡状态下单次操作O(log2n)的优秀复杂度,我们可以使用二叉搜索树的升级版——平衡树。常见的平衡树有Treap、Splay等,它们的原理都是用某种方式来使二叉搜索树变得更加平衡从而保证时间复杂度,这里就不展开讲了,有兴趣的同学可以自行搜索相关资料学习。
4 练习题
二叉搜索树裸题,但直接写二叉搜索树最后一个点会超时(平衡树才是正解),如果除了最后一个点都对了就说明程序没问题,练习的时候注意一下就好。
代码:
#include<iostream> #include<cstdio> #include<cstdlib> #include<fstream> using namespace std; const int INF=1e9; struct Node { int l; int r; int val; int siz; int sum; }s[100005]; int tot=0,root=0; int NewNode(int val) { s[++tot].val=val; s[tot].l=s[tot].r=0; s[tot].siz=s[tot].sum=1; return tot; } void UpdateNode(int x) { s[x].siz=s[s[x].l].siz+s[s[x].r].siz+s[x].sum; } void BuildTree() { NewNode(-INF),NewNode(INF); root=1,s[root].r=2; UpdateNode(root); } void InsertNode(int &p,int val) { if(p==0) { p=NewNode(val); return; } if(val==s[p].val) { s[p].siz++,s[p].sum++; return; } if(val<s[p].val) InsertNode(s[p].l,val); else InsertNode(s[p].r,val); UpdateNode(p); } void RemoveNode(int &p,int val) { if(p==0) return; if(val<s[p].val) RemoveNode(s[p].l,val); if(val>s[p].val) RemoveNode(s[p].r,val); if(val==s[p].val) if(s[p].sum>1) s[p].sum--; else if(s[p].l==0) p=s[p].r; else if(s[p].r==0) p=s[p].l; else { int k=s[p].r; while(s[k].l) k=s[k].l; int u=s[k].sum; s[k].sum=1,RemoveNode(root,s[k].val); s[k].l=s[p].l,s[k].r=s[p].r,s[k].sum=u; p=k; } UpdateNode(p); } int GetVDPM(int p,int val) { if(p==0) return 1; if(val==s[p].val) return s[s[p].l].siz+1; if(val<s[p].val) return GetVDPM(s[p].l,val); return GetVDPM(s[p].r,val)+s[s[p].l].siz+s[p].sum; } int GetPMWRDS(int p,int rank) { if(p==0) return INF; if(s[s[p].l].siz>=rank) return GetPMWRDS(s[p].l,rank); if(s[s[p].l].siz+s[p].sum>=rank) return s[p].val; return GetPMWRDS(s[p].r,rank-s[s[p].l].siz-s[p].sum); } int GetPre(int val) { int ans=1,p=root; while(p) { if(val==s[p].val) { if(s[p].l) { p=s[p].l; while(s[p].r) p=s[p].r; ans=p; } break; } if(s[p].val<val&&s[p].val>s[ans].val) ans=p; p=(val<s[p].val)?s[p].l:s[p].r; } return s[ans].val; } int GetSuc(int val) { int ans=2,p=root; while(p) { if(val==s[p].val) { if(s[p].r) { p=s[p].r; while(s[p].l) p=s[p].l; ans=p; } break; } if(s[p].val>val&&s[p].val<s[ans].val) ans=p; p=(val<s[p].val)?s[p].l:s[p].r; } return s[ans].val; } int main() { int n=0; scanf("%d",&n); BuildTree(); for(int i=1;i<=n;i++) { int x=0,y=0; scanf("%d%d",&x,&y); if(x==1) InsertNode(root,y); if(x==2) RemoveNode(root,y); if(x==3) printf("%d ",GetVDPM(root,y)-1); if(x==4) printf("%d ",GetPMWRDS(root,y+1)); if(x==5) printf("%d ",GetPre(y)); if(x==6) printf("%d ",GetSuc(y)); } return 0; }
5 参考资料
《算法竞赛进阶指南》(李煜东著)第0x46节。