Matlab实现抽样定理
正弦信号的抽样:
首先时间跨度选择 -0.2 到 0.2,间隔0.0005取一个点,原信号取 sin(2π*60t) ,则频率为60Hz。
由于需要输出原始信号的波形,我选择了手动编写代码进行傅里叶变换,有公式origin_F = origin * exp(-1i * t' * W) * 0.0005 傅里叶变换后的值,并取绝对值。
采样则调整取点的间隔就ok了。
恢复波形不太懂,在网上找到的方法:
f_covery = f_uncovery * sinc((1/Nsampling) * (ones(length(n_sam), 1) * t - n_sam' * ones(1, length(t))));
出处为:
http://www.mathsky.cn/wiki/index.php?search-fulltext-title-%D0%C5%BA%C5%BB%D6%B8%B4--all-0-within-time-desc-1
最后则可以输出波形和原始信号进行对比分析。
混合信号的抽样:
这里和正弦信号相比,只是待抽样信号不同了而已,但是混合信号我用的是正弦和余弦的叠加
sin(2 * pi * 60 * t) + cos(2 * pi * 25 * t) + sin(2 * pi * 30 * t)
由于抽样频率没变,依然是80Hz、121Hz、150Hz,所以得到的结果和上面的是不一样的
下面的结果图会有相应的分析
实现效果
正弦信号:

恢复的波形为
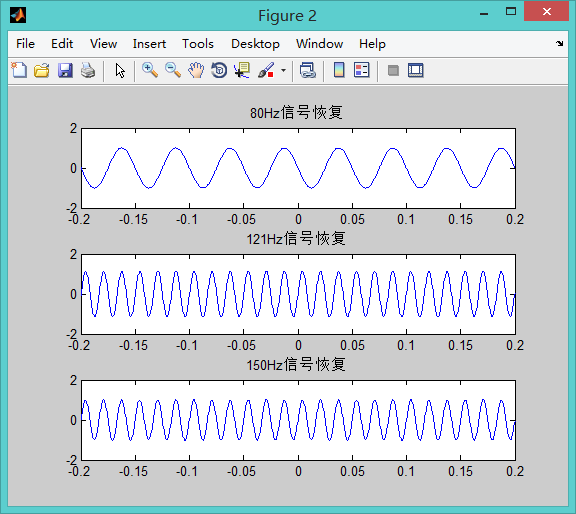
对比80Hz的信号和121Hz的信号可知,原信号为60Hz的信号,至少需要120Hz才能不失真地恢复信号,由图可得,80Hz的信号虽然还是正弦信号,但是相位信息已经失真了。121Hz和150Hz的抽样信息则准确地恢复了原信号
混合信号:
因为只有原信号和下面的代码不一样,所以节省国家树木资源便不全部截图代码了。
不一样的地方为原信号为混合信号:
%% 设置原始信号
t = -0.2 : 0.0005 : 0.2;
N = 1000;
k = -N : N;
W = k * 2000 / N;
origin = sin(2 * pi * 60 * t);% 原始信号为正弦信号
origin_F = origin * exp(-1i * t' * W) * 0.0005;% 傅里叶变换
origin_F = abs(origin_F);% 取正值
figure;
subplot(4, 2, 1); plot(t, origin); title('原信号时域');
subplot(4, 2, 2); plot(W, origin_F); title('原信号频域');
运行效果图:

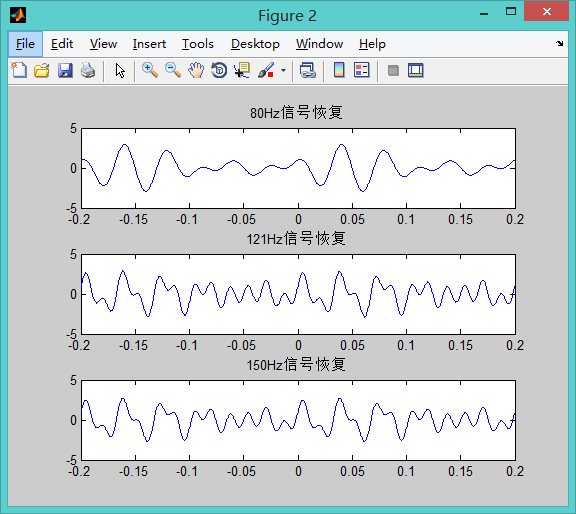
这个信号明显地可以看出80Hz采样的失真情况。由于混合信号中频率最高的那个信号为60Hz,因此也是至少需要120Hz才能不失真地恢复原始信号。
代码实现
clear all
clc
%% 设置原始信号
t = -0.2 : 0.0005 : 0.2;
N = 1000;
k = -N : N;
W = k * 2000 / N;
origin = sin(2 * pi * 60 * t) + cos(2 * pi * 25 * t) + sin(2 * pi * 30 * t);% 原始信号为正弦信号叠加
origin_F = origin * exp(-1i * t' * W) * 0.0005;% 傅里叶变换
origin_F = abs(origin_F);% 取正值
figure;
subplot(4, 2, 1); plot(t, origin); title('原信号时域');
subplot(4, 2, 2); plot(W, origin_F); title('原信号频域');
%% 对原始信号进行80Hz采样率采样
Nsampling = 1/80; % 采样频率
t = -0.2 : Nsampling : 0.2;
f_80Hz = sin(2 * pi * 60 * t) + cos(2 * pi * 25 * t) + sin(2 * pi * 30 * t); %采样后的信号
F_80Hz = f_80Hz * exp(-1i * t' * W) * Nsampling; % 采样后的傅里叶变换
F_80Hz = abs(F_80Hz);
subplot(4, 2, 3); stem(t, f_80Hz); title('80Hz采样信号时域');
subplot(4, 2, 4); plot(W, F_80Hz); title('80Hz采样信号频域');
%% 对原始信号进行121Hz采样率采样
Nsampling = 1/121; % 采样频率
t = -0.2 : Nsampling : 0.2;
f_80Hz = sin(2 * pi * 60 * t) + cos(2 * pi * 25 * t) + sin(2 * pi * 30 * t); %采样后的信号
F_80Hz = f_80Hz * exp(-1i * t' * W) * Nsampling; % 采样后的傅里叶变换
F_80Hz = abs(F_80Hz);
subplot(4, 2, 5); stem(t, f_80Hz); title('121Hz采样信号时域');
subplot(4, 2, 6); plot(W, F_80Hz); title('121Hz采样信号频域');
%% 对原始信号进行150Hz采样率采样
Nsampling = 1/150; % 采样频率
t = -0.2 : Nsampling : 0.2;
f_80Hz = sin(2 * pi * 60 * t) + cos(2 * pi * 25 * t) + sin(2 * pi * 30 * t); %采样后的信号
F_80Hz = f_80Hz * exp(-1i * t' * W) * Nsampling; % 采样后的傅里叶变换
F_80Hz = abs(F_80Hz);
subplot(4, 2, 7); stem(t, f_80Hz); title('150Hz采样信号时域');
subplot(4, 2, 8); plot(W, F_80Hz); title('150Hz采样信号频域');
%% 恢复原始信号
% 从80Hz采样信号恢复
figure;
n = -100 : 100;
Nsampling = 1/80;
n_sam = n * Nsampling;
f_uncovery = sin(2 * pi * 60 * n_sam) + cos(2 * pi * 25 * n_sam) + sin(2 * pi * 30 * n_sam);
t = -0.2 : 0.0005 : 0.2;
f_covery = f_uncovery * sinc((1/Nsampling) * (ones(length(n_sam), 1) * t - n_sam' * ones(1, length(t))));
subplot(3, 1, 1); plot(t, f_covery); title('80Hz信号恢复');
% 从121Hz采样信号恢复
Nsampling = 1/121;
n_sam = n * Nsampling;
f_uncovery = sin(2 * pi * 60 * n_sam) + cos(2 * pi * 25 * n_sam) + sin(2 * pi * 30 * n_sam);
t = -0.2 : 0.0005 : 0.2;
f_covery = f_uncovery * sinc((1/Nsampling) * (ones(length(n_sam), 1) * t - n_sam' * ones(1, length(t))));
subplot(3, 1, 2); plot(t, f_covery); title('121Hz信号恢复');
% 从150Hz采样信号恢复
Nsampling = 1/150;
n_sam = n * Nsampling;
f_uncovery = sin(2 * pi * 60 * n_sam) + cos(2 * pi * 25 * n_sam) + sin(2 * pi * 30 * n_sam);
t = -0.2 : 0.0005 : 0.2;
f_covery = f_uncovery * sinc((1/Nsampling) * (ones(length(n_sam), 1) * t - n_sam' * ones(1, length(t))));
subplot(3, 1, 3); plot(t, f_covery); title('150Hz信号恢复');