二叉树的生成

1. 通过前序和中序生成

　　中序：leftTree, root, rightTree

　　前序：root, leftTree, rightTree

　　思路：很显然，通过前序序列，我们可以很容易知道树的root，然后通过查找中序序列中相应的root位置，便可以确定该root的左右子树。然后借助递归思想，对左右子树进行相同的操作，便能够构造出这棵树。为此，我们需要确定几个位置，即前序遍历的根节点位置rootPos，其左子树的根节点位置和右节点位置；以及对应的中序遍历序列中树的左右边界，以及根节点的位置。

先根据递归思想，写出递归方程：

Bitree *buildTree(vector<int> preOrder, int preRootPos, vector<int> inOrder, int inOrderLeftBound, int inOrderRightBound){
  if(inOrderLeftBound > inOrderRightBound){
    return nullptr;
  }
  Bitree *root = new Bitree(preOrder[preRootPos]);
  int inOrderRootPos = inOrder.find();
  root->left = buildTree(preOrder, leftTreeRootPos, inOrder, inOrderLeftBound, inOrderRootPos-1);
  root->right = buildTree(preOrder, rightTreeRootPos, inOrder, inOrderRootPos+1, inOrderRightBound);
  return root;
}

可知，我们需要确定leftTreeRootPOS、rightTreeRootPOS来正确定位左右子树在前序序列中的位置，以完成递归算法的正确分割。为了确定这两个值，先画图：

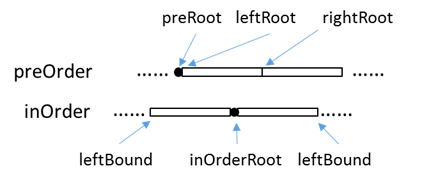
　　其中，leftTreeRootPos很好确定，即preRootPos+1；对rightTreeRootPos，则需要先知道左子树的长度，为此，可使用图中中序序列的inOrderRoot-leftBound求解，即rightTreeRootPos=preRoot+(inOrderRoot-leftBound)+1。到此，递归便能正常进行下去。

由此，算法为

Bitree *buildTree(vector<int> preOrder, int preRootPos, vector<int> inOrder, int inOrderLeftBound, int inOrderRightBound){
  if(inOrderLeftBound > inOrderRightBound){
    return nullptr;
  }
  Bitree *root = new Bitree(preOrder[preRootPos]);
  int inOrderRootPos = find(inOrder.begin(), inOrder.end(), root->val)-inOrder.begin();//find has to be used like this
  root->left = buildTree(preOrder, preRootPos+1, inOrder, inOrderLeftBound, inOrderRootPos-1);
  root->right = buildTree(preOrder, preRootPos+(inOrderRootPos-inOrderLeftBound)+1, inOrder, inOrderRootPos+1, inOrderRightBound);
  return root;
}

注意：上图中的省略号不能省略，它反映了递归过程中的一般情况。在递归过程中，一棵小子树的序列在前序和中序序列中并非是左边界对其（及前序中的root位置和中序中的leftBound位置相同）的，若没有省略号，那么容易造成左对齐的误解，对后来左右子树的在前序序列中的位置产生误判。

2. 通过中序和后续生成

　　中序：leftTree, root, rigthTree

　　后续：leftTree, rightTree, root

　　和上面算法思想相似，只是注意左子树和右子树中的root在后序后列中的位置就好了。直接上代码：

Bitree *buildTree(vector<int> postOrder, int postRootPos, vector<int> inOrder, int inOrderLeftBound, int inOrderRightBound){
  if(inOrderLeftBound > inOrderRightBound){
    return nullptr;
  }
  Bitree *root = new Bitree(preOrder[postRootPos]);
  int inOrderRootPos = find(inOrder.begin(), inOrder.end())-inOrder.begin();
  root->left = buildTree(postOrder, postRootPos-(inOrderRootPos-inOrderLeftBound)-1, inOrder, inOrderLeftBound, inOrderRootPos-1);
  root->right = buildTree(preOrder, postRootPos-1, inOrder, inOrderRootPos+1, inOrderRightBound);
  return root;
}

 当然，最后提醒一句，生成了勿忘销毁。