目录:
常常在文章中看看某某满足xxx概率分布,具有什么特点,能得出什么结论。但是自己却总是想不起这些信息,有时也会混乱了分布。不查不知道啊,其实概率分布的知识还是很多的,种类也达到数十种,混淆也情有可原。
1.系列文章内容介绍
本系列文章将介绍两大类型的分布,分别是离散型分布和连续型分布。每个大类分布下还有很多小的分布。所有分布会以下面用思维导图固定的形式去表现出来。

注:非必要情况下,文章的公式均是定义为主,公式推导尽量不出现
2.关键名词理解
2.0 随机变量
在客观世界中,存在大量的随机现象,随机现象产生的结果构成了随机事件。用变量来描述随机现象的各个结果,就叫做随机变量。
随机变量有有限和无限的区分,一般又根据变量的取值情况分成离散型随机变量和非离散型随机变量(包括但不等于连续型随机变量),具体看其解释:
离散型随机变量: 有些随机变量,它全部可能取到的不相同的值是有限个或可列无限多个,也可以说概率以一定的规律分布在各个可能值上。这种随机变量称为"离散型随机变量",如抛硬币。
连续性随机变量: 连续型随机变量是指如果随机变量X的所有可能取值不可以逐个列举出来,而是取数轴上某一区间内的任一点的随机变量,如某日温度。
经过以上解释,可知下面的随机事件的分类情况:
| 随机变量类型 | 例子 |
|---|---|
| 离散型 | 抛硬币、掷色子、商品出现次品的个数 |
| 连续型 | 某一天的温度、某商品的寿命 |
2.1 描述数据概率相关名词
前面已经介绍了随机变量,按照其是否有限分为两种大类的分布。假设随机变量包含以下取值{a,b,c,d,e,f}.并假设其概率情况如下:

- 实际中,我们需要知道某个随机变量出现的概率,比如a出现的概率P(X=a)=0.03,这就出现后面描述某个点概率的
概率函数等概念。- 还有一种是我们想知道一组随机变量出现的概率,比如b,c,d出现的概率P(X={b,c,d})=0.218,这就出现后面描述某个区间概率的
分布函数等概念。- 连续型随机变量由于其变量的无穷,求概率时会引入积分概念,出现了
概率密度等概念。
注:分布函数与概率函数可以相互转换
2.1.1 概率函数
概率函数:用函数的形式来表达概率(一次只能表示一个取值的概率),比如可以用以下函数表示"抛硬币出现点数"事件的概率。
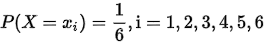
注:据查百度百科的概率分布函数词条,该词和概率分布函数是同义词,所以这样理解是对的,可参下面的概率分布函数。
2.1.2 分布函数
假设用X表示随机事件的概率,那么对于所有区间的概率均可以用{X<=x}来表示,如{X>x}~1-{X<=x} ; {a<X<=b} ~ {X<=b} - {X<=a}.
所以分布函数定义为:
设X是随机变量,对于任意实数x,则函数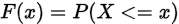 称为随机变量X的分布函数
称为随机变量X的分布函数
特点:
1.定义域为: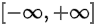 ,值域为[0,1]
,值域为[0,1]
2.单调不减,若x1<=x2,则F(x1)<=F(x2)
3.离散型的随机变量与阶梯型的分布函数对应,连续型的随机变量与绝对连续型的分布函数对应
2.1.3 概率分布与分布律
设离散型的随机变量X取值为xi(i=1,2,3,....),且各个取值的概率是
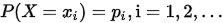
称上式为离散型随机变量X的概率分布或分布律。
特点:
1.非负性 pi>=0 (i=1,2...)
2.规范性 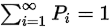
分布律与分布函数
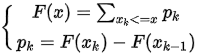
2.1.4 概率密度函数与概率密度
对随机变量X的分布函数F(x),若存在一个非负函数f(x),使得对于任意实数x,有
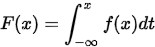
则称函数f(x)为X的概率密度函数,简称概率密度或密度函数。
特点:
1.非负性 f(x)>=0 (i=1,2...)
2.规范性 
分布函数与概率密度
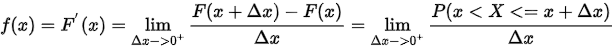
当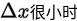
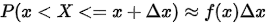
注:f(x)本身不是概率,其大小决定了X落在区间 上的概率,即f(x)反映了点x附近分布的概率
上的概率,即f(x)反映了点x附近分布的概率 疏密 程度(即概率密度)。
累积分布函数
随机变量的取值落在某个区域之内的概率则为概率密度函数在这个区域上的积分
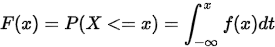
各名词之间的关系
各个名词文字上就差几个字,意思就差别很大了,这也是为什么很多人混淆各个名词的含义的原因,看教材也是各种不理解,经过我反复对比,其实就是三个东西,他们的关系如下:

3.随机变量的数字特征
3.1 数学期望
试验中每次可能结果的概率乘以其结果的总和,是最基本的数学特征之一。它反映随机变量平均取值的大小
具有以下特征:
1.试验中每次可能结果的概率乘以其结果的总和,是最基本的数学特征之一。它反映随机变量平均取值的大小
2.期望值是该变量输出值的平均数。期望值并不一定包含于变量的输出值集合里
3.大数定律规定,随着重复次数接近无穷大,数值的算术平均值几乎肯定地收敛于期望值
3.2 方差
衡量随机变量或一组数据时离散程度的度量。
具有以下特征:
1.方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量
2.概率论中方差用来度量随机变量和其数学期望(即均值)之间的偏离程度
3.统计中的方差(样本方差)是每个样本值与全体样本值的平均数之差的平方值的平均数
3.3 变量之间的相关性度量
协方差与相关系数:这两个名词都是用来描述两个随机变量在变化过程中是同方向变化?还是反方向变化?同向或反向程度如何?
协方差
特点:
1.同向变化的,这时协方差就是正的,反向变化的,这时协方差就是负的。
2.从数值来看,协方差的数值越大,两个变量同向程度也就越大。
计算公式:
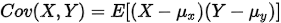
如果有X,Y两个变量,每个时刻的“X值与其均值之差”乘以“Y值与其均值之差”得到一个乘积,再对这每时刻的乘积求和并求出均值.
相关系数
特点:
1.反映两个变量变化时是同向还是反向,如果同向变化就为正,反向变化就为负。
2.相关系数不像协方差一样可以在到
间变化,它只能在+1到-1之间变化。
3.越接近1,表明正相关越强,越接近-1,表明负相关越强,越接近0,表明相关性不强。
计算公式:
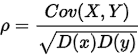
D(x),D(y)为两个随机变量的方差。
相关系数也可以看成协方差:一种剔除了两个变量量纲影响、标准化后的特殊协方差.
协方差矩阵
n维随机变量之间的协方差值,为了方便,用矩阵来组织这些数据,也就是协方差矩阵来
3.4 矩
矩就是观察与描述随机变量的工具,不同的矩就是不同的维度。就是所谓的横看成岭侧成峰,远近高低各不同。通过不同维度的观察,你就能认清你要观察的随机事件的特性了。
零阶矩:所有变量取值的总概率(即1)
一阶矩:期望
二阶矩:随机变量平方后的期望
三阶矩:随机变量三次后的期望,偏斜度
四阶矩:随机变量四次后的期望,峰度
最后放上一张“分布的世界地图”,纯属让大家明白,这东西不是专业人士学不透,后面的文章我也是选一些常见的分布进行讲。

资料:
资料基本摘自百度百科,用标题作为关键字搜索即可,在这不一一列举。
https://www.zhihu.com/question/20852004
https://www.zhihu.com/question/23236070