[poj1024]Tester Program
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 2760 | Accepted: 981 |
Description
Tester Program
For this contest, we first designed the following problem (note that you do not have to solve it!):
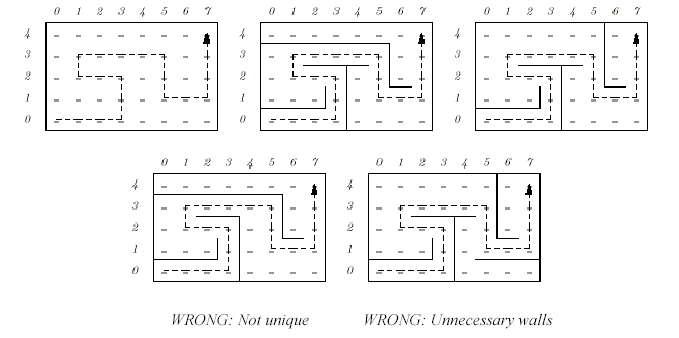
In ACM/ICPC contests, you'll often see questions such as "find the shortest path out of this maze." Let's turn this on its head and ask "given a path, find a maze for which the given path is the shortest path." Our paths will run vertically and horizontally between the regularly spaced points of a rectangular grid. The problem is to compute a set of unit-length baffles (walls) separating grid points that forces the given path to be the unique shortest path from its starting point to the end point. To make things more interesting, we will require that there should be no redundant walls constructed in the sense that it should not be possible to remove any wall and still have the given path as the unique shortest path. In the following figure for example, consider the path through the 8 ? 5 grid on the left maze of the top row. The wall placements in the two mazes to its right (top row) make that path unique. The two mazes on the lower row are faulty.
The path is not unique in the one on the left, and there are some redundant walls on the right.
The first line of the input file contains a single integer t (1 ≤ t ≤ 10), the number of test cases, followed by the input data for each test case. The first line of each test case consists of two integers W and H (1 ≤ W, H ≤ 100) giving the width and height of the grid respectively. The second line of the test case contains a path. The path always starts in the lowerleft corner, (0, 0). It is specified as a string of U (up), D (down), L (left), and R (right) characters (with no embedded white space). You may assume that the path remains within the bounds of the maze and does not intersect itself. It may end anywhere in the maze (i.e., not necessarily in a corner or against a wall).
First line of the output for the i-th test case (starting from one) should contain an integer M, the number of walls used in the solution. Following the first line, there are M lines each containing a wall specification in the form of four consecutive integers corresponding to two pairs of (x, y) coordinates specifying adjacent grid points separated by the wall (0 ≤ x < W and 0 ≤ y < H). Note that the possible output is not unique. There should no blank line in the output.
2
8 5
RRRUULLURRRRDDRRUUU
4 3
RRRUU
19
0 0 0 1
1 0 1 1
2 0 2 1
2 1 3 1
3 0 4 0
3 1 4 1
3 2 4 2
3 2 3 3
2 2 2 3
4 2 4 3
0 3 0 4
1 3 1 4
2 3 2 4
3 3 3 4
4 3 4 4
5 3 5 4
5 3 6 3
5 2 6 2
6 1 6 2
2
2 2 3 2
2 2 2 1
This is the end of the original problem statement! Being lazy, we did not want to spend time to write a tester program for this problem, and decided to have you write this for us!
Write a program that receives both input and output as one input test case, and write as output CORRECT or INCORRECT to indicate whether or not the output is correct.
For this contest, we first designed the following problem (note that you do not have to solve it!):
Another Wall in the Maze
In ACM/ICPC contests, you'll often see questions such as "find the shortest path out of this maze." Let's turn this on its head and ask "given a path, find a maze for which the given path is the shortest path." Our paths will run vertically and horizontally between the regularly spaced points of a rectangular grid. The problem is to compute a set of unit-length baffles (walls) separating grid points that forces the given path to be the unique shortest path from its starting point to the end point. To make things more interesting, we will require that there should be no redundant walls constructed in the sense that it should not be possible to remove any wall and still have the given path as the unique shortest path. In the following figure for example, consider the path through the 8 ? 5 grid on the left maze of the top row. The wall placements in the two mazes to its right (top row) make that path unique. The two mazes on the lower row are faulty.
The path is not unique in the one on the left, and there are some redundant walls on the right.

Input (of the original problem)
The first line of the input file contains a single integer t (1 ≤ t ≤ 10), the number of test cases, followed by the input data for each test case. The first line of each test case consists of two integers W and H (1 ≤ W, H ≤ 100) giving the width and height of the grid respectively. The second line of the test case contains a path. The path always starts in the lowerleft corner, (0, 0). It is specified as a string of U (up), D (down), L (left), and R (right) characters (with no embedded white space). You may assume that the path remains within the bounds of the maze and does not intersect itself. It may end anywhere in the maze (i.e., not necessarily in a corner or against a wall).
Output (of the original problem)
First line of the output for the i-th test case (starting from one) should contain an integer M, the number of walls used in the solution. Following the first line, there are M lines each containing a wall specification in the form of four consecutive integers corresponding to two pairs of (x, y) coordinates specifying adjacent grid points separated by the wall (0 ≤ x < W and 0 ≤ y < H). Note that the possible output is not unique. There should no blank line in the output.
Sample Input (of the original problem)
2
8 5
RRRUULLURRRRDDRRUUU
4 3
RRRUU
Sample Output (of the original problem)
19
0 0 0 1
1 0 1 1
2 0 2 1
2 1 3 1
3 0 4 0
3 1 4 1
3 2 4 2
3 2 3 3
2 2 2 3
4 2 4 3
0 3 0 4
1 3 1 4
2 3 2 4
3 3 3 4
4 3 4 4
5 3 5 4
5 3 6 3
5 2 6 2
6 1 6 2
2
2 2 3 2
2 2 2 1
This is the end of the original problem statement! Being lazy, we did not want to spend time to write a tester program for this problem, and decided to have you write this for us!
Write a program that receives both input and output as one input test case, and write as output CORRECT or INCORRECT to indicate whether or not the output is correct.
Input
You read both input and output of the original problem from the standard input;it has each output just after each case's input of the original problem.
Note that the output of original does not have formatting problems, i.e.,
The number of lines in the output file is correct and is as supposed to be.
There are no leading or trailing white space characters in output lines.
Wall specifications are correct, meaning that the four numbers correctly specify a possible wall within the boundary of the maze.
Note that the output of original does not have formatting problems, i.e.,
The number of lines in the output file is correct and is as supposed to be.
There are no leading or trailing white space characters in output lines.
Wall specifications are correct, meaning that the four numbers correctly specify a possible wall within the boundary of the maze.
Output
Your program should write a single line for each test case of the input containing a single word CORRECT or INCORRECT, indicating the original problem has correctly produced the output for that test case or not.
Sample Input
2 8 5 RRRUULLURRRRDDRRUUU 19 0 0 0 1 1 0 1 1 2 0 2 1 2 1 3 1 3 0 4 0 3 1 4 1 3 2 4 2 3 2 3 3 2 2 2 3 4 2 4 3 0 3 0 4 1 3 1 4 2 3 2 4 3 3 3 4 4 3 4 4 5 3 5 4 5 3 6 3 5 2 6 2 6 1 6 2 4 3 RRRUU 2 2 2 3 2 2 2 2 1
Sample Output
CORRECT INCORRECT
Source
Tehran 2002, First Iran Nationwide Internet Programming Contest
题目大意:给你一个地图,上面有墙,其中x1 y1 x2 y2代表一面墙分割了x1,y1与x2,y2
给你一个序列(终点不固定),请问这是否是唯一的最短的路径,在地图中是否有墙多余? (如果不满足其一输出“INCORRECT“)
试题分析:很好的一道搜索题,将每个点到终点、起点的距离全算出来,然后枚举不在这路径上的点,如果到终点距离+到起点距离<=字符串长度,不是唯一/最优
那么判断多余墙的只需要将这个墙砸掉,如果被墙隔开的两个方块的起点距离+终点距离>字符串长度 且 终点距离+起点距离>字符串长度那么这个墙是废的。
数据discuss中有
代码
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
inline int read(){
int x=0,f=1;char c=getchar();
for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
for(;isdigit(c);c=getchar()) x=x*10+c-'0';
return x*f;
}
int T;
int N,M;
char str[100001];
bool path[101][101];
bool to[101][101][4];//0:up 1:do 2:lf 3:rt
int toed[101][101];
int tobg[101][101];
bool vis[101][101];
int stx,sty;
int W;
int a1[1001],b1[1001],c1[1001],d1[1001];
struct data{
int x,y,st;
}Que[100001];
int dis[5][2]={{1,0},{0,1},{-1,0},{0,-1}};
void BFS(bool k){
int l=1,r=1;
Que[l].x=stx,Que[l].y=sty;
vis[stx][sty]=true;
while(l<=r){
int a=Que[l].x,b=Que[l].y;
//cout<<a<<" "<<b<<":"<<Que[l].st<<endl;
for(int i=0;i<4;i++){
//cout<<to[a][b][i]<<endl;
if(to[a][b][i]){continue;}
int xx=a+dis[i][0];
int yy=b+dis[i][1];
if(xx<0||yy<0||xx>N-1||yy>M-1||vis[xx][yy]) continue;
vis[xx][yy]=true;
if(k==0)toed[xx][yy]=Que[l].st+1;
else tobg[xx][yy]=Que[l].st+1;
Que[++r].st=Que[l].st+1;
Que[r].x=xx,Que[r].y=yy;
}
l++;
}
return ;
}
int main(){
T=read();
while(T--){
N=read(),M=read();
cin>>str;int len=strlen(str);
memset(to,0,sizeof(to));
memset(path,0,sizeof(path));
memset(toed,0,sizeof(toed));
memset(tobg,0,sizeof(tobg));
for(int i=0;i<N;i++)
to[i][0][3]=to[i][M-1][1]=1;
for(int i=0;i<M;i++)
to[0][i][2]=to[N-1][i][0]=1;
stx=0,sty=0;
path[stx][sty]=true;
for(int i=0;i<len;i++){
if(str[i]=='R') stx++;
if(str[i]=='L') stx--;
if(str[i]=='D') sty--;
if(str[i]=='U') sty++;
path[stx][sty]=true;
}
W=read();
for(int i=1;i<=W;i++){
int a=read(),b=read(),c=read(),d=read();
if(b<d){
to[a][b][1]=true;
to[c][d][3]=true;
}
if(b>d){
to[a][b][3]=true;
to[c][d][1]=true;
}
if(a<c){
to[a][b][0]=true;
to[c][d][2]=true;
}
if(a>c){
to[a][b][2]=true;
to[c][d][0]=true;
}
a1[i]=a,b1[i]=b,c1[i]=c,d1[i]=d;
}
memset(vis,0,sizeof(vis));
BFS(0);
memset(vis,0,sizeof(vis));
stx=0,sty=0;
BFS(1);
bool flag=false;
for(int i=0;i<N;i++){
for(int j=0;j<M;j++){
if(!path[i][j]){
if(tobg[i][j]+toed[i][j]<=len){
flag=true;
//break;
}
}
//if(!path[i][j])cout<<i<<" "<<j<<":"<<tobg[i][j]<<" "<<toed[i][j]<<endl;
}
//if(flag) break;
}
if(flag){
puts("INCORRECT");
continue;
}
for(int i=1;i<=W;i++){
if((tobg[a1[i]][b1[i]]+toed[c1[i]][d1[i]]>len)&&(tobg[c1[i]][d1[i]]+toed[a1[i]][b1[i]]>len))
{flag=true;break;}
}
if(flag){
puts("INCORRECT");
continue;
}
puts("CORRECT");
}
}