机器学习技法-神经网络（NNet）

课程地址：https://class.coursera.org/ntumltwo-002

重要！重要！重要~

一、神经网络（NNet）的动机

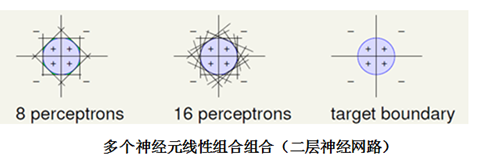
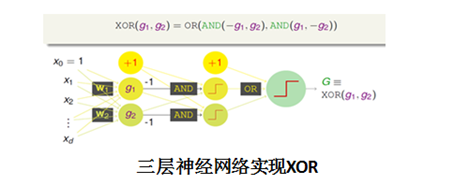
        神经网络有很久的历史，由感知机（perceptron）模型发展而来。单个的perceptron只能处理线性问题，通过组合（融合）多个perceptron，相当于一层的神经网络，能提高perceptron的能力，很容易实现逻辑与、或、非，以及凸集合，但不能实现异或运算。多层次的感知机(perceptrons)模型，不仅能实现异或，功能更为强大。最基本的神经网络也就是一个具有多个层次的perceptron的模型，像飞机借鉴鸟类的飞行一样，神经网络模型借鉴了生物体神经元信息传递的过程。

二、神经网络

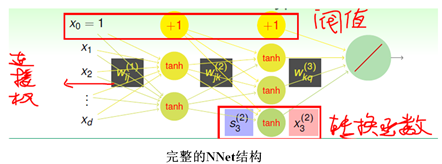
         神经网络是个功能非常强大的模型，输出层可以输出任意范围的数，因此根据需求可以选择分类，回归、以及像LR一样的软分类的任何一种。神经网络中的每一个神经元输入是前一层网络的线性加权的结果，考虑整个网络使用线性模型会使得神经网络能力受限、sign阶梯函数不易优化等的缺点，神经元自身的转换函数选择了与sign阶梯相似的“S”形tanh函数。一个完整的神经网络的设计是比较复杂的，需要确定网络的结构、网络层数、输入、输出、神经元的转换函数、阀值(偏置)、每个连接的权重。林老师在课上将神经网络的物理解释是每一层都通过转换来从数据学习，提取与每一层连接权相匹配的模式，不是很理解/(ㄒoㄒ)/~~

神经网络的属性：

1. 每个神经元的输出，称为该神经元的能量
2. 相邻层神经元节点之间的连接有个权重Wij，其值在[-1,1]之间
3. 除输出层外，每层都会有个阀值，也称为偏置，其值在[0,1]之间
4. 隐藏层之间的每个神经元的输出为该节点输入值的非线性变换(tanh)

三、神经网络的训练和BP算法

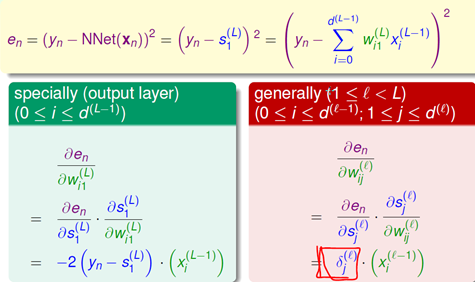
      训练神经网络最常用的是BP（Backpropagation）算法，使用BP算法训练神经网络，实际上就是调整网络的每个神经元的连接权和偏置。BP神经网络分为两部分，前向传输(逐层波浪式的传递输出值)和逆向反馈(反向逐层调整权重和偏置)。BP网络能学习和存储大量的输入-输出模式隐射关系，而无需事前揭示描述这种隐射关系的数学方程。它的学习规则是当实际输出与期望输出不符时，进入误差的反向传播阶段。误差通过输出层，按误差梯度下降的方式修正各层权值，向隐层、输入层逐层反传。周而复始的信息正向传播和误差反向传播过程，使得权值和偏置不断调整，此过程一直进行到网络输出的误差减少到可以接受的程度，或者预先设定的学习次数为止。 下面是数学推导，误差函数为均方误差，对每个连接全的偏导利用链式法则总能由后面的部分推导出来，有兴趣可以参考https://www.zhihu.com/question/27239198

四、神经网络的最优化

      神经网络是个非常复杂的机器学习模型，dvc=O(VD)，V=神经元的数量，D=权重weights的数量。复杂的神经网络虽然功能很强大，但是也会造成过拟合的危险。隐藏层很多的时候，神经网络的解是非凸问题，GD/SGD得到的是局部最优解，很难得到全局解。在工程实践中一般建议会选择比较小的随机的Wij，一般能获得不错的结果。为了防止过拟合，神经网络可以加上之前学过的L1和L2正则化项，为了避免L1不能微分，L2对使得大权重收缩较大，使得小权重收缩较小的缺点，神经网络引入了对大小权重收缩相当的weight-elimination正则化项。除此之外，限制迭代次数，及时停止训练，也能防止过拟合。

参考：http://blog.jobbole.com/90184/

课程地址：https://class.coursera.org/ntumltwo-002