poj2826 An Easy Problem?!【计算几何】

含【三点坐标计算面积】、【判断两线段是否有交点】、【求线段交点】模板

 

An Easy Problem?!

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions:15921		Accepted: 2459

Description

It's raining outside. Farmer Johnson's bull Ben wants some rain to water his flowers. Ben nails two wooden boards on the wall of his barn. Shown in the pictures below, the two boards on the wall just look like two segments on the plane, as they have the same width. 

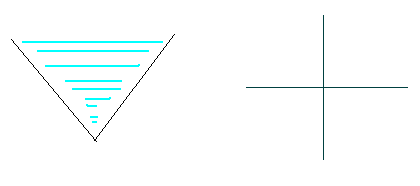
Your mission is to calculate how much rain these two boards can collect. 

Input

The first line contains the number of test cases. 
Each test case consists of 8 integers not exceeding 10,000 by absolute value, x₁, y₁, x₂, y₂, x₃, y₃, x₄, y₄. (x₁, y₁), (x₂, y₂) are the endpoints of one board, and (x₃, y₃), (x₄, y₄) are the endpoints of the other one. 

Output

For each test case output a single line containing a real number with precision up to two decimal places - the amount of rain collected. 

Sample Input

2
0 1 1 0
1 0 2 1

0 1 2 1
1 0 1 2

Sample Output

1.00
0.00

Source

POJ Monthly--2006.04.28, Dagger@PKU_RPWT

题意：

给定四个坐标两条线

现在从上面倒水下来 问这两条线可以接住多少水

思路：

用G++WA了，用C++过了

两条线没有交点的0.00

两条线平行或重合的0.00

需要注意 如果口被封掉的 也是0.00

像这样

之前就在想这样的话需要怎么判断 其实就是如果某条线右边的端点往上找发现被截断了就是口被封住了

之后只需要先求出两线段交点 然后用纵坐标矮一点的那个点水平画线 找到和另一条线的交点

这三个点构成一个三角形 输出其面积

//#include <bits/stdc++.h>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<stdio.h>
#include<cstring>

using namespace std;
typedef long long int LL;

const double eps = 1e-8;

int sgn(double x)
{
    if(fabs(x) < eps) return 0;
    if(x < 0) return -1;
    else return 1;
}
struct point{
    double x, y;
    point(){}
    point(double _x, double _y)
    {
        x = _x;
        y = _y;
    }
    point operator -(const point &b)const
    {
        return point(x - b.x, y - b.y);
    }
    double operator ^(const point &b)const
    {
        return x * b.y - y * b.x;
    }
    double operator *(const point &b)const
    {
        return x * b.x + y * b.y;
    }
    void input()
    {
        scanf("%lf%lf", &x, &y);
    }
};

struct line{
    point s, e;
    line(){}
    line(point _s, point _e)
    {
        s = _s;
        e = _e;
    }
    pair<int, point>operator &(const line &b)const
    {
        point res = s;
        if(sgn((s - e) ^ (b.s - b.e)) == 0){
            if(sgn((s - b.e) ^ (b.s - b.e)) == 0){
                return make_pair(0, res);
            }
            else return make_pair(1, res);
        }
        double t = ((s - b.s) ^ (b.s - b.e)) / ((s - e) ^ (b.s - b.e));
        res.x += (e.x - s.x) * t;
        res.y += (e.y - s.y) * t;
        return make_pair(2, res);
    }
};

bool inter(line l1, line l2)
{
    return
        max(l1.s.x, l1.e.x) >= min(l2.s.x, l2.e.x) &&
        max(l2.s.x, l2.e.x) >= min(l1.s.x, l1.e.x) &&
        max(l1.s.y, l1.e.y) >= min(l2.s.y, l2.e.y) &&
        max(l2.s.y, l2.e.y) >= min(l1.s.y, l1.e.y) &&
        sgn((l2.s - l1.s) ^ (l1.e - l1.s)) * sgn((l2.e - l1.s) ^ (l1.e - l1.s)) <= 0 &&
        sgn((l1.s - l2.s) ^ (l2.e - l1.s)) * sgn((l1.e - l2.s) ^ (l2.e - l2.s)) <= 0;
}

double area(point a, point b, point c)
{
    return fabs((1.0 / 2) * (a.x * (b.y - c.y) + b.x * (c.y - a.y) + c.x * (a.y - b.y)));
}

int t;
line l1, l2;

int main()
{
    scanf("%d", &t);
    while(t--){
        l1.s.input();l1.e.input();
        l2.s.input();l2.e.input();
        if(sgn(l1.s.y - l1.e.y) < 0){
            swap(l1.s, l1.e);
        }
        if(sgn(l2.s.y - l2.e.y) < 0){
            swap(l2.s, l2.e);
        }
        if(!inter(l1, l2)){
            printf("0.00
");
        }
        else if(inter(line(l1.s, point(l1.s.x, 100000)), l2)){
            printf("0.00
");
        }
        else if(inter(line(l2.s, point(l2.s.x, 100000)), l1)){
            printf("0.00
");
        }
        else{
            pair<int, point>pr = l1 & l2;
            if(pr.first != 2){
                printf("0.00
");
            }
            else{
                point a, b;
                if(l1.s.y > l1.e.y){
                    a = l1.s;
                }
                else{
                    a = l1.e;
                }
                if(l2.s.y > l2.e.y){
                    b = l2.s;
                }
                else{
                    b = l2.e;
                }
                if(a.y < b.y){
                    b.x = a.x + 1;b.y = a.y;
                    line l3 = line(a, b);
                    pair<int, point>ppr = l2 & l3;
                    b = ppr.second;
                }
                else{
                    a.x = b.x + 1; a.y = b.y;
                    line l3 = line(a, b);
                    pair<int, point>ppr = l1 & l3;
                    a = ppr.second;
                }
                double ans = area(a, b, pr.second);
                printf("%.2f
", ans);
            }
        }
    }
    return 0;
}