每天两题03

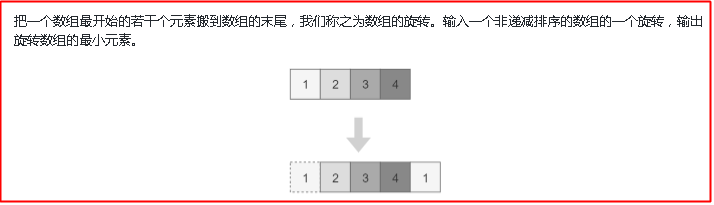
题目一：旋转数组的最小数字

　　思路：说实话看这个题目看了好久题目愣是没看懂，到底是个什么数组啊，又不说清楚，emmm...百度了好久才知道这个数组默认其中的元素的递增的，而且在数组中的元素可能是重复的，比如2344445这种也是行的，我们就分别讨论一下有重复元素和没有重复元素的情况；

　　第一种情况：数组中没有重复元素；

　　顺便提一句，所谓的数组的旋转，就是每次讲第一个元素放到数组的最后一个位置，比如说上面的1234旋转一下是2341，再旋转就是3412，再旋转就是4123,等等，我们可以把这些旋转后的数组叫做原数组的一个旋转

　　不知道大家有没有发现，1234数组的这么多旋转中，如果都从中间进行切分，那么可以看到一半是从小到大进行排序的，另外一半是没有顺序的，而且很明显的是最小的元素始终都是在没有顺序的那一半中，到这里我们可以想到一个很简单的办法，就是每次都将数组且一般，找没有顺序的那个数组，然后对这个没有顺序的数组继续进行同样的切分，直至最后找到最小元素，这种方式也叫做二分法。

　　这里数组不管是奇数还是偶数都一样：

public static int min(int[] arr){
        int left=0;//数组最左边的位置
        int right=arr.length-1;//数组最右边的位置
        
        while (left<right) {
            int midd=(right+left)/2;//数组中间的位置
            if (arr[left]<=arr[midd]) {
                left=midd+1;
            }else{
                right=midd;
            }
        }
        return arr[left];
    }
    
    public static void main(String[] args) {
        int[] arr = {17,1,3,7,9,10};
        int[] arr2 = {5,6,10,17,1};
        System.out.println(min(arr));//1
        System.out.println(min(arr2));//1
    }

　　第二种情况：数组中有重复的元素，我们可以试试，即使数组中有重复的元素，比如原始数组1222334，我们将它进行旋转，2223341,2233412,2334122，其实还是保持着第一种情况中的规律：将数组从中间进行拆分，一半是有顺序的，一半是没有顺序的，注意：这里有一种特殊情况，比如原数组是01111，经过两次旋转之后就是11101，此时从中间切分会发现arr[left] == arr[midd] == arr[right],无法通过比较判断哪边是有顺序的，哪边是没有顺序的；

　　所以如果是这种特殊情况，这里我们就用最简单的遍历去找到其中最小的值就可以了，代码跟上面差不多：

public static int minRotate(int[] arr){
        int left=0;
        int right=arr.length-1;
        while(left<right){
            int midd = (left+right)/2;
            
            //这里就是多了一步处理，其他的代码都是和第一种情况一样的
            if (arr[left] == arr[midd] && arr[midd] == arr[right]) {
                for (int i = left; i < right; i++) {
                    if (arr[i]<arr[i+1]) {
                        return arr[i];
                    }
                }
                return arr[left];
            }else if (arr[midd] <= arr[right]) {
                right = midd;
            }else{
                left = midd+1;
            }
        }
        return arr[left];
    }
    
    public static void main(String[] args) {
        int[] arr = {17,1,3,7,9,10};
        int[] arr2 = {5,6,10,17,1};
        int[] arr3 = {5,5,5,2,5};
        System.out.println(minRotate(arr));//1
        System.out.println(minRotate(arr2));//1
        System.out.println(minRotate(arr3));//2
    }

题目二：剪绳子

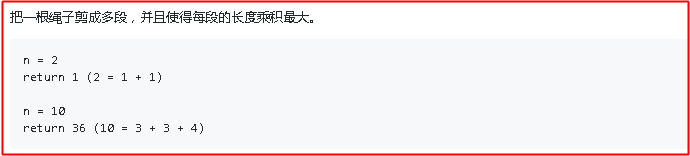
　　 一根长度为n的绳子，剪成多段，每一段都是整数，使得这些整数相乘结果最大；我们可以简单的知道，n=2，最大乘积是1；n=3时，最大乘积是2；n=4时，最大乘积是2x2=4；n=5时，最大乘积是2x3=6。。。

　　那么我们现在要知道，将绳子的每一段尽量剪成多少是最合适的呢？

　　这里比较奇葩，好像是有这么一个规律，当n>=5的时候，对于任意的n，都有这么的一个结论：2(n-2)>n，3(n-3)>n，我们将这两个不等式拆开可以知道就是n>4和n>4.5（可以看到拆开并没什么用），其实我有一个想法，就是首先将长度为n的绳子尽量剪短成长度A，然后再将每一段剪成两段B和C，这两段的乘积BC要大于A，最后算出来的乘积才是最大的！然后根据上面的不等式可以看到，最好的就是剪成的每一段A都可以被2或者3整除，换句话说就是尽量剪成2或者3这个长度的，而且对于同一长度来说，3(n-3)>2(n-2)，最好剪成3，是在不行的话才剪成2（一定不要剪成1，这么不用多说吧。。。如果有个1，那就将3中一个1丢给1，组成2x2）

　　大概就是这么一个逻辑，代码实现：

public static int max(int n){
        if (n<2) {
            return 0;
        }
        if (n==2) {
            return 1;
        }
        if (n==3) {
            return 2;
        }
        //优先计算这个绳子可以拆开为多少个3，假如绳子剪掉了这么多3，余下的长度为1，那么就少剪掉一个3，和1拼成4
        //然后剪成两个2
        int num3 = n/3;
        if((n-num3*3)==1){
            num3--;
        }
        //这里就是计算绳子剪掉了很多的3之后还有多少个2
        int num2 = (n-num3*3)/2;
        //最后就是将这么多的3相乘，所有的2相乘，然后两个结果相乘
        return (int) Math.pow(3, num3)*(int)Math.pow(2, num2);
        
        
    }

    public static void main(String[] args) {
        System.out.println(max(6));//9

    }