1.定义(百度百科)
LASSO是由1996年Robert Tibshirani首次提出,全称Least absolute shrinkage and selection operator。该方法是一种压缩估计。它通过构造一个惩罚函数得到一个较为精炼的模型,使得它压缩一些回归系数,即强制系数绝对值之和小于某个固定值;同时设定一些回归系数为零。因此保留了子集收缩的优点,是一种处理具有复共线性数据的有偏估计。
主要应用于训练数据集较小,但是特征维度较多的时候。
2.筛选特征
当一个模型具有较多特征的时候例如特征包括 (f1,f2,f3,f4),
假设有以上四个特征,这些特征可能起到的作用是不一样的,为了减少计算量,我们需要筛选出主要的特征,即得分较高的特征组合。使用的方法有三种枚举法,贪心算法,正则(目标函数)法
1) 枚举法
这种方式比较容易理解,就是列举出这个集合下的所有子集 {f1} {f2} {f3} {f4}
{f1,f2} {f1,f3} {f1,f4} 等等,然后分别计算每种情况下的得分情况,选出最好的特征集合。
2) 贪心算法
如果采用贪心算法,有两种方式,有从空集增加,或者全集减少。
增加法:依次计算只有一个特征的时候的得分选取最高值例如是{f2},下一步在这个集合的基础上增加一个特征继续计算,找到得分更高的即可加入集合。如果,某一步计算的所有得分,都小于上一步的得分,此时即可停止。
减少法:方法基本和上述一样,开始结果集包括{ f1,f2,f3,f4} ,依次去掉一个特征计算得分,选取最高,且大于上一步得分的结果,如果不存在大于上一步的,则终止。
3) 正则目标函数
这一步采用了正则的方式,优化目标函数,从而选择较好的结果。
3.正则简单介绍
L1 :这个表示 n 个 |w| 相加
L2 :这个表示 n 个|w|² 相加
以上正则的作用主要是用来调整模型,防止出现过拟合的情况。
4.目标函数
当采用L2正则的时候

采用L1正则
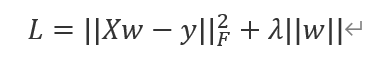
很明显,如果想要求w的最优解,下一步需要对目标函数求导,并令其为0。然后找出最优解w即可。当采用L2正则的时候,正则项求导很容易,但如果是L1
正则的话,求导就要分类讨论了,因为w>0 ,w<0 , w=0时求导结果不同。所以需要采用Coordinate Descent算法来优化Lasso。
5.优化Lasso
优化思想:当特征维度很多的时候,认为只有某一个特征占主要,其他的求导之后为0.
首先先将L拆开
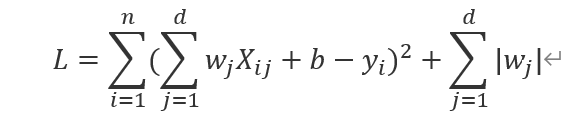
对L求w的偏导
过程如下:
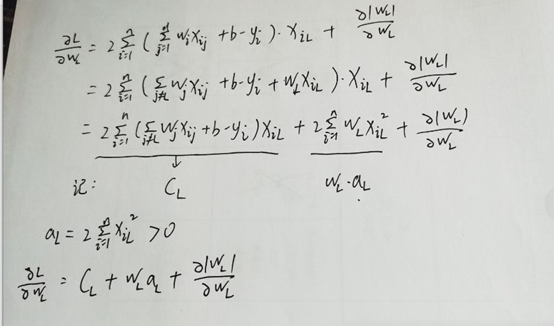
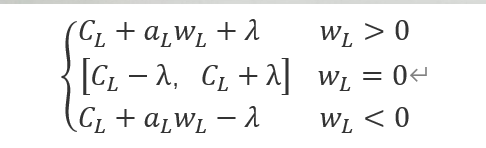
所以可以求出的取值范围


至此基本完成优化。