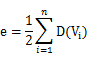数据结构和算法系列-------- 图

原文地址

http://www.cnblogs.com/mcgrady/archive/2013/09/23/3335847.html#_label2

阅读目录

• 一，图的定义
• 二，图相关的概念和术语
• 三，图的创建和遍历
• 四，最小生成树和最短路径
• 五，算法实现

这一篇我们要总结的是图(Graph)，图可能比我们之前学习的线性结构和树形结构都要复杂，不过没有关系，我们一点一点地来总结，那么关于图我想从以下几点进行总结：

1，图的定义？

2，图相关的概念和术语？

3，图的创建和遍历？

4，最小生成树和最短路径？

5，算法实现？

一，图的定义

什么是图呢？

图是一种复杂的非线性结构。

在线性结构中，数据元素之间满足唯一的线性关系，每个数据元素(除第一个和最后一个外)只有一个直接前趋和一个直接后继；

在树形结构中，数据元素之间有着明显的层次关系，并且每个数据元素只与上一层中的一个元素(双亲节点)及下一层的多个元素(孩子节点)相关；

而在图形结构中，节点之间的关系是任意的，图中任意两个数据元素之间都有可能相关。

图G由两个集合V(顶点Vertex)和E(边Edge)组成，定义为G=(V，E)

二，图相关的概念和术语

1，无向图和有向图

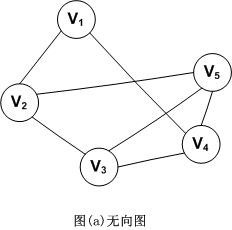
对于一个图，若每条边都是没有方向的，则称该图为无向图。图示如下：

因此，(V_i，V_j)和(V_j，V_i)表示的是同一条边。注意，无向图是用小括号，而下面介绍的有向图是用尖括号。

无向图的顶点集和边集分别表示为：

V(G)={V₁，V₂，V₃，V₄，V₅}

E(G)={(V₁，V₂)，(V₁，V₄)，(V₂，V₃)，(V₂，V₅)，(V₃，V₄)，(V₃，V₅)，(V₄，V₅)}

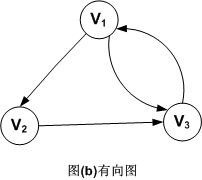
对于一个图G，若每条边都是有方向的，则称该图为有向图。图示如下。

因此，<V_i，V_j>和<V_j，V_i>是两条不同的有向边。注意，有向边又称为弧。

有向图的顶点集和边集分别表示为：

V(G)={V₁，V₂，V₃}

E(G)={<V₁，V₂>，<V₂，V₃>，<V_3，V₁>，<V₁，V₃>}

2，无向完全图和有向完全图

我们将具有n(n-1)/2条边的无向图称为无向完全图。同理，将具有n(n-1)条边的有向图称为有向完全图。

3，顶点的度

对于无向图，顶点的度表示以该顶点作为一个端点的边的数目。比如，图(a)无向图中顶点V₃的度D(V₃)=3

对于有向图，顶点的度分为入度和出度。入度表示以该顶点为终点的入边数目，出度是以该顶点为起点的出边数目，该顶点的度等于其入度和出度之和。比如，顶点V₁的入度ID(V₁)=1，出度OD(V₁)=2，所以D(V₁)=ID(V₁)+OD(V₁)=1+2=3

记住，不管是无向图还是有向图，顶点数n，边数e和顶点的度数有如下关系：

因此，就拿有向图(b)来举例，由公式可以得到图G的边数e=(D(V₁)+D(V₂)+D(V₃))/2=(3+2+3)/2=4

4，子图

故名思义，这个就不解释了。

5，路径，路径长度和回路

路径，比如在无向图G中，存在一个顶点序列V_p,V_i1,V_i2,V_i3…，V_im，V_q，使得(V_p,V_i1)，(V_i1,V_i2)，…,(V_im,V_q)均属于边集E(G)，则称顶点V_p到V_q存在一条路径。

路径长度，是指一条路径上经过的边的数量。

回路，指一条路径的起点和终点为同一个顶点。

6，连通图(无向图)

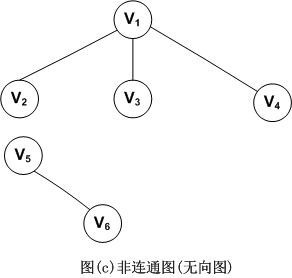
连通图是指图G中任意两个顶点V_i和V_j都连通，则称为连通图。比如图(b)就是连通图。下面是一个非连通图的例子。

上图中，因为V₅和V₆是单独的，所以是非连通图。

7，强连通图(有向图)

强连通图是对于有向图而言的，与无向图的连通图类似。

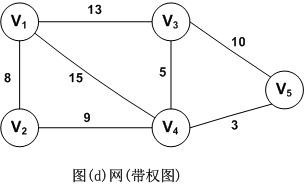
8，网

带”权值”的连通图称为网。如图所示。

三，图的创建和遍历

1，图的两种存储结构

1) 邻接矩阵，原理就是用两个数组，一个数组保存顶点集，一个数组保存边集。下面的算法实现里边我们也是采用这种存储结构。如下图所示：

2) 邻接表，邻接表是图的一种链式存储结构。这种存储结构类似于树的孩子链表。对于图G中每个顶点V_i，把所有邻接于V_i的顶点V_j链成一个单链表，这个单链表称为顶点V_i的邻接表。

2，图的两种遍历方法

1) 深度优先搜索遍历 （这里的解释我没太懂，最起码读第一遍没懂）

深度优先搜索DFS遍历类似于树的前序遍历。其基本思路是：

a) 假设初始状态是图中所有顶点都未曾访问过，则可从图G中任意一顶点v为初始出发点，首先访问出发点v，并将其标记为已访问过。

b) 然后依次从v出发搜索v的每个邻接点w，若w未曾访问过，则以w作为新的出发点出发，继续进行深度优先遍历，直到图中所有和v有路径相通的顶点都被访问到。

c) 若此时图中仍有顶点未被访问，则另选一个未曾访问的顶点作为起点，重复上述步骤，直到图中所有顶点都被访问到为止。

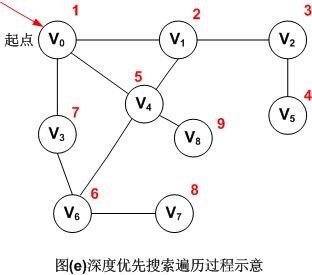
图示如下：

注：红色数字代表遍历的先后顺序，所以图(e)无向图的深度优先遍历的顶点访问序列为：V₀，V₁，V₂，V₅，V₄，V₆，V₃，V₇，V₈

如果采用邻接矩阵存储，则时间复杂度为O(n²)；当采用邻接表时时间复杂度为O(n+e)。

2) 广度优先搜索遍历

广度优先搜索遍历BFS类似于树的按层次遍历。其基本思路是：

a) 首先访问出发点V_i

b) 接着依次访问V_i的所有未被访问过的邻接点V_i1，V_i2，V_i3，…，V_it并均标记为已访问过。

c) 然后再按照V_i1，V_i2，… ，V_it的次序，访问每一个顶点的所有未曾访问过的顶点并均标记为已访问过，依此类推，直到图中所有和初始出发点Vi有路径相通的顶点都被访问过为止。

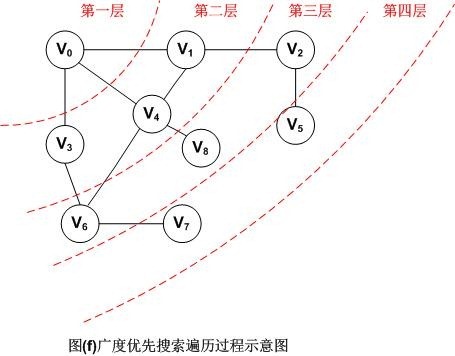
图示如下：

因此，图(f)采用广义优先搜索遍历以V₀为出发点的顶点序列为：V₀，V₁，V₃，V₄，V₂，V₆，V₈，V₅，V₇

如果采用邻接矩阵存储，则时间复杂度为O(n²)，若采用邻接表，则时间复杂度为O(n+e)。

回到顶部

四，最小生成树和最短路径

1，最小生成树

什么是最小生成树呢？在弄清什么是最小生成树之前，我们需要弄清什么是生成树？

用一句语简单概括生成树就是：生成树是将图中所有顶点以最少的边连通的子图。

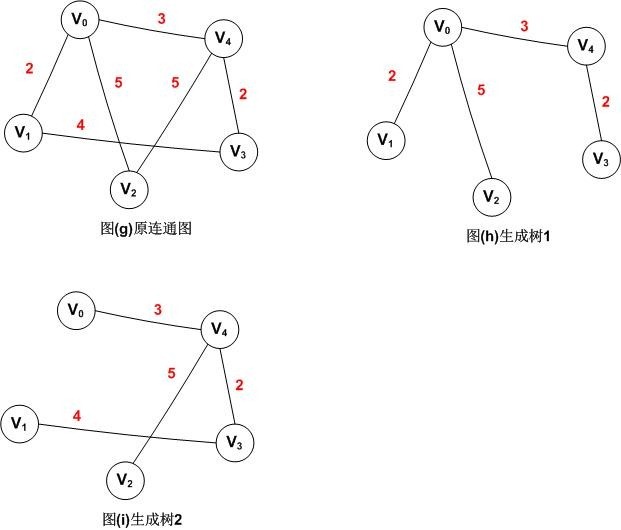
比如图(g)可以同时得到两个生成树图(h)和图(i)

知道了什么是生成树之后，我们就很容易理解什么是最小生成树了。所谓最小生成树，用一句话总结就是：权值和最小的生成树就是最小生成树。

比如上图中的两个生成树，生成树1和生成树2，生成树1的权值和为：12，生成树2的权值为：14，我们可以证明图(h)生成树1就是图(g)的最小生成树。

那么如何构造最小生成树呢？可以使用普里姆算法。

2，最短路径

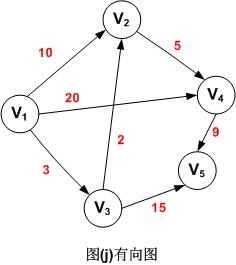
求最短路径也就是求最短路径长度。下面是一个带权值的有向图，表格中分别列出了顶点V1其它各顶点的最短路径长度。

源点	最短路径	终点		路径长度
V1	V1，V3，V2	V2	中转	5
V1	V1，V3	V3	直达	3
V1	V1，V3，V2，V4	V4	中转	10
V1	V1，V3，V5	V5	中转	18

表：顶点V₁到其它各顶点的最短路径表

从图中可以看出，顶点V₁到V₄的路径有3条(V₁，V₂，V₄)，(V₁，V₄)，(V₁，V₃，V₂，V₄)，其路径长度分别为15，20和10，因此，V₁到V₄的最短路径为(V₁，V₃，V₂，V₄)。

那么如何求带权有向图的最短路径长度呢？可以使用迪杰斯特拉(Dijkstra)算法。