题目背景
$frac{1}{4}$遇到了一道水题,叕完全不会做,于是去请教小$D$。小$D$懒得理$frac{1}{4}$,直接就离开了。于是,$frac{1}{4}$只好来问你,这道题是这样的:
题目描述
给定一个无向图,$n$个点(从$1$开始编号)、$m$条边(长度为$1$),每条边有一个权值$c(cin{0,1})$。
一条路径,可以表示为一个长度为经过边数的$01$串,串的第$i$位为经过的第$i$条边的权值。
两条路径相同,当且仅当表示其的$01$串相同。
求从$1$号点出发、长度为$d$的路径种数。
输入格式
从文件$y.in$中读入数据。
第一行,三个整数,$n,m,d$。
接下来$m$行,每行三个整数$u,v,c$,代表一条边连接$u$和$v$,权值为$c$。
输出格式
输出到文件$y.out$中。
输出一行,一个整数,代表答案。
样例
样例输入:
3 2 3
1 2 0
1 3 1
样例输出:
4
数据范围与提示
样例解释:
$1
ightarrow 2
ightarrow 1
ightarrow 2Rightarrow 000$
$1
ightarrow 2
ightarrow 1
ightarrow 3Rightarrow 001$
$1
ightarrow 3
ightarrow 1
ightarrow 2Rightarrow 110$
$1
ightarrow 3
ightarrow 1
ightarrow 3Rightarrow 111$
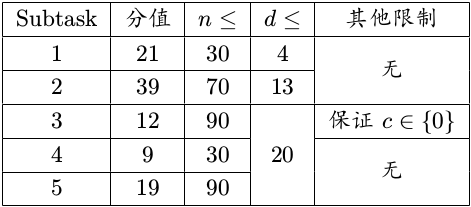
数据范围:
保证$nin [1,90],min [0,n imes (n−1)],din [1,20],u,vin [1,n],cin{0,1}$。
题解
考虑$DP$,设$dp[i][j][stack]$表示从$i$到$j$是否有一条状态为$stack$的连边。
那么显然时间复杂度是:$Theta(s^d imes n imes (n+m))$的。
考虑第一个优化,使用$bitset$,我们能够优化掉$j$那一维。
但是时间复杂度还是不够,于是我们考虑$meet in the middle$算法,只算前一半即可。
时间复杂度:$Theta(2^{frac{d}{2}} imes n imes (n+m)+2^d imes n)$。
期望得分:$100$分。
实际得分:$100$分。
代码时刻
#include<bits/stdc++.h>
using namespace std;
int n,m,d;
bitset<90> bit[4][1100000];
long long ans;
int main()
{
scanf("%d%d%d",&n,&m,&d);
for(int i=1;i<=m;i++)
{
int u,v,c;
scanf("%d%d%d",&u,&v,&c);
if(c)bit[1][u][v]=bit[1][v][u]=1;
else bit[0][u][v]=bit[0][v][u]=1;
}
int dis=(d+1)>>1;
for(int i=n;i;i--)
{
for(int j=0;j<(1<<d);j++)bit[2][j].reset();
bit[2][1][i]=1;
for(int j=1;j<(1<<dis);j++)
for(int k=1;k<=n;k++)
{
if(!bit[2][j][k])continue;
bit[2][j<<1]|=bit[0][k];
bit[2][j<<1|1]|=bit[1][k];
}
for(int j=0;j<(1<<dis);j++)
bit[3][j][i]=bit[2][(1<<dis)|j].count()?1:0;
}
for(int i=0;i<(1<<dis);i++)
for(int j=0;j<(1<<(d-dis));j++)
if(((bit[3][i]&bit[2][(1<<(d-dis))|j]).count()))ans++;
printf("%lld",ans);
return 0;
}
rp++