面试题51：数组中的逆序对（C++）

题目地址：https://leetcode-cn.com/problems/shu-zu-zhong-de-ni-xu-dui-lcof/

题目描述

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。

题目示例

示例 1:

输入: [7,5,6,4]
输出: 5

解题思路

暴力法：最容易想到的是暴力遍历，枚举寻找可能构成逆序对的个数，发现一个则res++，但可惜的是超时。

分治思想：

• Step1：分解，直至剩下一个元素为止，默认长度为1的序列是已经排好序的。

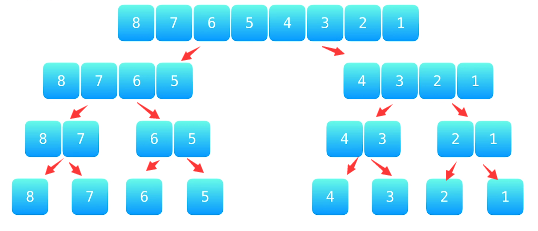
图1

• Step2：合并，自底向上依次合并有序数组，并计算逆序对个数，直至完全合并为有序数组为止。

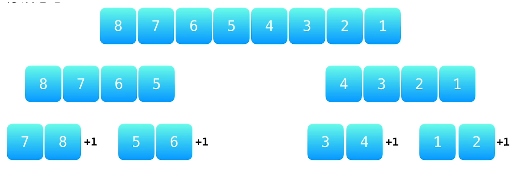
 图2

 图3

图4

归并排序+分治思想：首先，将数组nums拆分为两部分，即nums[left,mid]和nums[mid+1,right]，然后使用递归函数l计算leftPairs和rightPairs两个子序列的逆序对以及归并时的逆序对crossPairs个数，最后返回三者之和leftPairs+rightPairs+crossPairs。当然，归并排序还有可以优化的地方，当我们检测到数组已经有序时，就不需要合并了，直接返回左边和右边逆序对个数即可，即leftPairs+rightPairs。

典型的归并排序实现，其它题目可参考315、327、493.

程序源码

暴力法（超时）

class Solution {
public:
    int reversePairs(vector<int>& nums) {
        if(nums.size() == 0) return 0;
        int res = 0;
        for(int i = 0; i < nums.size() - 1; i++)
        {
            for(int j = i + 1; j < nums.size(); j++)
            {
                if(nums[i] > nums[j])  res++;
            }
        }
        return res;
    }
};

归并排序+分治思想

class Solution {
public:
    int reversePairs(vector<int>& nums) {
        if(nums.size() < 2) return 0; //无法构成逆序对
        int len = nums.size();
        vector<int> copy(len); //拷贝原始数组，因为需要一边计算逆序对的个数，一边排序，因此，算法是修改原始数组的，所以需要拷贝原始数组
        for(int i = 0; i < len; i++)
        {
            copy[i] = nums[i];
        }
        vector<int> temp(len); //辅助数组，归并两个有序数组
        return reversePairs(copy, 0, len - 1, temp); //递归计算逆序对个数
    }
    /*nums[left,right]计算逆序对个数并排序*/
    int reversePairs(vector<int>&nums, int left, int right, vector<int>&temp)
    {
        if(left == right) return 0; //递归终止条件，当left==right时，只剩下一个元素，不构成逆序对
        int mid = left + (right - left) / 2;
        int leftPairs = reversePairs(nums, left, mid, temp);
        int rightPairs = reversePairs(nums, mid + 1, right, temp);
        if(nums[mid] <= nums[mid + 1]) //归并排序优化
        {
            return leftPairs + rightPairs; //若检测到数组已经有序，则不需要合并，直接返回左边和右边逆序对个数即可
        }
        int crossPairs = mergeCount(nums, left, mid, right, temp); //跨越两个区间的逆序对的计算
        return leftPairs + rightPairs + crossPairs; //总逆序对个数
    }
    /*mergetCount()计算前提是nums[left,mid]与nums[mid+1,right]均有序*/
    int mergeCount(vector<int>&nums, int left, int mid, int right, vector<int>&temp)
    {
        //拷贝nums中元素到辅助数组temp中
        for(int i = left; i <= right; i++)
        {
            temp[i] = nums[i];
        }
        int i = left; //i指向区间nums[left,mid]左边界
        int j = mid + 1; //j指向区间nums[mid+1,right]左边界
        int cnt = 0; //计数器
        for(int k = left; k <= right; k++) //确定哪个元素合并到nums中
        {
            if(i == mid + 1) 
            {
                nums[k] == temp[j]; //左指针已经超出区间nums[left,mid]，则直接将nums[mid+1,right]归并到nums数组中
                j++;
            }
            else if(j == right + 1)
            {
                nums[k] = temp[i]; ////右指针已经超出区间nums[mid+1,right]，则直接将nums[left,mid]归并到nums数组中
                i++;
            }
            else{ //左右指针i和j均在区间nums[left,mid]和nums[mid+1,right]中
                 if(temp[i] <= temp[j])
                {
                nums[k] = temp[i];
                i++;
                }
                else
                {
                nums[k] = temp[j];
                j++;
                cnt += (mid - i + 1); //逆序对个数计算，即第一个数组nums[left,mid]中还未归并的元素个数，比如[5,4,3,2,1]和[4，6，7]中，左指针i指向5，右指针j指向4，比较元素5与4，发现5>4，归并元素5到nums数组中，并右指针j++指向元素6，然后计算逆序对的个数4，即[5,4,3,2,1]中还未归并的元素个数(元素4，3，2，1均未归并)
                }
            }
        }
        return cnt;
    }
};

参考文章

https://leetcode-cn.com/problems/shu-zu-zhong-de-ni-xu-dui-lcof/solution/shu-zu-zhong-de-ni-xu-dui-by-leetcode-solution/