绵阳东辰国际test201910.24

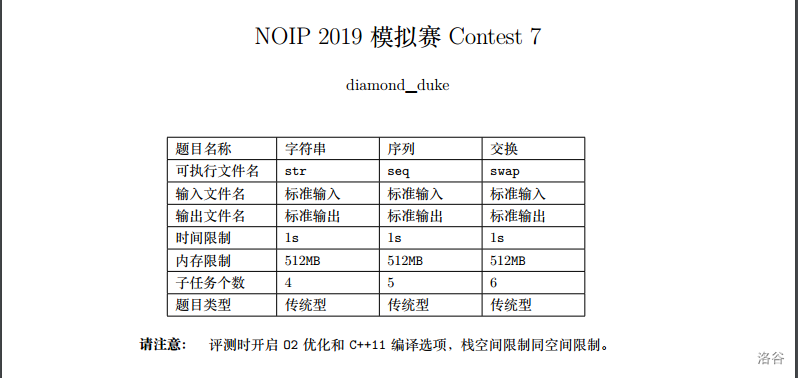
分析：

考虑如何判断一个字符串 S 是不是另一个字符串 T 的子序列。
一个自然的想法是贪心：我们按照从前往后的顺序考虑 S 的每个字母，然后维护
一个 j，表示 S1S2 · · · Si 当前的字符已经匹配到了 T1T2 · · · Tj。然后每次贪心选择下
一个使得 Tj′ = Si+1 的 j′ 匹配过去的

我们考虑 DP 时记录两个序列对应的 j，

那么转移时，预处理出每个字符串每个位置后面第一个 0/1 在哪里即可做到 Θ(1) 转移

nxta[n+1][0]=nxta[n+1][1]=n+1;
	nxtb[m+1][0]=nxtb[m+1][1]=m+1;
	try(i,n,0)
		nxta[i][0]=(a[i+1]=='0'?i+1:nxta[i+1][0]),
		nxta[i][1]=(a[i+1]=='1'?i+1:nxta[i+1][1]);
	try(i,m,0)
		nxtb[i][0]=(b[i+1]=='0'?i+1:nxtb[i+1][0]),
		nxtb[i][1]=(b[i+1]=='1'?i+1:nxtb[i+1][1]);

两个序列是独立的

dp[i,j]------->dp[next[i,0]+1,next[j,0]+1];

​ --------->dp[next[i,1]+1,next[j,1]+1];

+1是为了失配

满足最短的前提是非子序列

所以要从前往后扫

又因为dp是线性的

所以可以在bfs上扫

所以最先到达终点状态的一定最短

又要求字典序最小，则在bfs中先处理0再处理1

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;
#define x first
#define y second
#define mp make_pair
#define pb push_back
#define enum(i,x,y) for(int i=(x);i<=(y);++i)
#define try(i,x,y) for(int i=(x);i>=(y);--i)
void readint(int &x)
{
	x=0;int f=1;char c;
	for(c=getchar();!isdigit(c);c=getchar())if(c=='-')f=-1;
	for(;isdigit(c);c=getchar())x=x*10+c-'0';
	x*=f;
}
inline void chkmin(int &x,int y){x>y?x=y:0;}
inline void chkmax(int &x,int y){x<y?x=y:0;}
const int MAXN=4005,INF=0x3f3f3f3f;

int n,m;
char a[MAXN],b[MAXN];
int nxta[MAXN][2],nxtb[MAXN][2];
pii q[MAXN*MAXN],from[MAXN][MAXN];
bool vis[MAXN][MAXN];
char c[MAXN][MAXN];
char res[MAXN];

int main()
{
	#ifndef ONLINE_JUDGE
    freopen("code.in","r",stdin);
    //freopen("code.out","w",stdout);
	#endif
	readint(n);readint(m);
	scanf("%s%s",a+1,b+1);
	nxta[n+1][0]=nxta[n+1][1]=n+1;
	nxtb[m+1][0]=nxtb[m+1][1]=m+1;
	try(i,n,0)
		nxta[i][0]=(a[i+1]=='0'?i+1:nxta[i+1][0]),
		nxta[i][1]=(a[i+1]=='1'?i+1:nxta[i+1][1]);
	try(i,m,0)
		nxtb[i][0]=(b[i+1]=='0'?i+1:nxtb[i+1][0]),
		nxtb[i][1]=(b[i+1]=='1'?i+1:nxtb[i+1][1]);
	
	int front=1,rear=0;
	q[++rear]=mp(0,0);
	vis[0][0]=1;
	while(front<=rear)
	{
		pii p=q[front++];
		int tx=nxta[p.x][0],ty=nxtb[p.y][0];
		if(!vis[tx][ty])
		{
			vis[tx][ty]=1;
			q[++rear]=mp(tx,ty);
			from[tx][ty]=mp(p.x,p.y);
			c[tx][ty]='0';
		}
		tx=nxta[p.x][1],ty=nxtb[p.y][1];
		if(!vis[tx][ty])
		{
			vis[tx][ty]=1;
			q[++rear]=mp(tx,ty);
			from[tx][ty]=mp(p.x,p.y);
			c[tx][ty]='1';
		}
	}
/*enum(i,0,n+1)
{
	enum(j,0,m+1)
		cerr<<"("<<from[i][j].x<<","<<from[i][j].y<<") ";
	cerr<<endl;
}*/
	
	int cur=0;
	int x=n+1,y=m+1;
	while(x || y)
	{
		res[++cur]=c[x][y];
		pii p=from[x][y];
		x=p.x,y=p.y;
	}
	try(i,cur,1)putchar(res[i]);
	return 0;
}

分析:

考虑如何使f[x]最大化

即每个出现的数次数为(2的k次方-1)

一定会有这样的最优解方案

why？

因为如果二进制下他不是这种形式，

即说明在这其中会有0

去掉0,f的值不会改变，但原数变小了

白嫖？何乐而不为呢？

code：

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
template <typename T>inline T read()
{
    register T sum=0;
    register char cc=getchar();
    int sym=1;
    while(cc!='-'&&(cc>'9'||cc<'0'))cc=getchar();
    if(cc=='-')sym=-1,cc=getchar();
    sum=sum*10+cc-'0';
    cc=getchar();
    while(cc>='0'&&cc<='9')sum=sum*10+cc-'0',cc=getchar();
    return sym*sum;
}
template <typename T>inline T read(T &a)
{
    a=read<T>();
    return a;
}
template <typename T,typename... Others> inline void read(T& a, Others&... b)
{
    a=read(a);
	read(b...);
}
long long T,n,ans;
bool check(long long M)
{
	long long sum=0;
	ans=0;
	int i=0;
	for(long long j=1;M/j>=1;i++,j<<=1)
	{
		int r=M/j,l=M/(j<<1)+1;
		ans+=(i+1)*(r-l+1);
		sum+=((j<<1)-1)*(l+r)*(r-l+1)/2;
	}
	if(sum>=n)return false;
	ans+=(n-sum)/(M+1);
	return true;
}
int main()
{
	T=read<int>();
	for(int i=1;i<=T;i++)
	{
		n=read<long long>();
		long long l=1,r=1e9;
		while(l<=r)
		{
			long long mid=(l+r)>>1;
			if(check(mid))
				l=mid+1;
			else
				r=mid-1;
		}
		check(r);
		printf("%lld
",ans);
	}
    return 0;
}

分析：

考虑从大到小依次放入元素,要形成合法的序列,加入的元素只能放在当前序列的最左边或者最右边.

加入这个元素时产生的贡献是一个类似于逆序对的东西,可以用树状数组求出加在左边,右边分别产生的贡献.

而加在左边还是右边对之后加入的元素的贡献是没有影响的,若后来的元素加在左边,则它总在后来的那个元素右边.

于是就贪心加,左右两边那边贡献更小,就加在哪边.

#include<bits/stdc++.h>
#define lowbit(x) (x&(-x))
using namespace std;
int t[300005],n;
void modify(int pos){for(int i=pos;i<=n;i+=lowbit(i)) t[i]++;}
int query(int pos){
    int res=0;
    for(int i=pos;i;i-=lowbit(i)) res+=t[i];
    return res;
}
vector<int>pos[300005];
int main(){
    scanf("%d",&n);
    for(int i=1,x;i<=n;i++) scanf("%d",&x),pos[x].push_back(i);
    long long ans=0;
    for(int i=n;i>0;i--){
        int l=pos[i].size();
        for(int j=0;j<l;j++) ans+=min(query(pos[i][j]-1),query(n)-query(pos[i][j]));
        for(int j=0;j<l;j++) modify(pos[i][j]);
    }
    cout<<ans;
    return 0;
}