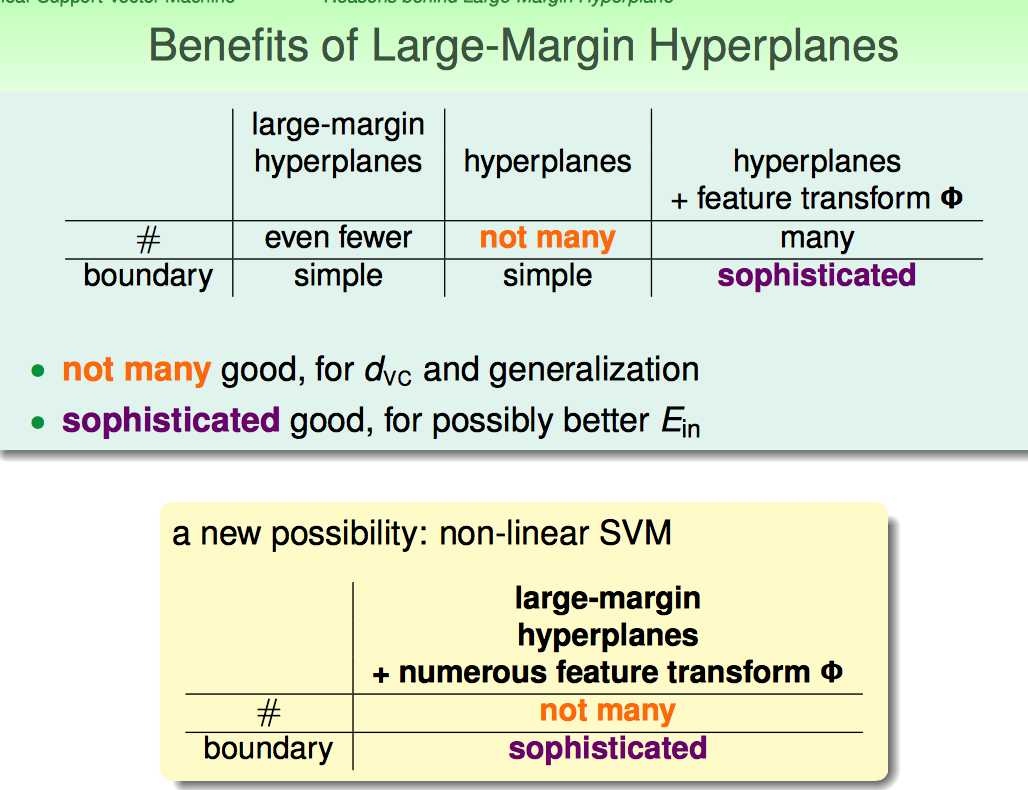
首先从介绍了Large_margin Separating Hyperplane的概念。
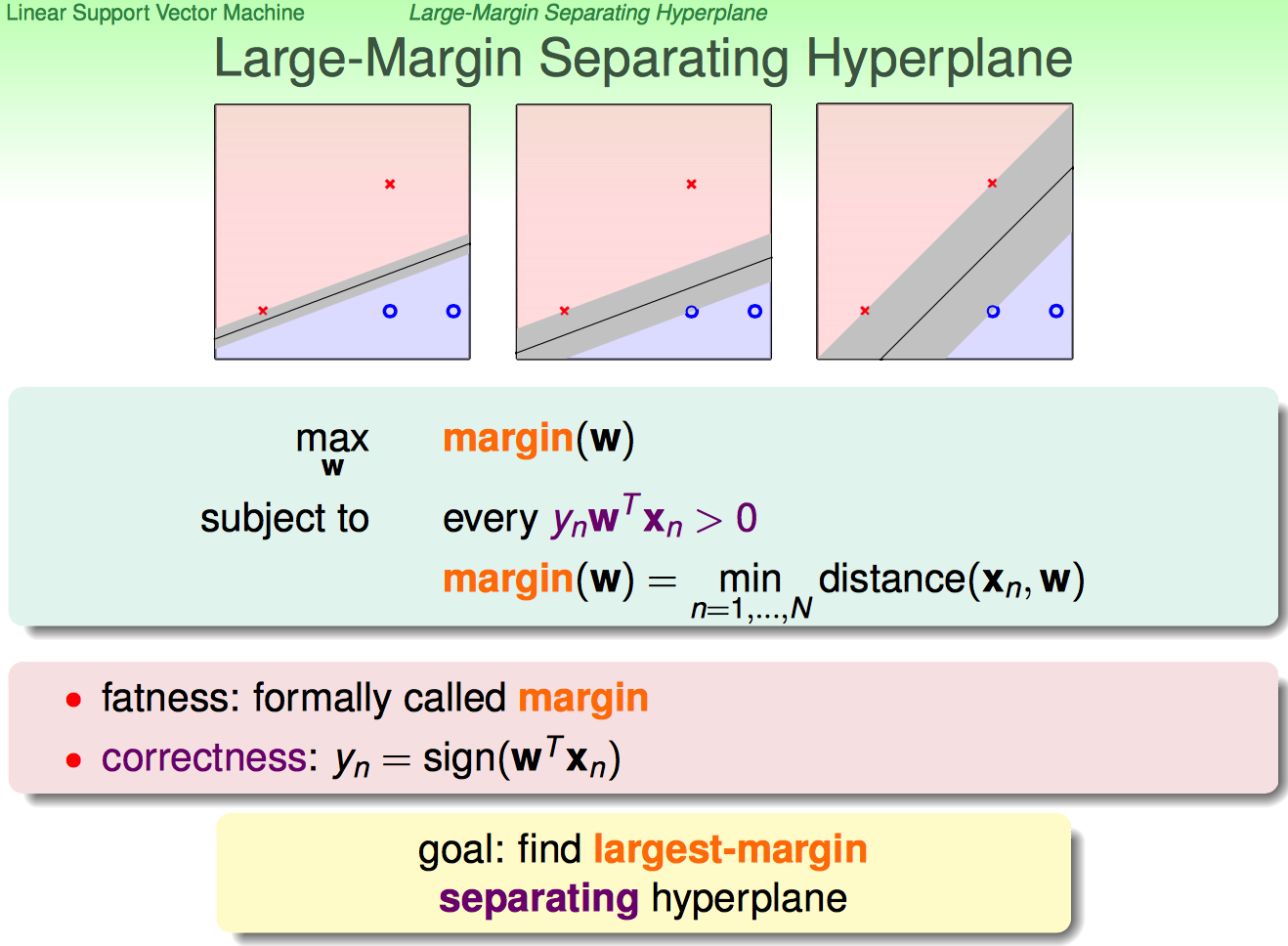
(在linear separable的前提下)找到largest-margin的分界面,即最胖的那条分界线。下面开始一步步说怎么找到largest-margin separating hyperplane。
接下来,林特意强调了变量表示符号的变化,原来的W0换成了b(这样的表示利于推导;觉得这种强调非常负责任,利于学生听懂,要不然符号换来换去的,谁知道你说的是啥)

既然目标是找larger-margin separable hyperplane,那就得先弄明白一个点到平面的距离是啥。
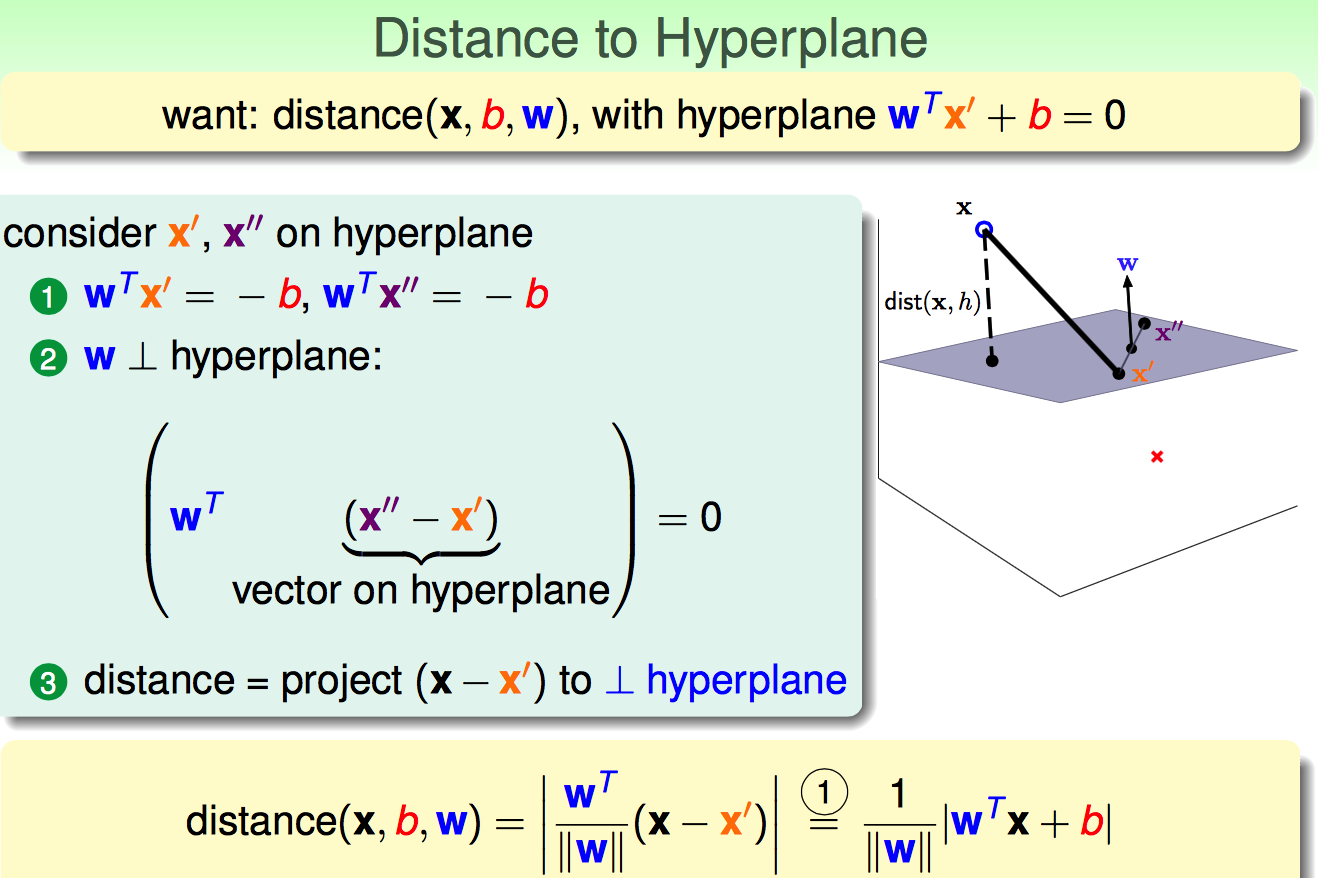
假设x'是平面上的点,x是平面外的点;那么x到平面的距离可以用x-x'再投影到平面法向量w上。
有了点到hyperplane的表达式,就可以把我们需要的larger-margin条件的分类面的求解条件表示出来。

由于假设是数据是linear separable的,所以有yn(W'xn+b)>0。
这时候看subject to部分:
(1)every那条保证了求出的超平面一定是可以分开的
(2)margin那条包含两个意思:
a. 啥叫margin啊?就是离hyperplane最近的点到hyperplane的距离;每个给定的满足条件的hyperplane,都对应一个margin(b,W)
b. 也就是说:一个(b, W)就对应一个hyperplane → 如果hyperplane满足yn(W'xn+b)>0(n=1,...,N)→ 则对应一个margin(b,W)
这样连起来看就捋清晰了:对于某一个separable hyperplane,求margin(b,W)是一个求min的过程;对于所有separable hyperplane产生的margins,求所有margins里面最大的那个margin是一个求max的过程。
截至到上面,larger-margin separable hyperplane的问题就列清楚了。下面开始,就是如何不断简化上约束条件和求解目标。

这里直接从margin的表达式入手,强行指定min yn(W'xn+b)=1 (n=1,...,N);这样margin的表达式就变成了1/||W||这个形式。
我看过的一些资料,对这个的解释就是:对(b,W)放缩大小,使得margin上的点yn(W'xn+b)=1。
上面的说法比较直观,从几何角度规定了这样一个简化方法;但是这种一笔带过的解释并不能使我完全信服,下面从公式的角度解释一下为什么可以做上面的替换。
对于某个hyperplane(b,W)来说,margin是min (1/||W||) * (yn(W'xn+b)),如果直接让yn(W'xn+b)=1,凭什么说1/||W||还是margin呢?
可以这样想:
(1)假设对于某个hyperplane(b,W)来说,margin的值是v(确定的值)→
(2)min (1/||W||) * (yn(W'xn+b)) = v (n=1,...,N) →
(3)min 1/ (||W||/s) * (yn(W'xn/s+b/s)) = v (n=1,...,N) →
(4)令yn(W'xn/s+b/s) = 1 ,再令Wnew = W/s , bnew = b/s →
(5)则有 min (1/||Wnew||) * (yn(Wnew'xn+bnew)) = v (n=1,...,N) →
(6)1/||Wnew|| = v
==================================================
2015-09-09
至于为什么可以放缩w'xn+b,可以从几何角度来理解。以两维输入特征为例:
超平面的方程是:
(1)x1+x2+1:w=[1, 1]' , b=1
(2)10x1+10x2+10:w=[10,10]', b=10
看这两个方程,虽然w和b都不同,但是其实是同一条线。
(1)法向量方向相同,大小不同
(2)直线到(0,0)点的距离都是1/sqrt(2)
==================================================
通过以上6个步骤,令min yn(W’xn+b)=1的背后道理明确了。再进一步简化约束条件,如下:

上面用了一个反证法说明这种替代是可行的。
另外,还有一点需要强点:这里之所以敢把最优化目标函数设定为1/2W'W正是因为,只有当yn(W‘xn+b)=1的时候才能取到最优化的结果。
接下来,用一个例子引出了Support Vector的概念。
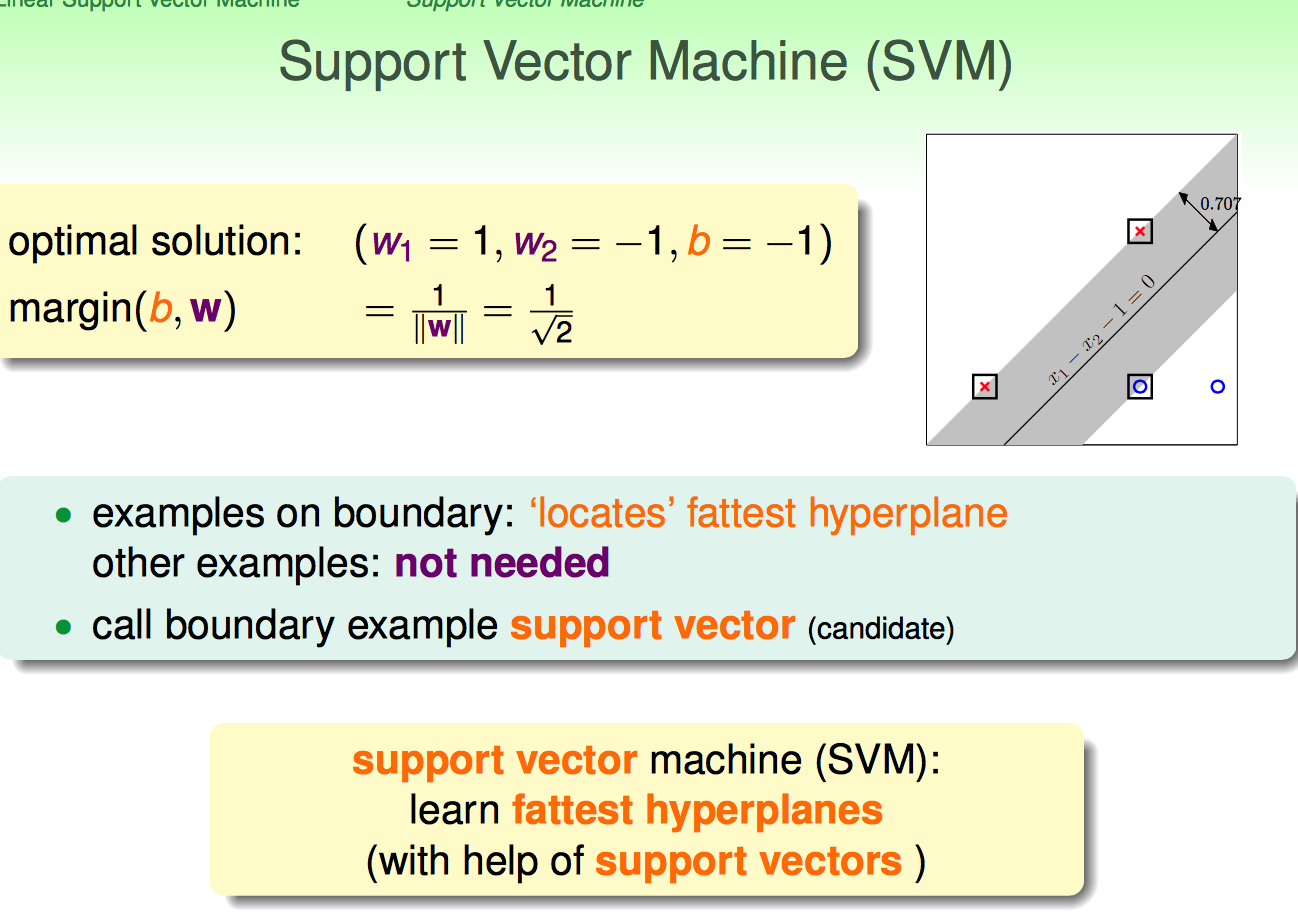
用于hyperplane的这些vector称为support vector。
下面的内容,让我耳目一新。

到上面,突然没有乱七八糟的事情了;林直接说,这是一个典型的quadratic programming(QP)问题;
典型的特点:最优化的表达式是二次的;即这种问题是有常规套路去解的。
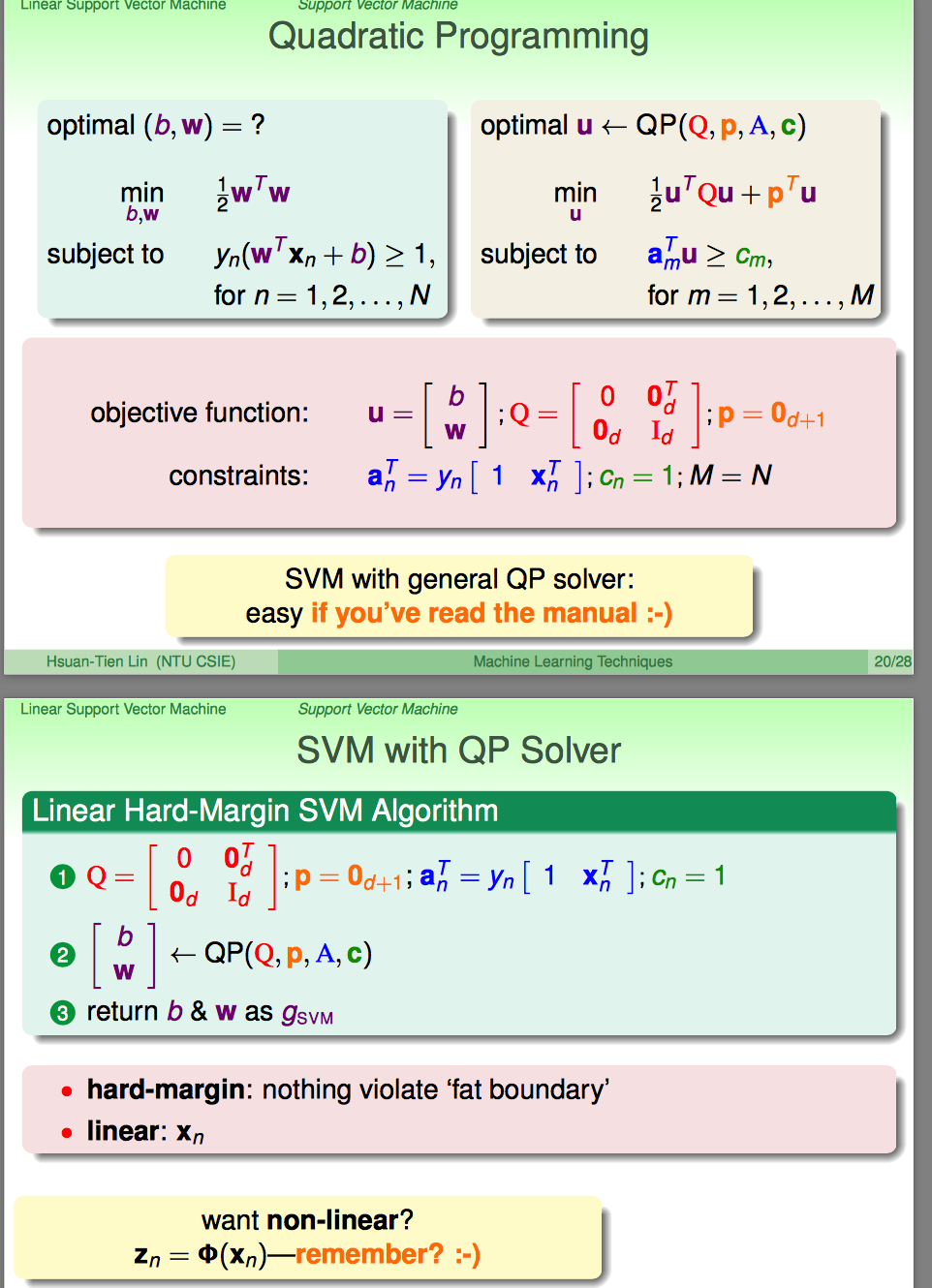
怎么按照QP的常规套路去搞呢?整理出来几个参数就OK了。看到这里,似乎有些傻掉了:说好的KKT那些玩意呢?都不讲了么?
到这里想想也没有啥必要了,都QP直接解出来了,还啥KKT啊。
接下来解释了Large-Margin Hyperplane的背后道理。
Large-Margin控制模型复杂度,控制VC维。

简而言之,Large-Margin的好处就是在带入non-linear transform的情况下,可以控制模型的复杂度。