P2458 [SDOI2006]保安站岗 题解

P2458 [SDOI2006]保安站岗 题解

间隙(原题面)

• 前排声明:蒟蒻刚学OI没多久,讲的可能比较啰嗦,望见谅

大致题意

给一颗树,每个点都可以花费一定的价格来放置一名"保安"

每个保安都可以看管他本身所在的点和所有与他所站的点相邻的点

求:看管所有点所需要的最小花费

分析

树形dp。

先来说一种错误的做法,也是我一开始想到的做法

每个点都有"放置"和"不放置"两种选择

设(dp[i][0])为第(i)个点"不放置"保安所需要的最小花费

(dp[i][1])为第(i)个点“放置”保安所需要的最小花费

如果第(i)个点"放置"了保安

那它的下一个节点则可以选择"放或不放"两种决策

反之,下一个节点必须都"放置"一名保安

很明显是错的

放张图应该就明白了

(下一个节点不一定要由父亲或自己来看管,也可以由自己的"儿子"来看管)

也就是说,每个点的看管对象都有:

• 自己
• 父亲
• 儿子

三种可能

如何转移

设(dp[i][0])为该点由自己看管所产生的最有解

(dp[i][1])为该点由父亲看管所产生的最优解

(dp[i][2])为该点由儿子看管所产生的最优解

• 1.由“自己”看管

自己的位置上已经"放置了"一个点

那么它的所有儿子就都会被自己所"看管"住

显然儿子可以选择任意一种决策

• 得到转移方程:(dp[i][0]=sum min(dp[son][0],dp[son][1],dp[son][2])+w[i])

((w[i])为父亲节点"放置"守卫所需要的价值)

• 2.由“父亲”看管

自己由父亲看管,说明自己所在的点上未"放置"门卫,那儿子肯定只能由自己的儿子看管或由自己看管

• 得到方程:(dp[i][1]=sum min(dp[son][0],dp[son][2]))

• 3.由“儿子”看管

（图中红蓝分别为两种可能情况）

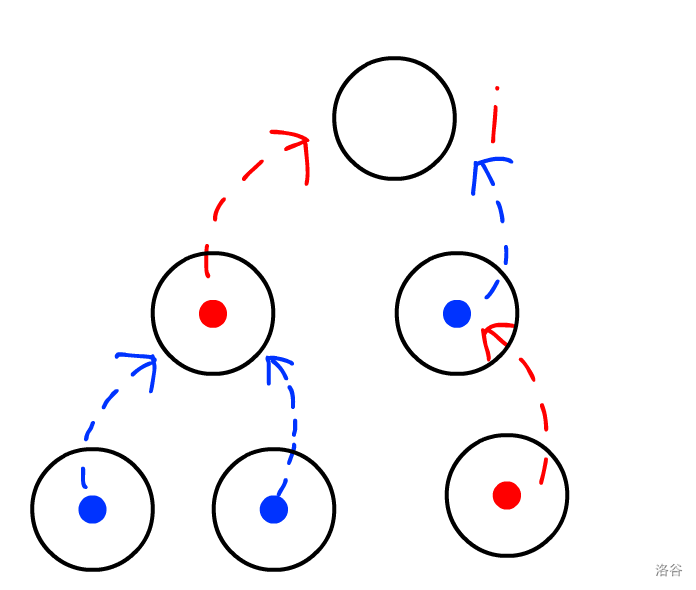
既然是由自己的儿子看管

儿子的决策也有两种可能

1.由儿子的"儿子"看管

2.由自己看管

• 得到方程:(dp[i][2]=sum min(dp[son][2],dp[son][0]))

有一种极端情况,如果全部都选了(dp[son][2])

"自己"就会产生无人看管的情况

因此要在这里加一个小特判,具体代码里有解释

这里做了个简陋的gif,不懂的可以结合代码看一下

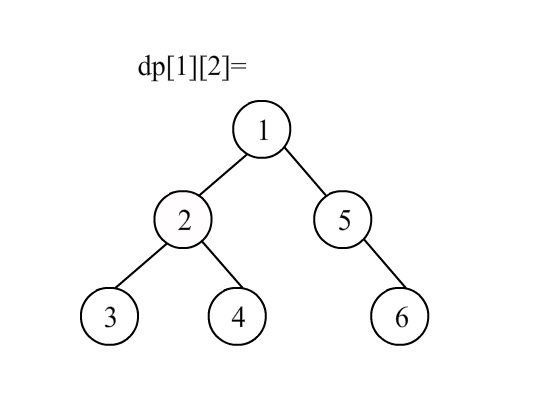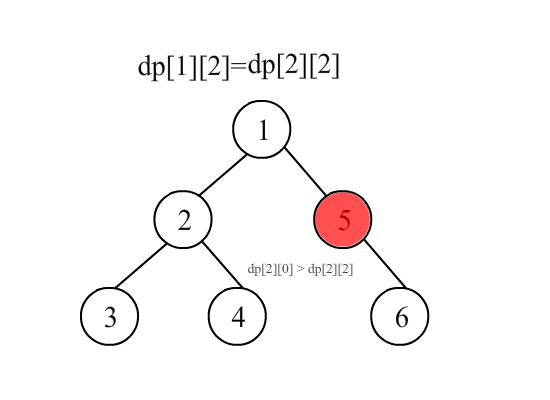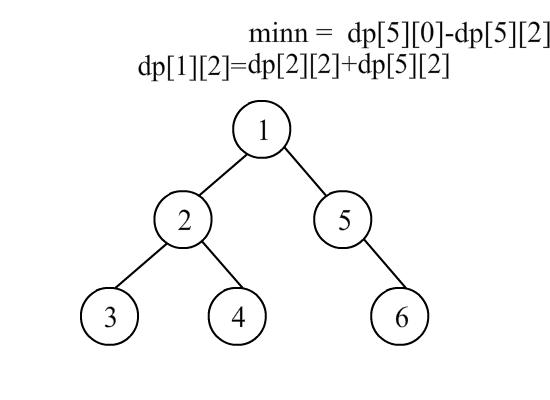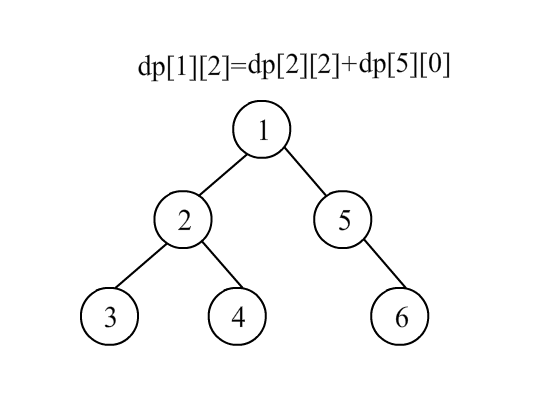
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1510;
int n,dp[MAXN][4],w[MAXN];
int is_head[MAXN];
vector <int> son[MAXN];
void dfs(int x){
	bool is_cs = false;//用来判断有无极端情况
	 
	int minn = 0x3ffffff;//用来求极端情况的最小值 
	dp[x][0] = w[x];
	for(int i=0;i<son[x].size();i++){
		int v = son[x][i];
		dfs(v);
		dp[x][0]+=min(min(dp[v][0],dp[v][1]),dp[v][2]);//由自己看守 
		dp[x][1]+=min(dp[v][2],dp[v][0]);//由父亲看守 
		//由儿子看守 ↓ 
		if(dp[v][0]<dp[v][2]){ 
			dp[x][2]+=dp[v][0];//如果儿子放置守卫花费的钱更少,那就直接在儿子的点上放置一个守卫 
			is_cs=true;//既然儿子的位置上已经放置守卫了,无极端情况存在 
		}
		else{//否则在儿子的儿子上放置守卫 
			minn = min( minn , dp[v][0]-dp[v][2]);//计算最小所需值 
			dp[x][2]+=dp[v][2];
		}
	}
	if(!is_cs) dp[x][2]+=minn;//如果存在极端情况,则加上差值,相当于是消掉dp[-][2],加上dp[-][0] 
}
int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		int u,m;
		scanf("%d%d",&u,&m);
		w[u]=m;
		int k;
		scanf("%d",&k);
		for(int i=1;i<=k;i++){
			int v;
			scanf("%d",&v);
			is_head[v]++;
			son[u].push_back(v);
		}
	}
	for(int i=1;i<=n;i++){
		if(!is_head[i]){
			dfs(i);
			cout<<min(dp[i][0],dp[i][2]);
			return 0;
		}
	}
}