模板
P3373 【模板】线段树 2
设(mtag)为乘法标记,(atag)为加法标记
对于下放后的每一个区间来说,(x=x*mtag+atag*len)(式(1))
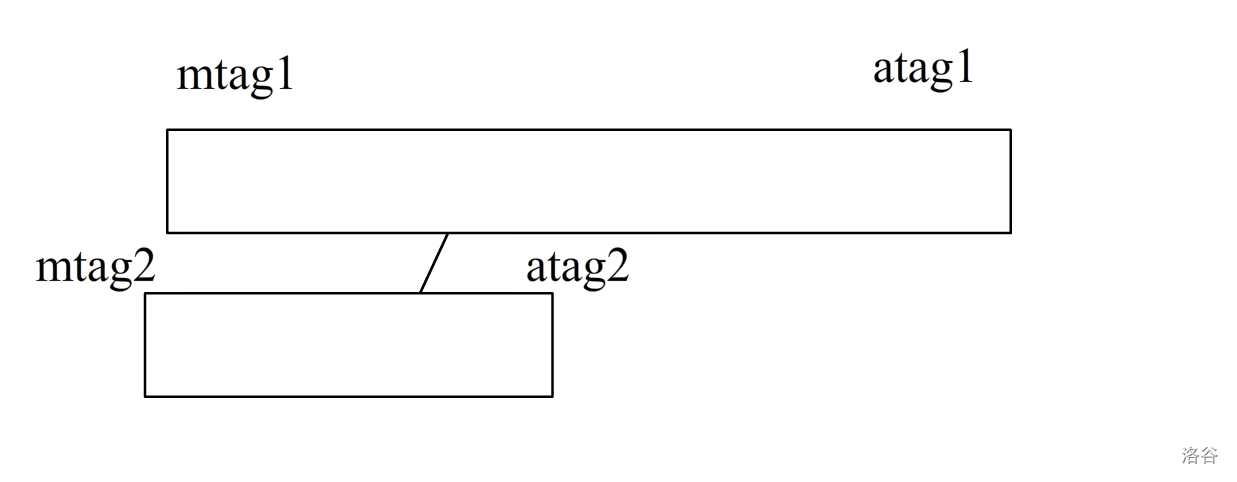
(x=xcdot mtag_2+lencdot atag_2=(xcdot mtag_2+lencdot atag_2)cdot mtag_1+atag_1cdot len)
(=xcdot mtag_2cdot mtag_1+len*atag_2cdot mtag_1+atag_1cdot len)
(=xcdot (mtag_2cdot mtag_1)+lencdot (atag_2cdot mtag_1+atag_1))
再根据前面的式(1),易得
(mtag_2 = mtag_1cdot mtag_2)
(atag_2=atag_2cdot mtag_1+atag_2)
核心(下放)代码:
void pushdown(tree2 *tree,int l,int r){
if(tree->lazym==1&&tree->lazyp==0||tree->lson==NULL) return;
int mid = (l+r)>>1;
tree->lson->x = (tree->lson->x*tree->lazym+(long long)tree->lazyp*(mid-l+1))%mo;
tree->rson->x = (tree->rson->x*tree->lazym+(long long)tree->lazyp*(r-mid))%mo;
tree->lson->lazym = (tree->lazym*tree->lson->lazym)%mo;
tree->rson->lazym = (tree->lazym*tree->rson->lazym)%mo;
tree->lson->lazyp = (tree->lazym*tree->lson->lazyp+tree->lazyp)%mo;
tree->rson->lazyp = (tree->lazym*tree->rson->lazyp+tree->lazyp)%mo;
tree->lazym = 1;
tree->lazyp = 0;
}
基础练习题
P4145 上帝造题的七分钟2 / 花神游历各国
照题里的这个数据范围来看,直接暴力开方肯定会T飞
通过观察,不难发现数据范围内最大的数也只需要(6)次开方就可以变为(1)
考虑剪枝优化:
当一个区间的最大值为(1)时,其整个区间的其他值肯定也为(1)
因此当区间内最大值等于(1)时,直接(return)掉
核心代码:
void change(int node,int l,int r){
int L = tree[node].l,R = tree[node].r;
if(L==R){
tree[node].sum = sqrt(tree[node].sum);
tree[node].maxn = sqrt(tree[node].maxn);
return;
}
int mid = (L+R)>>1;
if(l<=mid&&tree[lson].maxn>1){//最大值大于1时在进行修改操作
change(lson,l,r);
}
if(r>mid&&tree[rson].maxn>1){
change(rson,l,r);
}
pushup(node);
}
P6327 区间加区间sin和
挺好的一道题目,很适合线段树初学者练手
学过和差角公式的应该都能很快想出解法
(sin(a+x) = sinacosx+cosasinx)
(cos(a+x) = cosacosx-sinxsina)
只需要在线段树里维护一个(sinx)和一个(cosx)即可
核心代码:
void update2(int node,double sinv,double cosv){//和差角公式
double cosa = tree[node].cosx;
double sina = tree[node].sinx;
tree[node].cosx = cosa*cosv-sina*sinv;
tree[node].sinx = sina*cosv+cosa*sinv;
return;
}
void pushdown(int node){//下放
if(tree[node].tag){
double cosa = cos(tree[node].tag),sina = sin(tree[node].tag);
update2(lson,sina,cosa);//更新儿子的值
update2(rson,sina,cosa);
tree[lson].tag+=tree[node].tag;//更新儿子的tag
tree[rson].tag+=tree[node].tag;
tree[node].tag = 0;b
}
return;
}
void change(int node,int l,int r,int x){//更新操作
int L = tree[node].l,R = tree[node].r;
if(R<=r&&L>=l){//包围在区间内,直接修改
tree[node].tag+=x;
update2(node,sin(x),cos(x));
return;
}
pushdown(node);//下放
int mid = (L + R)>>1;
if(l<=mid) change(lson,l,r,x);
if(r>mid) change(rson,l,r,x);
update(node);//上传更新
return;
}
P1438 无聊的数列
利用线段树来维护差分数组。
每当进行一个操作(1)时
将点(l)加上首相(k)
如果区间不是一个点的话,则将区间([l+1,r])上的点都加上公差(d)
如果(r<n),则在(r+1)的位置上加上(-(k+(r-l)cdot d))),便于差分
查询时,将区间([1,k])的值都加上即可,相当于查询操作
区间查询,区间修改,直接上线段树模板即可
核心代码:
for(int i=1;i<=m;i++){
int mode,l,r,k,d;
scanf("%d",&mode);
if(mode==1){
scanf("%d%d%d%d",&l,&r,&k,&d);
change(1,1,n,l,l,k);//修改左端点
if(l!=r) change(1,1,n,l+1,r,d);//修改区间
if(r+1<=n) change(1,1,n,r+1,r+1,-(k+(r-l)*d));//修改右端点
}
else{
scanf("%d",&d);
printf("%d
",query(1,1,n,1,d)+a[d]);//差分数组的值+原值
}
}
P4513 小白逛公园
线段树经典题
维护一个从区间左端点开始的区间最大子段(maxl),从右端点开始的区间最大子段(maxr),总区间最大子段(maxx),和一个区间和(sum)
对于(maxl)来说,其右端点的位置有两种可能:
-
在左儿子中
-
在右儿子中
得到方程:(tree.maxl = max(lson.maxl,lson.sum+rson.maxl))
(maxr)也同理
方程:(tree.maxr = max(rson.maxr,rson.sum+lson.maxr))
对于(maxx)来说,其区间范围有三种可能
-
只在左儿子中
-
只在右儿子中
-
既在左儿子中也在右儿子中
得到方程:(tree.maxx = max(lson.maxx,rson.maxx,lson.maxr+rson.maxl)))
查询时只需输出区间([l,r])中的(maxx)即可
核心代码:
更新操作
void update(tree2 *tree,tree2 *lson,tree2 *rson){
tree->sum = lson->sum+rson->sum;
tree->maxl = max(lson->maxl,lson->sum+rson->maxl);
tree->maxr = max(rson->maxr,rson->sum+lson->maxr);
tree->maxX = max(lson->maxX,max(rson->maxX,lson->maxr+rson->maxl));
}
查询操作
tree2 *query(tree2 *tree,int l,int r,int x,int y){
if(x<=l&&y>=r)
return tree;
int mid = (l + r)>>1;
tree2 *t1 = NULL,*t2 = NULL;
if(x<=mid) t1 = query(tree->lson,l,mid,x,y);
if(y>mid) t2 = query(tree->rson,mid+1,r,x,y);
if(t1==NULL) return t2;
if(t2==NULL) return t1;
tree2 *ret = &dizhi[++t];
update(ret,t1,t2);
return ret;
}
P4588 [TJOI2018]数学计算
比较简单的一道题目。
仔细观察不难发现
所谓的操作(1)跟操作(2)其实就是在进行普通的单点修改操作而已
用一个线段树在记录一段区间内的总乘积
操作(1)是把点(i)的值从(1)修改为(i)
操作(2)则是把点(pos)的值修改为(1)
核心代码:
void pushup(int node){
tree[node].val = (tree[lson].val*tree[rson].val)%mo;
}
void build(int node,int l,int r){
if(l==r){
tree[node].val = 1;
return;
}
long long mid = (l + r)>>1;
build(lson,l,mid);
build(rson,mid+1,r);
pushup(node);
}
void change(int node,int l,int r,int x,int y){
if(l==r){
tree[node].val = y;
return;
}
int mid = (l + r)>>1;
if(x<=mid) change(lson,l,mid,x,y);
else change(rson,mid+1,r,x,y);
pushup(node);
}
P2894 [USACO08FEB]Hotel G
跟P4513 小白逛公园大同小异的思路
只是把单点修改操作换成了区间修改罢了
要注意的是这里不存在负值的情况
因此在上传操作时转移没那么复杂,只用判断(maxl)是否等于(sum)
若等于,说明左儿子中房间全为空,直接全部加上,再加上右儿子的(maxl)
若不等于,则为左儿子的(maxl)
(maxr)也同理
同时也要注意这里的查询查的是满足长度为(x)的最左的端点
因此在查询时要满足"能左则左"
核心代码:
void pushup(int node){//上传
if(tree[lson].maxx==tree[lson].sum){//如果左区间全为空房
tree[node].lmax = tree[lson].sum+tree[rson].lmax;//全部加上
}
else{
tree[node].lmax = tree[lson].lmax;
}
if(tree[rson].maxx==tree[rson].sum){
tree[node].rmax = tree[rson].sum+tree[lson].rmax;
}
else{
tree[node].rmax = tree[rson].rmax;
}
tree[node].maxx = max(tree[lson].rmax+tree[rson].lmax,max(tree[lson].maxx,tree[rson].maxx));
}
void build(int node,int l,int r){
tree[node].sum = tree[node].lmax = tree[node].rmax = tree[node].maxx =r-l+1;
if(l==r){
return;
}
build(lson,l,mid);
build(rson,mid+1,r);
}
void pushdown(int node){//下放
if(tree[node].lazy==0) return;
if(tree[node].lazy==1){//退房
tree[lson].maxx = tree[lson].rmax = tree[lson].lmax = 0;
tree[rson].maxx = tree[rson].rmax = tree[rson].lmax = 0;
tree[lson].lazy = tree[rson].lazy = 1;
}
if(tree[node].lazy==2){//开房
tree[lson].maxx = tree[lson].rmax = tree[lson].lmax = tree[lson].sum;
tree[rson].maxx = tree[rson].rmax = tree[rson].lmax = tree[rson].sum;
tree[lson].lazy = tree[rson].lazy = 2;
}
tree[node].lazy = 0;
}
void change(int node,int l,int r,int x,int y,int opt){//opt为1代表退房,为2代表开房
if(x<=l&&y>=r){
if(opt==1) tree[node].maxx = tree[node].lmax = tree[node].rmax = 0;
else tree[node].maxx = tree[node].lmax = tree[node].rmax = tree[node].sum;
tree[node].lazy = opt;
return;
}
pushdown(node);
if(x<=mid) change(lson,l,mid,x,y,opt);
if(y>mid) change(rson,mid+1,r,x,y,opt);
pushup(node);
}
int query(int node,int l,int r,int x){//查询
pushdown(node);
if(l==r) return l;
if(tree[lson].maxx>=x){//如果左区间的最大值大于x,直接查左边
return query(lson,l,mid,x);
}
else if(tree[lson].rmax+tree[rson].lmax>=x){//如果中间大于x
return 1+mid-tree[lson].rmax;左儿子的右最大值,也就是最靠近左边的端点
}
else return query(rson,mid+1,r,x);//否则查右边
}
}
动态开点
CF915E Physical Education Lessons
(now ~ loading...)
扫描线
(now ~ loading...)
``