一、程序结构分析
第一次作业


第一次作业并不难,但感觉对于面对对象不是特别理解,所以很多地方还是沿用了面向过程的方法,将很多过程都放在一个方法里,一个类里,导致尽管作业很简单依然有飘红的点。
第一次的架构很简单,写了一个处理表达式的类,一个正则表达式类,一个项类和表达式类,表达式类用ArrayList容器存储项。第一次作业的性能分也较容易获得,只需考虑合并和开头+号的省略即可。
第二次作业
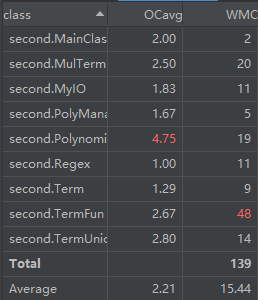
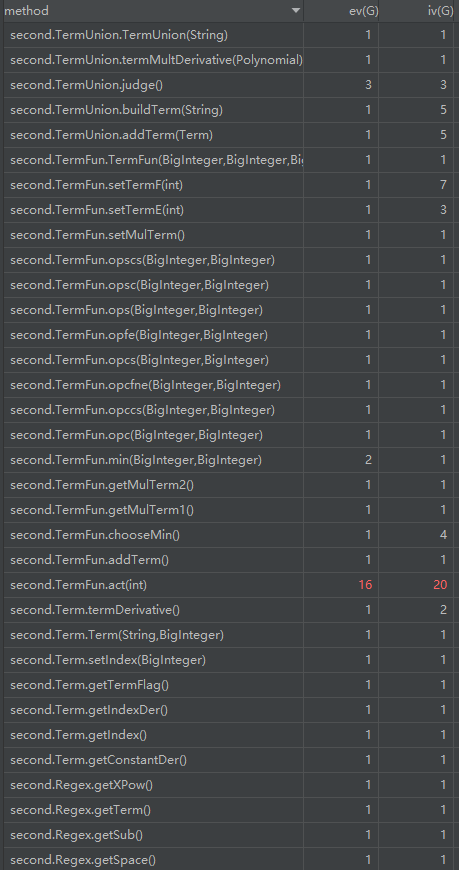
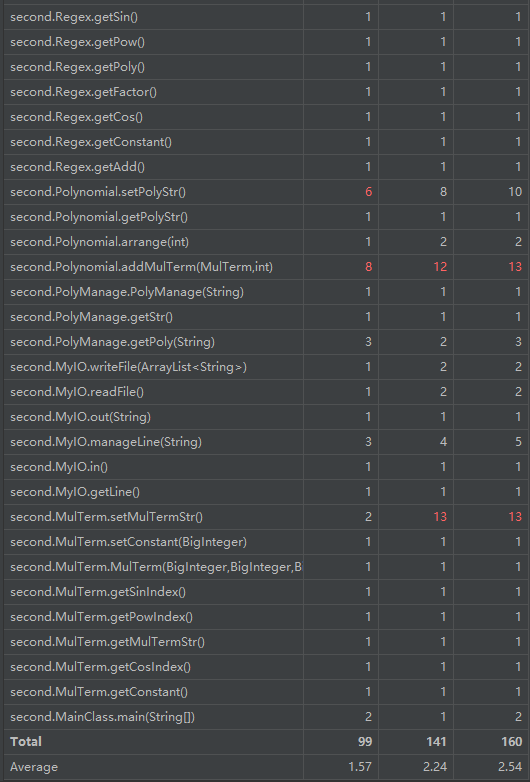

第二次作业相对而言难度就提高了,第一时间都没有思路。第一次作业式只写了一种项,就是带系数的幂函数,第二次作业发现不得不分开,所以分为了常数,cos,sin,幂函数因子,每个项都是这4种因子组合而成,所以专门写了一个TermUnion类专门管理每个由四种因子组合成的项。
这次作业还需要考虑WF,但这次作业的因为不考虑空格的WF,所以直接用正则表达式判断是否符合格式即可。
第二次作业的合并相对困难了很多,因此专门写了一个类TermFun进行项之间的合并,但关于三角函数的最优化简较为复杂,所以我写的方法也很臃肿,但关于三角函数的化简有时候还是无法做到最优。
第三次作业
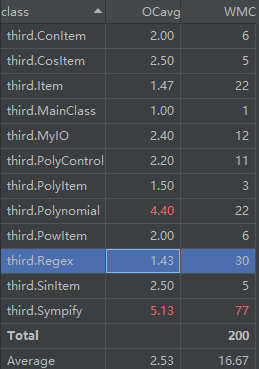


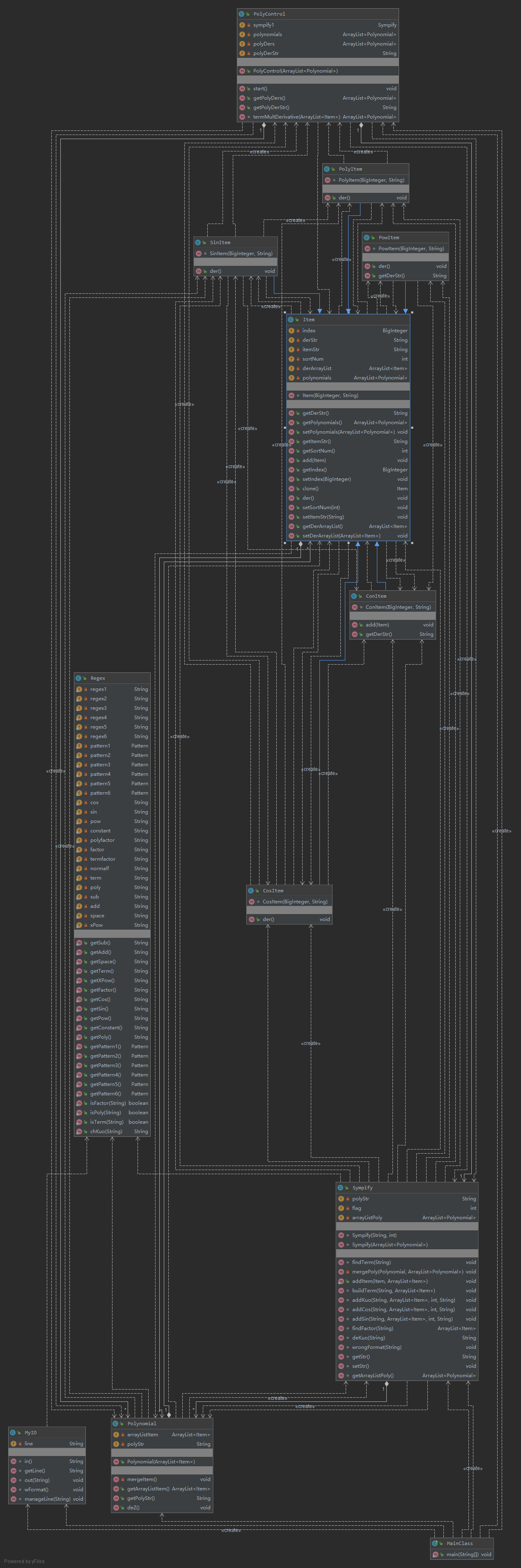
第三次作业难度较高,一开始都不知道如何入手。其实最主要的问题还是前两次作业的构造不适合迭代开发,写法很不成熟,导致第三次作业的工作量大大增加。第三次作业我删去了原来的大部分类,重写了一个Item父类,各种因子都继承自Item类,Item类包含求导方法,求导后结果的字符串形式(cos,sin,还有表达式因子这些可以嵌套的因子中还包含了求导后结果的List形式)。
另外写了一个Sympify类,用来化简表达式同时将表达式转化为List形式,多项式类Polynomial中有方法可以根据多项式的List形式得到其最简的字符串形式。PolyControl类式用来管理多项式的,并含有对整个表达式的求导方法。
所以总体思路就是先将表达式进行去空格的预处理,再通过Sympify类逐层递归得到整个表达式的List形式,然后通过PolyControl类对整个表达式进行求导得到List形式和字符串形式的求导结果,然后输出。
关于WF的处理是再去空格之前进行关于空格WF的判断,然后再逐层递归过程中再进行格式判断。另外关于表达式的合并以及Sympify类写的较为臃肿,复杂度较高,关于代码架构还有很大的优化空间。
二、BUG分析。
第一次作业和第二次作业都没有出现BUG,第三次作业由于大量时间花在了化简上,导致没有全面的对WF进行测试,所以最后强测有三个WF的点没有判出来。互测也有个关于表达式因子的BUG,表达式因子是不能有指数的,而我错误的将两个相同的表达式因子相乘给合并了,导致出现了BUG。这些BUG其实不难发现,主要原因还是由于太过追求性能分导致没有仔细去测试这些细节。
三、互测策略。
主要用评测机进行大规模数据测试,如果有BUG就反馈。第一次作业用评测机没有发现任何BUG,但确实有一位同学的代码是存在BUG的,由于我对指导书的表达式格式的理解不够透彻,导致没有发现这个BUG,第二、第三次都用评测机发现了一些BUG。
对于那些结构清晰的代码,会认真阅读并能从其中学到一些东西,而对于那些结构混乱且没有注释的,还是放弃看了。
很多BUG都是边界数据造成的,所以每次还另外自己写了一些评测机难以随机到的边界数据,用来对自己的程序进行测试和进行互测。
四、应用创建对象模式重构。
这个单元的作业其实都可以用工厂模式来进行对象创建,可以先用正则来匹配出项,再将项的字符串扔给工厂,由工厂内部来构造对应的项,这样既很好的降低了耦合度,也可以让代码结构更加清晰。
五、对比和心得体会。
对于面向对象这一点的认知还是不够清晰,代码的耦合度过高,不符合高内聚低耦合的原则,结构也不是很清晰,类与类之间的关系很混乱。代码的可迭代性太差,每次作业都只考虑到了本次作业的构造,导致下次作业不得不进行大幅度的重构。经过这三次作业,虽然在慢慢的进步,但还是有很多缺陷。不过对于面向对象这一思想总算有了一定的了解,对于以后作业的架构也有了一点想法。在今后的作业中,要充分考虑到可迭代性以及高内聚低耦合的原则。