前言:递归(recursion):递归满足2个条件
1)有反复执行的过程(调用自身)
2)有跳出反复执行过程的条件(递归出口)
第一题:汉诺塔
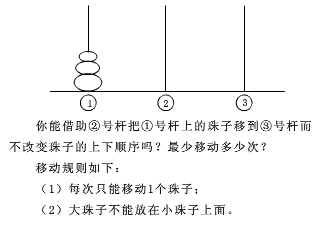
对于这个汉诺塔问题,在写递归时,我们只需要确定两个条件:
1.递归何时结束?
2.递归的核心公式是什么?即:
怎样将n个盘子全部移动到C柱上?
即:若使n个盘子全部移动到C柱上,上一步应该做什么?
代码实现
package diguui;
public class digui1 {
public static void hanoi(int n,int p1,int p2,int p3)
{
if(1==n)
System.out.println("盘子从"+p1+"移到"+p3);
else
{
hanoi(n-1,p1,p3,p2);
System.out.println("盘子从"+p1+"移到"+p3);
hanoi(n-1,p2,p1,p3);
}
}
public static void main(String[] args) {
/*4表示盘数,1表示开始柱子,2表示开始柱子,3表示开始柱子*/
hanoi( 4, 1, 2, 3);
}
}
效果图

第二题:一般而言,兔子在出生两个月后,就有繁殖能力,一对兔子每个月能生出一对小兔子来。如果所有兔子都不死,那么一年以后可以繁殖多少对兔子?
分析如下:
第一个月小兔子没有繁殖能力,所以还是一对;
两个月后,生下一对小兔子,总数共有两对;
三个月以后,老兔子又生下一对,因为小兔子还没有繁殖能力,总数共是三对;
……
依次类推可以列出下表:
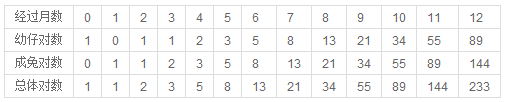
可以得出:
斐波纳契数列,又称黄金分割数列,指的是这样一个数列:1、1、2、3、5、8、13、21、……
这个数列从第三项开始,每一项都等于前两项之和。
package diguui;
public class digui1 {
public static int fun(int m){
if(m<2){
return 1;
}else{
return fun(m - 1)+fun(m-2);
}
}
public static void main(String[] args) {
System.out.println(fun(12));
}
}


