线性支持向量机（2）

拉格朗日对偶问题的转换可以参考：https://www.cnblogs.com/90zeng/p/Lagrange_duality.html

拉格朗日函数泛化的KKT条件而得出的求解函数极大极小问题，可参考：https://www.cnblogs.com/zhangchaoyang/articles/2726873.html

为了求解线性可分支持向量机的最优化问题，将它作为原始最优化问题，应用拉格朗日对偶性，通过求解对偶性问题得到原始问题的最优解，这就是线性可分支持向量机的对偶算法。主要原因在于对偶问题更容易求解，且自然引入核函数，进一步推广到非线性分类问题。

首先构建拉格朗日函数，为此对每一个不等式约束引进拉格朗日乘子,定义拉格朗日函数：

其中a=(a₁,a₂,....,a_N)^T为拉格朗日乘子向量。根据拉格朗日对偶性，原始问题的对偶性是极大极小问题：

所以为了得到对偶问题的解，需要先求L(w,b,a)对w，b的极小，再求对a的极大。

(1) 求

将拉格朗日函数L(w,b,a)分别对w,b求偏导数并令其等于0。

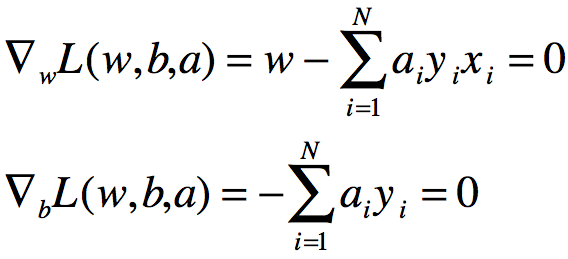
得：

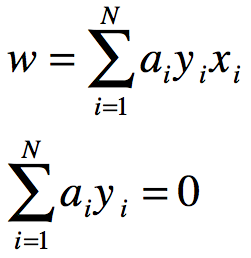
 将上式得到的w值代入拉格朗日函数，可得：

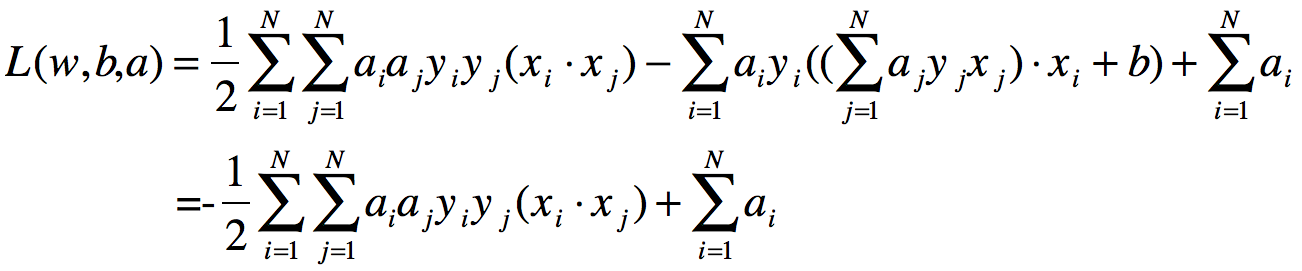
即：

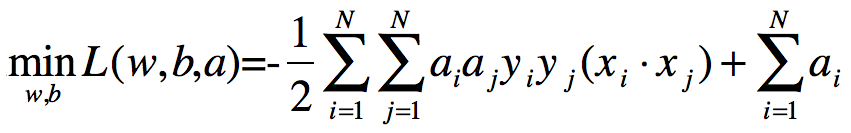
求对a的极大，即是对偶问题：

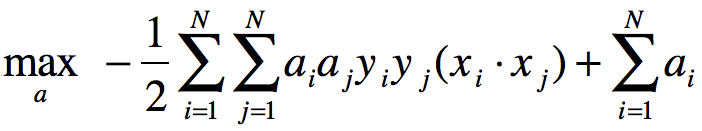
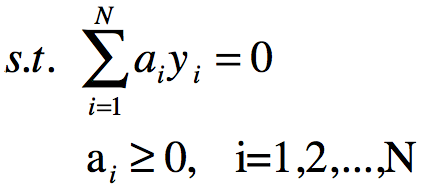
将上式的目标函数由求极大转为求极小，就得到下面与之等价的对偶最优化问题：

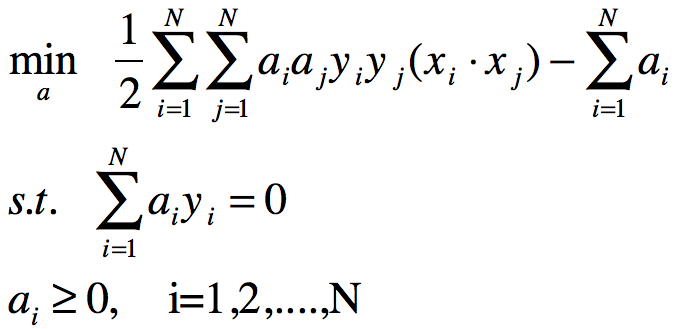
对线性可分训练数据集，假设对偶最优化问题对拉格朗日乘子向量a的解为，可以由a^*求得原始最优化问题对(w,b)的解w^*,b^*.

定理：设a^*是对偶最优化问题的解，则存在下标j，使得，并可按下式求得原始最优化问题的解w^*,b^*(书上并未给出下式中j的含义，本人的理解为j为求得最优化问题的解a^*后，通过其大于0的样本点作为j的样本点，并代入b^*中，并且该部分求得的b^*一致):

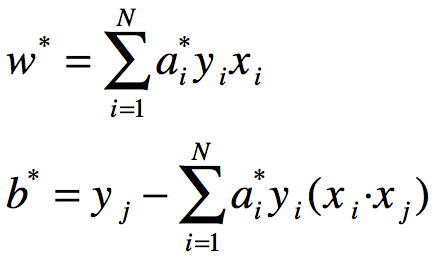
由上定理可求得分离超平面：

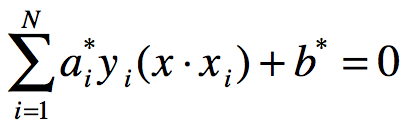
分类决策函数可以写成：

也就是说分类决策函数只依赖于输入x和训练样本输入的内积，上式称为线性可分支持向量机的对偶形式。

综上，对给定线性可分训练集，可首先求对偶问题的解a^*，再通过如上定理求得原始问题的解w^*,b^*,从而得到分离超平面及分类决策函数，这种算法称为线性可分支持向量机的对偶学习算法。

线性可分支持向量机算法如下：

输入：线性可分训练集T={(x₁,y₁),(x₂,y₂),...(x_n,y_n)},其中

输出：分离超平面和分离决策函数

(1) 构造并求解约束最优化问题

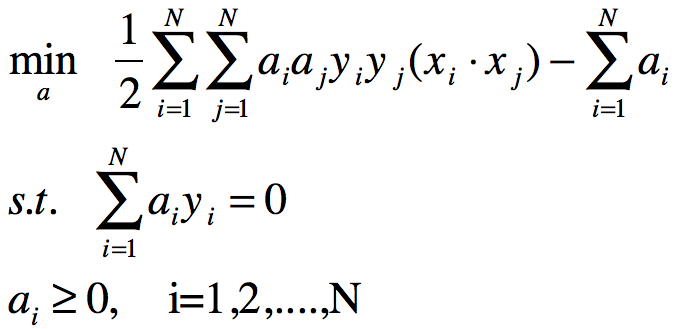
求得最优解

 (2) 计算

 

选择a^*的一个正分量,计算

(3) 求得分离超平面:

w^*x+b^*=0

分类决策函数：

f(x)=sign(w^*x+b^*)

在线性可分支持向量机中，由上算法可以发现，w^*和b^*只依赖于训练数据中对应于a^*>0的样本点(x_i,y_i)，而其他样本点对w^*和b^*没有影响，我们将训练数据中对应于的实例点x_i称为支持向量。