树状数组与线段树（三）

找规律题

1.螺旋折线

如下图所示的螺旋折线经过平面上所有整点恰好一次。

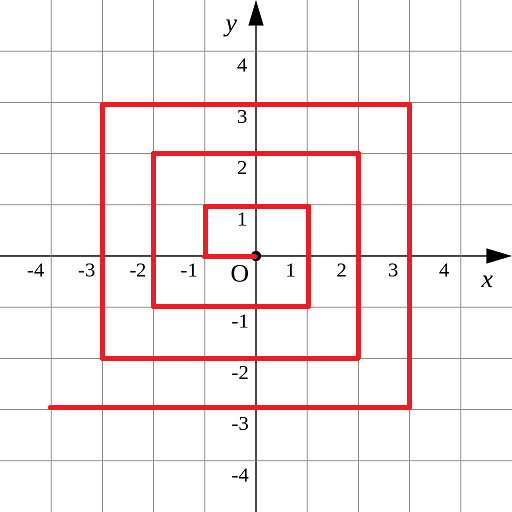
对于整点 (X,Y)，我们定义它到原点的距离 dis(X,Y) 是从原点到 (X,Y) 的螺旋折线段的长度。

例如 dis(0,1)=3,dis(−2,−1)=9

给出整点坐标 (X,Y)，你能计算出 dis(X,Y)吗？

输入格式

包含两个整数 X,Y。

输出格式

输出一个整数，表示 dis(X,Y)。

数据范围

−10⁹≤X,Y≤10⁹

输入样例：

0 1

输出样例：

3
解题思路：这是一道找规律题，我们可以将整个坐标都用距离标识一下，如下图

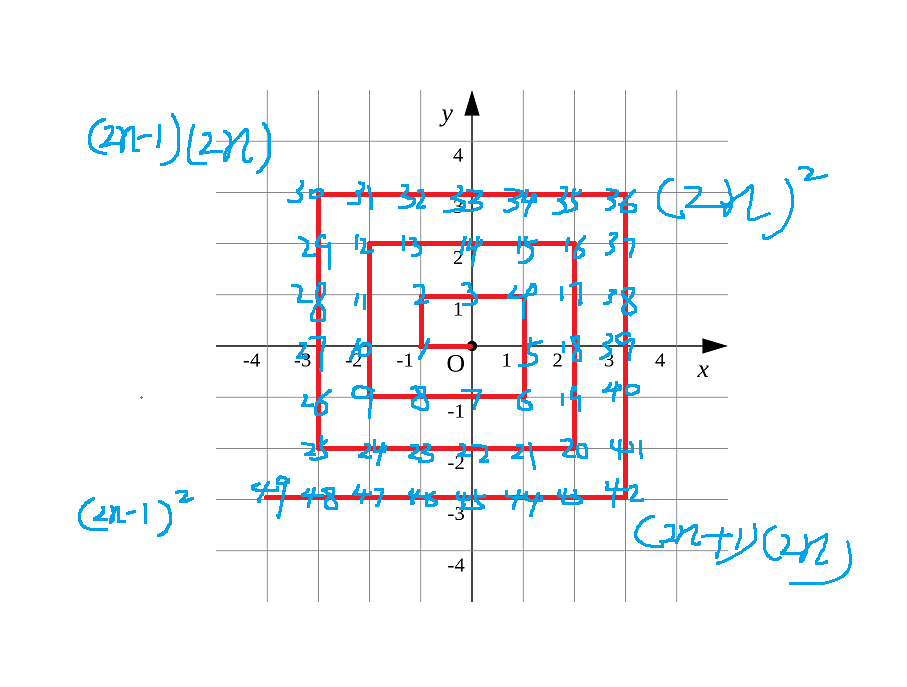
 我们先看x>=0&&y>=0时：若x>=y,dis=(2*x)*(2*x)+(x-y),若x<y,dis=(2*y)*(2*y)-(y-x)

再看x<0&&y>0:x取绝对值，若x>=y,dis=(2*x-1)*(2*x)-(x-y)，若x<y,dis=(2*y-1)*(2*y)+(y-x)

再看x<=0&&y<=0：x取绝对值，y取绝对值，若x>=y&&x!=0&&y!=0,dis=(2*x-1)*(2*x-1)+(x-y),若x<y&&x!=0&&y!=0，dis=(2*y+1)*(2*y+1)-(y+1-x)

其中需要特殊考虑x和y的负半轴，x!=0&&y==0，dis=(2*x-1)*(2*x-1)+(x-1)，当x==0&&y!=0，dis=(2*y+1)*(2*y+1)-(y+1)

再看x>0&&y<0时：y取绝对值，当x<=y，dis=(2*y+1)*(2*y)+(y-x)，当x>y时，dis=(2*x+1)*(2*x)-(x-y)

代码：

#include<iostream>
using namespace std;
typedef long long ll;
int main()
{
    ll x,y,i,j;
    cin>>x>>y;
    if(x>=0&&y>=0)
    {
        if(y>=x)
            cout<<(2*y)*(2*y)-(y-x)<<endl;
        else if(y<x)
            cout<<(2*x)*(2*x)+(x-y)<<endl;
    }
    else if(x<0&&y>0)
    {
        x=-x;
        if(x>=y)
            cout<<(2*x-1)*(2*x)-(x-y)<<endl;
        else if(x<y)
            cout<<(2*y-1)*(2*y)+(y-x)<<endl;
    }
    else if(x<=0&&y<=0)
    {
        x=-x;y=-y;
        if(x>=y&&x!=0&&y!=0)
        {
            cout<<(2*x-1)*(2*x-1)+(x-y)<<endl;
        }
        else if(x<y&&x!=0&&y!=0)
            cout<<(2*y+1)*(2*y+1)-(y+1-x)<<endl;
        else if(x!=0&&y==0)
            cout<<(2*x-1)*(2*x-1)+(x-1)<<endl;
        else if(x==0&&y!=0)
            cout<<(2*y+1)*(2*y+1)-(y+1)<<endl;
    }
    else if(x>0&&y<0)
    {
        y=-y;
        if(x<=y)
            cout<<(2*y+1)*(2*y)+(y-x)<<endl;
        else if(x>y)
            cout<<(2*x+1)*(2*x)-(x-y)<<endl;
    }
    return 0;
}

（二）差分

1.差分矩阵

输入一个n行m列的整数矩阵，再输入q个操作，每个操作包含五个整数x1, y1, x2, y2, c，其中(x1, y1)和(x2, y2)表示一个子矩阵的左上角坐标和右下角坐标。

每个操作都要将选中的子矩阵中的每个元素的值加上c。

请你将进行完所有操作后的矩阵输出。

输入格式

第一行包含整数n,m,q。

接下来n行，每行包含m个整数，表示整数矩阵。

接下来q行，每行包含5个整数x1, y1, x2, y2, c，表示一个操作。

输出格式

共 n 行，每行 m 个整数，表示所有操作进行完毕后的最终矩阵。

数据范围

1≤n,m≤1000
1≤q≤100000
1≤x1≤x2≤n
1≤y1≤y2≤m
−1000≤c≤1000
−1000≤矩阵内元素的值≤1000

输入样例：

3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1

输出样例：

2 3 4 1
4 3 4 1
2 2 2 2

解题思路：差分矩阵是二维的，之前的差分数组是一维的，他的解题思路与一维的思路是一样的
核心：a[N][N],b[N][N]，a数组是b数组的前缀和
因此要在（x1,y1）,（x2,y2）之间加上一个数，则需要将

b[x1][y1]+=c;
b[x1][y2+1]-=c;
b[x2+1][y1]-=c;
b[x2+1][y2+1]+=c;

这样才能满足差分矩阵的要求

代码：

#include<iostream>
#include<cstdio>
using namespace std;
const int N=1010;
int n,m,q;
int a[N][N],b[N][N];

void insert(int x1,int y1,int x2,int y2,int c)
{
    b[x1][y1]+=c;
    b[x1][y2+1]-=c;
    b[x2+1][y1]-=c;
    b[x2+1][y2+1]+=c;
}
int main()
{
    int i,j;
    scanf("%d%d%d",&n,&m,&q);
    for(i=1;i<=n;i++)
        for(j=1;j<=m;j++)
            scanf("%d",&a[i][j]);
    for(i=1;i<=n;i++)
        for(j=1;j<=m;j++)
            insert(i,j,i,j,a[i][j]);
    while(q--)
    {
        int x1,y1,x2,y2,c;
        scanf("%d%d%d%d%d",&x1,&y1,&x2,&y2,&c);
        insert(x1,y1,x2,y2,c);
    }
    for(i=1;i<=n;i++)
        for(j=1;j<=m;j++)
            a[i][j]=a[i-1][j]+a[i][j-1]-a[i-1][j-1]+b[i][j];
    for(i=1;i<=n;i++)
    {
        for(j=1;j<=m;j++)
            cout<<a[i][j]<<" ";
        cout<<endl;
    }
    return 0;
}

（三）线段树

1.油漆面积

X星球的一批考古机器人正在一片废墟上考古。

该区域的地面坚硬如石、平整如镜。

管理人员为方便，建立了标准的直角坐标系。

每个机器人都各有特长、身怀绝技。

它们感兴趣的内容也不相同。

经过各种测量，每个机器人都会报告一个或多个矩形区域，作为优先考古的区域。

矩形的表示格式为 (x1,y1,x2,y2)，代表矩形的两个对角点坐标。

为了醒目，总部要求对所有机器人选中的矩形区域涂黄色油漆。

小明并不需要当油漆工，只是他需要计算一下，一共要耗费多少油漆。

其实这也不难，只要算出所有矩形覆盖的区域一共有多大面积就可以了。

注意，各个矩形间可能重叠。

输入格式

第一行，一个整数 n，表示有多少个矩形。

接下来的 n行，每行有 4 个整数 x1,y1,x2,y2，空格分开，表示矩形的两个对角顶点坐标。

输出格式

一行一个整数，表示矩形覆盖的总面积。

数据范围

1≤n≤10000
0≤x1,x2,y2,y2≤10000
数据保证 x1<x2 且 y1<y2。

输入样例1：

3
1 5 10 10
3 1 20 20
2 7 15 17

输出样例1：

340

输入样例2：

3
5 2 10 6
2 7 12 10
8 1 15 15

输出样例2：

128

代码：
题解稍后补上

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=10010;
int n;
struct Segment
{
    int x,y1,y2;
    int k;
    bool operator< (const Segment &t)const
    {
        return x<t.x;
    }
}seg[N*2];
struct node
{
    int l,r;
    int len,cnt;
}tr[N*4];
void pushup(int u)
{
    if(tr[u].cnt>0)
        tr[u].len=tr[u].r-tr[u].l+1;
    else if(tr[u].l==tr[u].r)
        tr[u].len=0;
    else
        tr[u].len=tr[u<<1].len+tr[u<<1|1].len;
}
void build(int u,int l,int r)
{
    tr[u]={l,r};
    if(l==r)
        return;
    int mid=l+r>>1;
    build(u<<1,l,mid),build(u<<1|1,mid+1,r);
}
void modify(int u,int l,int r,int k)
{
    if(tr[u].l>=l&&tr[u].r<=r)
    {
        tr[u].cnt+=k;
        pushup(u);
    }
    else
    {
        int mid=tr[u].l+tr[u].r>>1;
        if(l<=mid)
            modify(u<<1,l,r,k);
        if(r>mid)
            modify(u<<1|1,l,r,k);
        pushup(u);
    }
}
int main()
{
    cin>>n;
    int m=0;
    for(int i=0;i<n;i++)
    {
        int x1,y1,x2,y2;
        cin>>x1>>y1>>x2>>y2;
        seg[m++]={x1,y1,y2,1};
        seg[m++]={x2,y1,y2,-1};
    }
    sort(seg,seg+m);
    build(1,0,10000);
    int res=0;
    for(int i=0;i<m;i++)
    {
        if(i>0)
            res+=tr[1].len*(seg[i].x-seg[i-1].x);
        modify(1,seg[i].y1,seg[i].y2-1,seg[i].k);
    }
    printf("%d",res);
    return 0;
}