Prim
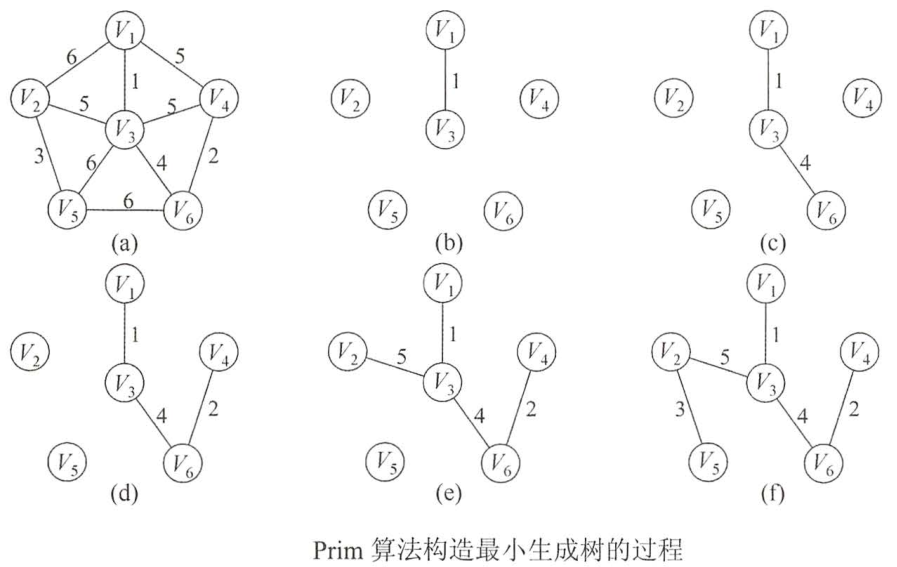
该算法的基本思想是从一个结点开始,不断加点,每次要选择距离最小的一个结点,以及用新的边更新其他结点的距离。
Dijkstra 算法一样,每次找到'距离最小'的一个点
Kruskal
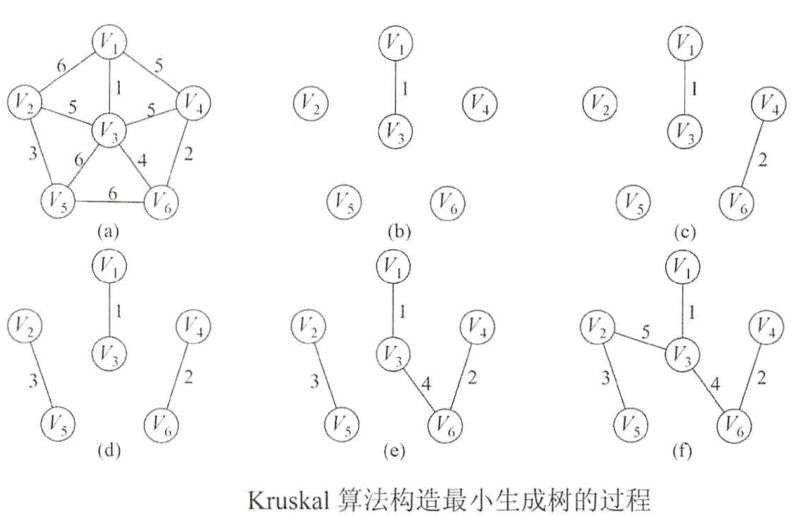
该算法的基本思想是'从小到大'加入边,我们从最小边权的边开始,按'边权从小到大依次加入',
如果某次加边产生了环,就扔掉这条边,直到加入了'n-1'条边,即形成了一棵树
Dijkstra
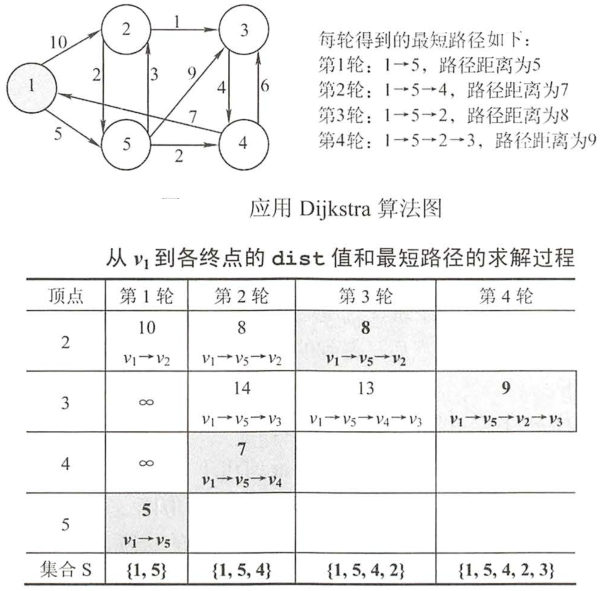
设置一个集合S记录已求得的最短路径的顶点,初始时把源点V0放入S,集合S每并入一个新顶点Vi,都要
修改源点V0到集合V-S中顶点当前的最短路径长度值。
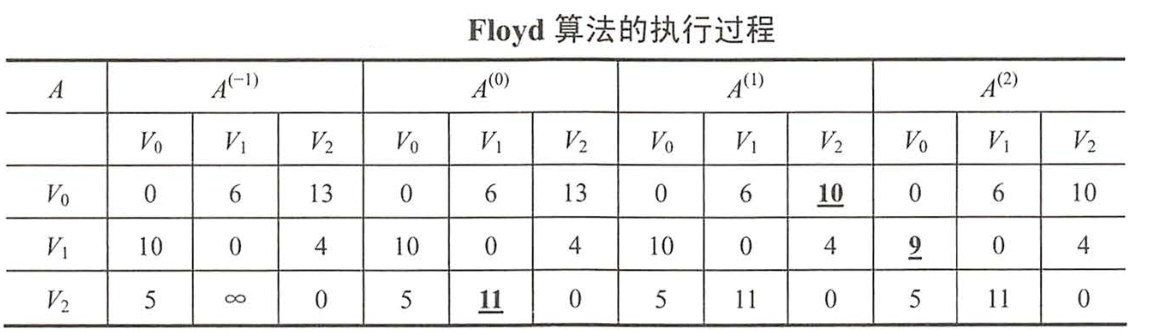
Floyd
用于求'各顶点'之间的"最短路径'问题
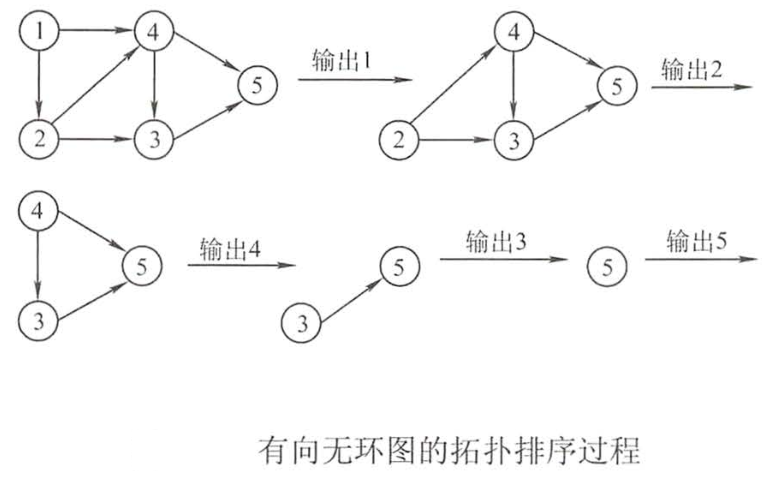
拓扑排序--AOV网
AOV:
①从AOV网中选择一个'没有前驱'的顶点并输出
②从网中删除该顶点和所有以'它为起点'的有向边
关键路径--AOE网
AOE:
①只有在某顶点所代表的时间'发生后',从该顶点出发的各有向边所代表的活动'才能开始'。
②只有进入某顶点的各有向边所代表的活动'都已结束'时,该顶点所代表的事件'才能发生'。
'关键路径'的活动都完成后,整个工程才能完成
可通过加快'关键活动'来'缩短工程的工期'; 网中的关键路径并不唯一,'只提高一条'关键路径上的关键活动
速度'并不能缩短整个工期'
