伪同行间:
虽然都是从事计算机,虽然都是从事互联网,虽然都是写代码的,(据说)写JAVA的瞧不起写JavaScript的,写JavaScript的瞧不起写CSS的。这可以理解,虽然养鸡养鸭成为富翁的不在少数,但是,一说你是农村养鸡的,怎么样?上海专业的丈母娘们的视线立马下降60°——被BS了。倒不是因为你是干农业的,而是“鸡”的问题;如果说你是饲养斯里兰卡蓝孔雀的,得,挑剔的丈母娘们说不定就会正脸看看(唷,斯里兰卡,国外货;唷,孔雀,高档货)。
同样的,如果你掌握的CSS都是些“砌砖头”的活(虽然砌砖头也是大学问),被无视也情理之中。但是,矩阵这个东西,就是扭转乾坤(网称“逆袭”)的好东西:CSS中也是有复杂的高档货的。再忽悠些“图形算法、位置计算”之类的词句,嘿嘿,立马看法从 变成
变成 。
。
二、何为矩阵?
矩阵可以理解为方阵,只不过,平时方阵里面站的是人,矩阵中是数值: →
→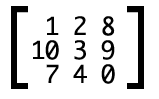
而所谓矩阵的计算,就是两个方阵的人(可以想象成古代的方阵士兵)相互冲杀。
CSS3中的矩阵
CSS3中的矩阵指的是一个方法,书写为matrix()和matrix3d(),前者是元素2D平面的移动变换(transform),后者则是3D变换。2D变换矩阵为3*3, 如上面矩阵示意图;3D变换则是4*4的矩阵。
有些迷糊?恩,我也觉得上面讲述有些不合时宜。那好,我们先看看其他东西,层层渐进——transform属性。
具体关于transform属性具体内容可以点击这里补个课。稍微熟悉的人都知道,transform中有这么几个属性方法:
.trans_skew { transform: skew(35deg); }
.trans_scale { transform:scale(1, 0.5); }
.trans_rotate { transform:rotate(45deg); }
.trans_translate { transform:translate(10px, 20px); }
斜拉(skew),缩放(scale),旋转(rotate)以及位移(translate)。
那你有没有想过,为什么transform:rotate(45deg);会让元素旋转45°, 其后面运作的机理是什么呢?
下面这张图可以解释上面的疑问: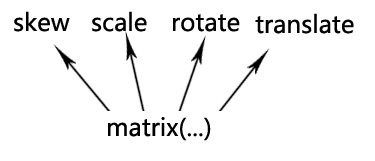
无论是旋转还是拉伸什么的,本质上都是应用的matrix()方法实现的(修改matrix()方法固定几个值),只是类似于transform:rotate这种表现形式,我们更容易理解,记忆与上手。
换句话说,理解transform中matrix()矩阵方法有利于透彻理解CSS3的transform属性,这就与那80%的也会应用但只知表象的人拉开了差距!
OK,现在上面提到的CSS3矩阵解释应该说得通了。
三、矩阵应用场景
虽然题目写的是“transform中的Matrix”,实际上,在CSS3以及HTML5的世界里,这玩意还是涉猎蛮广的,如SVG以及canvas.
事实上,关于矩阵,我之前曾经介绍过,是在介绍IE浏览器下的Matrix矩阵滤镜的时候说过,IE的滤镜矩阵与CSS中的矩阵虽然写法上差异较大,但是,矩阵计算的原来是一致的。只是之前的介绍主要是IE下的旋转与缩放,同时也不是很深入,因此还有有些局限的。
四、transform与坐标系统
用过transform旋转的人可以发现了,其默认是绕着中心点旋转的,而这个中心点就是transform-origin属性对应的点,也是所有矩阵计算的一个重要依据点(下图参考自dev.opera.com)。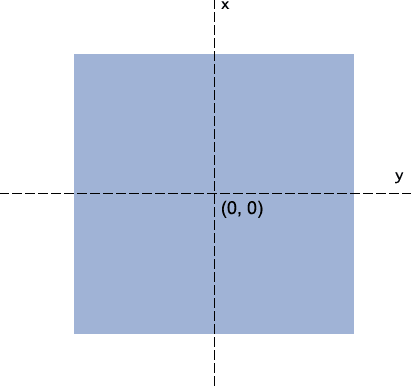
当我们通过transform-origin属性进行设置的时候,矩阵相关计算也随之发生改变。反应到实际图形效果上就是,旋转拉伸的中心点变了!
举例来说,如果偶们设置:
-webkit-transform-origin: bottom left;
则,坐标中心点就是左下角位置。于是动画(例如图片收缩)就是基于图片的左下角这一点了: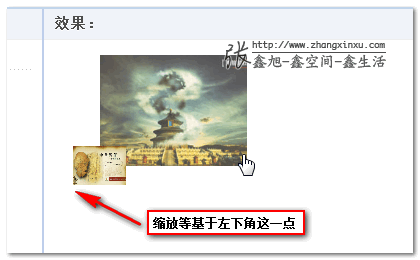
上图效果可以点击这里查看(Chrome浏览器)。
再举个稍微难理解的例子,我们如果这样设置:
transform-origin: 50px 70px;
则,中心点位置有中间移到了距离左侧50像素,顶部70像素的地方(参见下图),而此时的(30, 30)的坐标为白点所示的位置(这个位置后面会用到)。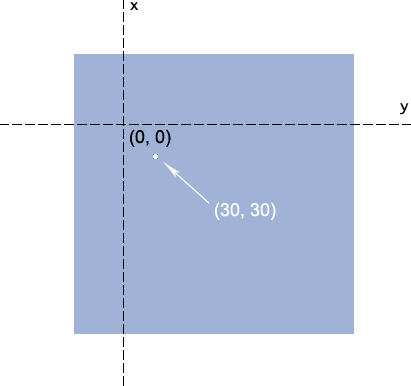
仔细看看,是不是很快就理解了哈~~
五、准备好了没?重头戏来了
CSS3 transform的matrix()方法写法如下:
transform: matrix(a,b,c,d,e,f);
吓住了吧,这多参数,一个巴掌都数不过来。好吧,如果你把a~f这6个参数想象成女神的名词,你会觉得,世界不过如此嘛~~
实际上,这6参数,对应的矩阵就是: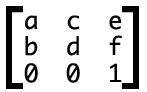
注意书写方向是竖着的。
上面提过,矩阵可以想象成古代的士兵方阵,要让其发生变化,只有与另外一个士兵阵火拼就可以了,即使这是个小阵。
反应在这里就是如下转换公式: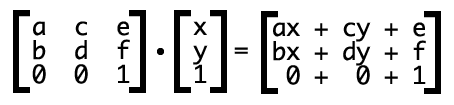
其中,x, y表示转换元素的所有坐标(变量)了。那后面的ax+cy+e怎么来的呢?
//zxx:大学时候线性代数知识,懂的人这里可以直接跳过
很简单,3*3矩阵每一行的第1个值与后面1*3的第1个值相乘,第2个值与第2个相乘,第3个与第3个,然后相加,如下图同色标注: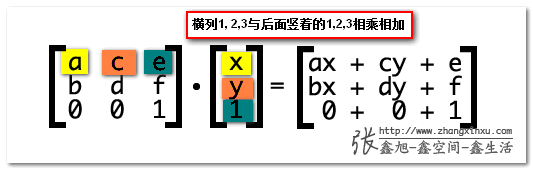
那ax+cy+e的意义是什么?
记住了,ax+cy+e为变换后的水平坐标,bx+dy+f表示变换后的垂直位置。
又迷糊了?不急,一个简单例子就明白了。
假设矩阵参数如下:
transform: matrix(1, 0, 0, 1, 30, 30); /* a=1, b=0, c=0, d=1, e=30, f=30 */
现在,我们根据这个矩阵偏移元素的中心点,假设是(0, 0),即x=0, y=0。
于是,变换后的x坐标就是ax+cy+e = 1*0+0*0+30 =30, y坐标就是bx+dy+f = 0*0+1*0+30 =30.
于是,中心点坐标从(0, 0)变成了→(30, 30)。对照上面有个(30, 30)的白点图,好好想象下,原来(0,0)的位置,移到了白点的(30, 30)处,怎么样,是不是往右下方同时偏移了30像素哈!!
实际上transform: matrix(1, 0, 0, 1, 30, 30);就等同于transform: translate(30px, 30px);. 注意:translate, rotate等方法都是需要单位的,而matrix方法e, f参数的单位可以省略。
一例胜万语,您可以狠狠地点击这里:matrix(1,0,0,1,30,30)实例demo
在现代浏览器下,会有类似下面动图的效果:
效果只是表象的,我想到了一个更好的idea去表现矩阵到底是如何变换的,您可以狠狠地点击这里:matrix分解变换演示
为了提高性能,demo中每个单元分解成了5px * 5px的区域。演示分两步,先是演示每个单元的位置是如何计算的,接着动画表现其位置的偏移。
这个demo所做的工作就是把浏览器瞬间完成的计算和渲染变成了可控的分步显示,这样,大家就可以很直观地看出,这个矩阵计算到底是如何起作用的。下图为正在演示过程中的截图: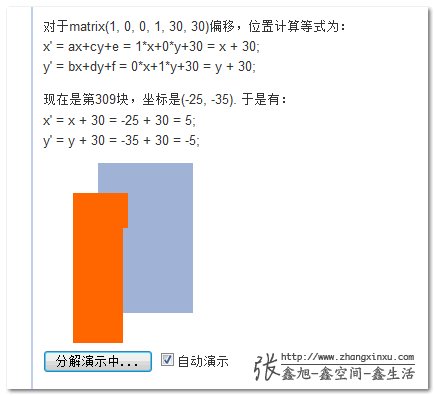
//zxx:由于默认100毫秒间隔不断渲染,因此如果你电脑CPU或是浏览器hold不住,可以取消“自动演示”的勾选,然后,点击左边的按钮手动分步查看。
总结
聪明的你可能以及意识到了,尼玛matrix表现偏移就是:
transform: matrix(与我无关, 哪位, 怎么不去高考, 打麻将去吧,水平偏移距离, 垂直偏移距离);
你只要关心后面两个参数就可以了,至于前面4个参数,是牛是马,是男是女都没有关系的。
六、transform matrix矩阵与缩放,旋转以及拉伸
偏移是matrix效果中最简单,最容易理解的,因此,上面很详尽地对此进行展开说明。下面,为了进一步加深对matrix的理解,会简单讲下matrix矩阵与缩放,旋转以及拉伸效果。
缩放(scale)
上面的偏移只要关心最后两个参数,这个缩放也是只要关心两个参数。哪两个呢?
如果你足够明察秋毫,应该已经知道了,因为上面多次出现的:
transform: matrix(1, 0, 0, 1, 30, 30);
已经出卖了。
发现没,matrix(1, 0, 0, 1, 的元素比例与原来一样,1:1, 而这几个参数中,有两个30, 30);1, 啊哈哈!没错,这两个1就是缩放相关的参数。
其中,第一个缩放x轴,第二个缩放y轴。
用公式就很明白了,假设比例是s,则有matrix(s, 0, 0, s, 0, 0);,于是,套用公式,就有:x' = ax+cy+e = s*x+0*y+0 = s*x;y' = bx+dy+f = 0*x+s*y+0 = s*y;
也就是matrix(sx, 0, 0, sy, 0, 0);,等同于scale(sx, sy);
好了,至此,无需多说了……
眼见为实,因此demo还是要滴,您可以狠狠地点击这里:matrix矩阵与缩放demo
为了避免元素比例放大时候遮盖上面的文本框以及描述位子,因此,将元素的坐标原点迁至了左上角。

旋转(rotate)
旋转相比前面两个要更高级些,要用到(可能勾起学生时代阴影的)三角函数。
方法以及参数使用如下(假设角度为θ):
matrix(cosθ,sinθ,-sinθ,cosθ,0,0)
结合矩阵公式,就有:
x' = x*cosθ-y*sinθ+0 = x*cosθ-y*sinθ y' = x*sinθ+y*cosθ+0 = x*sinθ+y*cosθ
这个与IEMatrix滤镜中的旋转是有些类似的(M11表示矩阵第1行第1个(参数a),M21表示矩阵第2行第一个(参数b)……):
filter:progid:DXImageTransform.Microsoft.Matrix(M11=cosθ,M21=sinθ,M12=-sinθ,M22=cosθ');
哎呀呀,四个参数,我记不住啊!莫慌,我们可以这样子记忆:
CS-SC:初三-上床,对称结构,这下忘不了了吧~~
您可以狠狠地点击这里:transform matrix矩阵与旋转demo

不过,说句老实话,就旋转而言,rotate(θdeg)这种书写形式要比matrix简单多了,首先记忆简单,其次,无需计算。例如,旋转30°,前者直接:
transform:rotate(30deg);
而使用matrix表示则还要计算cos, sin值:
transform: matrix(0.866025,0.500000,-0.500000,0.866025,0,0);
拉伸(skew)
拉伸也用到了三角函数,不过是tanθ,而且,其至于b, c两个参数相关,书写如下(注意y轴倾斜角度在前):
matrix(1,tan(θy),tan(θx),1,0,0)
套用矩阵公式计算结果为:
x' = x+y*tan(θx)+0 = x+y*tan(θx) y' = x*tan(θy)+y+0 = x*tan(θy)+y
对应于skew(θx + "deg",θy+ "deg")这种写法。
其中,θx表示x轴倾斜的角度,θy表示y轴,两者并无关联。
还是靠实例说话吧,您可以狠狠地点击这里:matrix矩阵与拉伸demo
在Chrome下可以很动态地查看不同倾斜角度对应的拉伸的效果:
七、既然有简单的skew, rotate..,那matrix有何用?
我想有人会奇怪,既然CSS3 transform中提供了像skew, rotate, …效果,那还需要掌握和熟悉让人头大的矩阵方法干嘛呢?
好问题,确实,对于一般地交互应用,transform属性默认提供的些方法是足够了,但是,一些其他的效果,如果transform属性没有提供接口方法,那你又该怎么办呢?比方说,“镜像对称效果”!
没辙了吧,这是,就只能靠matrix矩阵了。要知道,matrix矩阵是transform变换的基础,可以应付很多高端的效果,算是一种高级应用技巧吧。掌握了基础,才能兵来将挡水来土掩啊。
OK,这里就演示下,如何使用CSS3 transform matrix矩阵实现镜像效果。
这个有点难度,因此,我们先看demo,您可以狠狠地点击这里:matrix与镜像对称效果demo
框框中输入旋转的角度值(用来确定镜像的对称轴),然后失去焦点,就会呈现出对应的镜像对称效果了:
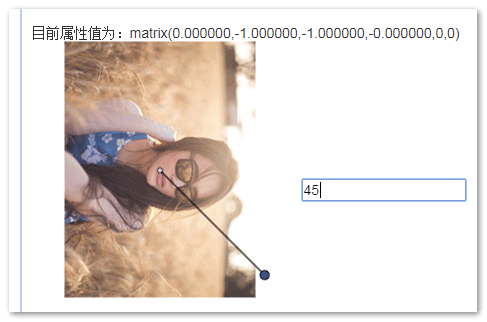
您可以在FireFox或是Chrome等浏览器上体验下matrix实现的镜像渐变效果。
demo页面中的一个轴是为了便于理解我加上的效果,实际上,在镜像对称的时候轴是看不见的。
轴围绕的那个点就是CSS3中transform变换的中心点,自然,镜像对称也不例外。因为该轴永远经过原点,因此,任意对称轴都可以用y = k * x表示。则matrix表示就是:
matrix((1-k*k) / (1+k*k), 2k / (1 + k*k), 2k / (1 + k*k), (k*k - 1) / (1+k*k), 0, 0)
这个如何得到的呢?
啊,高中数学来了,就当再高考一次吧,如下图,已经y=kx,并且知道点(x, y)坐标,求其对称点(x’, y’)的坐标?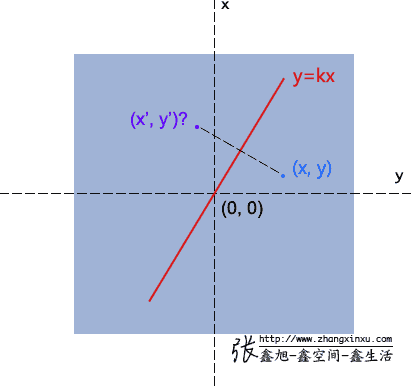
很简单,一是垂直,二是中心点在轴线上,因此有:
(y-y') / (x - x') = -1/ k → ky-ky' = -x+x'(x + x') / 2 * k = (y + y')/2 → kx+kx' = y+y'
很简单的,把x'和y'提出来,就有:
x' = (1-k*k)/(k*k+1) *x + 2k/(k*k+1) *y;y' = 2k/(k*k+1) *x + (k*k-1)/(k*k+1) *y;
再结合矩阵公式:x' = ax+cy+e;y' = bx+dy+f;
我们就可以得到:a = (1-k*k)/(k*k+1);b = 2k/(k*k+1);c = 2k/(k*k+1);d = (k*k-1)/(k*k+1);
也就是上面matrix方法中的参数值啦!
下图为自己计算的草稿:
八、3D变换中的矩阵
3D变换虽然只比2D多了一个D,但是复杂程度不只多了一个。从二维到三维,是从4到9;而在矩阵里头是从3*3变成4*4, 9到16了。
其实,本质上很多东西都与2D一致的,只是复杂度不一样而已。这里就举一个简单的3D缩放变换的例子。
对于3D缩放效果,其矩阵如下: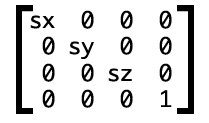
代码表示就是:
transform: matrix3d(sx, 0, 0, 0, 0, sy, 0, 0, 0, 0, sz, 0, 0, 0, 0, 1)