根据三个坐标点以及三个坐标点的半径( x1 , y1 ) , d1 , ( x2 , y2 ) , d2 , ( x3 , y3 ) , d3,即可求得三个点的交点 ( x0 , y0 ) 。
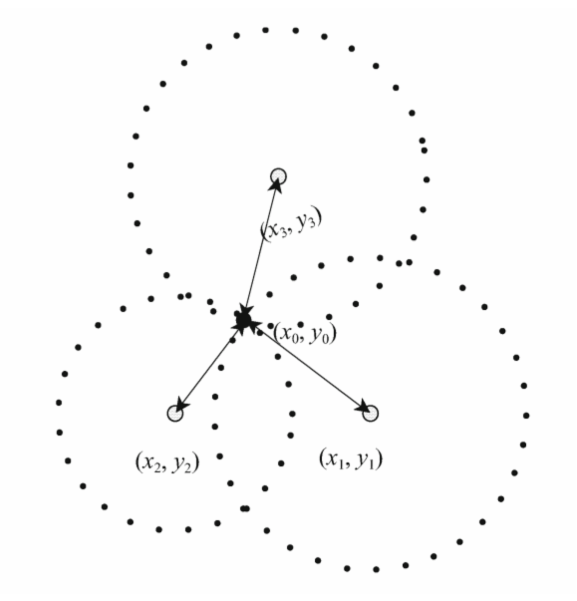
通过勾股定理可得出:
Math.power((x1 - x0), 2) + Math.power((y1 - y0), 2) = Math.power(d1, 2); Math.power((x2 - x0), 2) + Math.power((y2 - y0), 2) = Math.power(d2, 2); Math.power((x3 - x0), 2) + Math.power((y3 - y0), 2) = Math.power(d3, 2);
再次通过分解因式可获得( x0 , y0 ):
function position(x1, x2, x3, y1, y2, y3, d1, d2, d3) {
var x0 = ((Math.pow(d1, 2) - Math.pow(d3, 2) + Math.pow(x3, 2) - Math.pow(x1, 2) + Math.pow(y3, 2) - Math.pow(y1, 2)) * (y2 - y1) - (Math.pow(d1, 2) - Math.pow(d2, 2) + Math.pow(x2, 2) - Math.pow(x1, 2) + Math.pow(y2, 2) - Math.pow(y1, 2)) * (y3 - y1)) / (2 * (x3 - x1) * (y2 - y1) - 2 * (x2 - x1) * (y3 - y1)) var y0 = ((Math.pow(d1, 2) - Math.pow(d3, 2) + Math.pow(x3, 2) - Math.pow(x1, 2) + Math.pow(y3, 2) - Math.pow(y1, 2)) * (x2 - x1) - (Math.pow(d1, 2) - Math.pow(d2, 2) + Math.pow(x2, 2) - Math.pow(x1, 2) + Math.pow(y2, 2) - Math.pow(y1, 2)) * (x3 - x1)) / (2 * (y3 - y1) * (x2 - x1) - 2 * (y2 - y1) * (x3 - x1)) return { x0: x0, y0: y0 } }